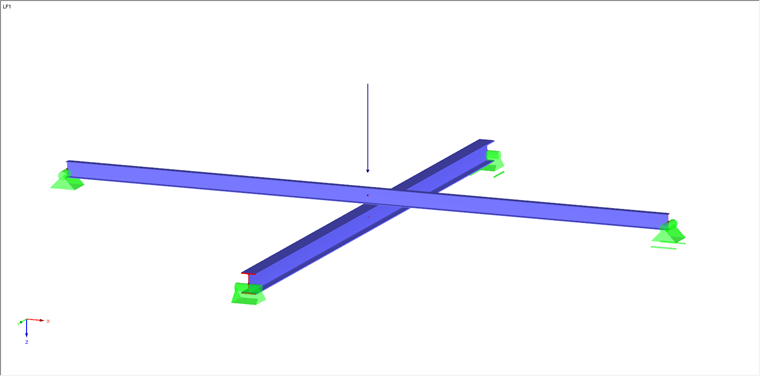
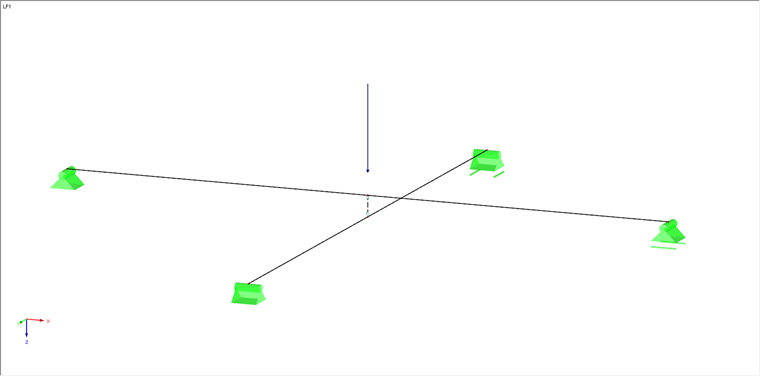
Zur Realisierung der zuvor beschriebenen Situation empfiehlt sich zunächst eine Teilung der beiden Stäbe auf Höhe der Kreuzung, sodass an diesen Stellen jeweils ein neuer Knoten entsteht. Falls die Funktion "Linien/Stäbe verbinden" im Kontextmenü deaktiviert ist, ist sie manuell bei den beiden kreuzenden Stäben anzuwenden. Diese werden daraufhin jeweils am zuvor eingefügten Knoten geteilt, sind aber nach wie vor ein jeweils durchlaufender Stab.
Im nächsten Schritt werden die beiden kreuzenden Stäbe zwischen den beiden neuen Knoten durch einen kurzen Starrstab miteinander verbunden.
Der Starrstab erhält idealerweise am Stabanfang sowie am Stabende jeweils ein Momentengelenk, sodass an dieser Stelle keine Momente übertragen werden.
Im letzten Schritt sind an der Verbindung beziehungsweise am eingefügten Starrstab die folgenden zwei Bedingungen zu definieren:
- Ausfall bei Zug, sprich bei abhebendem oberen Stab
- Kraftübertragung bei Druck erst bei Kontakt der beiden Stäbe
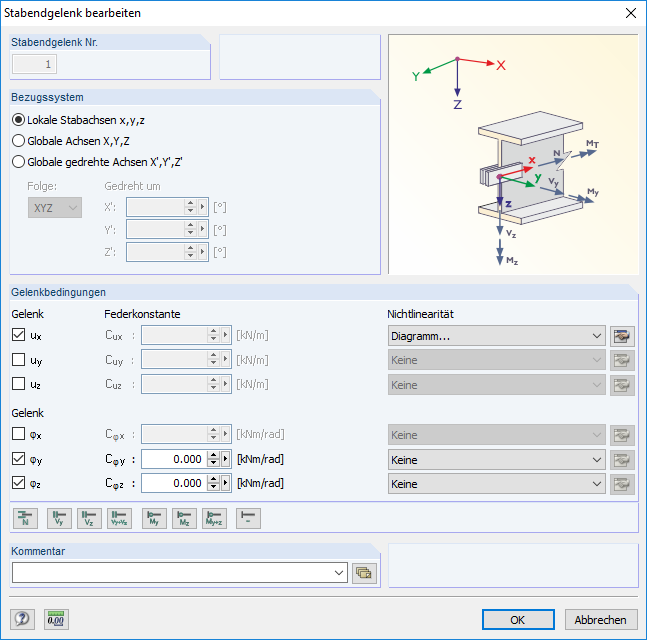
Beide Bedingungen können an einem der beiden Stabendgelenke des Starrstabes als Nichtlinearität per Diagramm definiert werden. Dazu ist zunächst das Dialogfenster "Stabendgelenk bearbeiten" aufzurufen.
Nachdem als Bezugssystem die lokalen Stabachsen ausgewählt sind und dementsprechend das Normalkraftgelenk ux aktiviert ist, kann rechts daneben das Diagramm als Nichtlinearität ausgewählt werden. Per Schaltfläche "Nichtlinearität des Normalkraft-Gelenkes N bearbeiten" wird nun das Dialogfenster "Nichtlinearität - Diagramm - Stabendgelenk ux" aufgerufen.
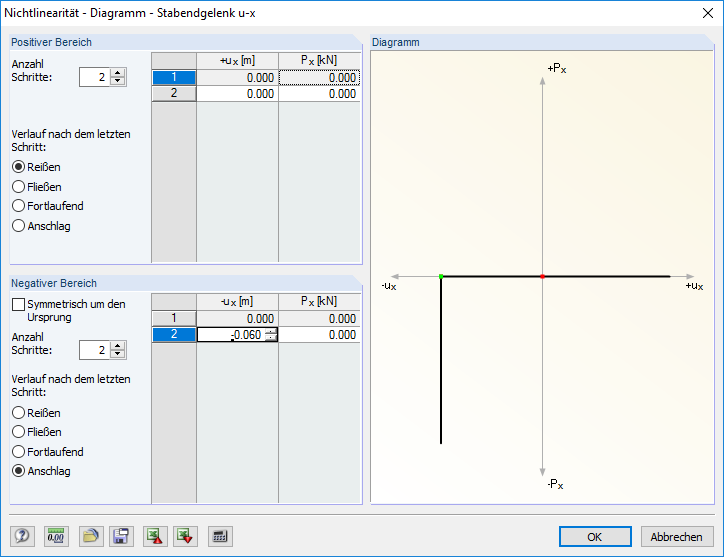
Im positiven Bereich der Normalkraft wird der Ausfall bei Zug definiert. Das heißt: Hier wird lediglich die Option "Reißen" (nach dem letzten Schritt) aktiviert. Im negativen Bereich der Normalkraft wird zuerst die Option "Symmetrisch um den Ursprung" deaktiviert, sodass die folgenden zwei Schritte definiert werden können:
Die zuvor genannten 6 cm "Schlupf" sind der Abstand zwischen Oberkante des unteren Trägers und Unterkante des oberen Trägers und gelten natürlich nur für dieses Beispiel. Diese sind also je nach Abstand der beiden Träger anzupassen. Der entsprechende Betrag wird wie folgt ermittelt:
ux = (Länge des Starrstabes) - (halbe Trägerhöhe oberer Stab) - (halbe Trägerhöhe unterer Stab)
Damit die Kraft nach dem Erreichen der definierten Verformung voll wirkt, ist als Verlauf nach dem letzten Schritt "Anschlag" zu wählen. Die Dialogfenster können nun beide nacheinander mit [OK] bestätigt werden.
Grafische und numerische Kontrolle
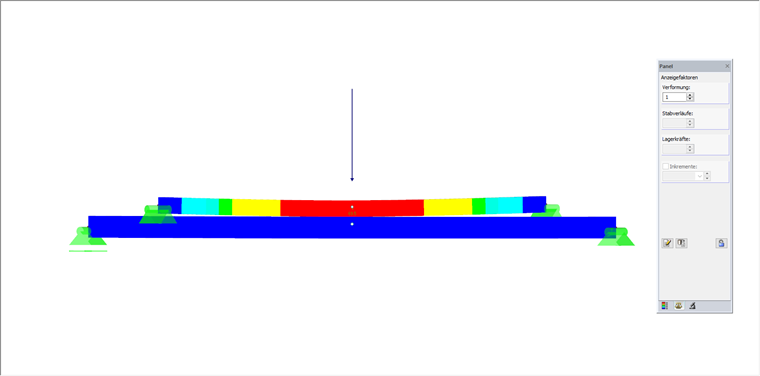
Nachdem die Nichtlinearität erfolgreich definiert und die ersten Ergebnisse erzielt wurden, ist bei Betrachtung der Verformungen deren Überhöhungsfaktor zu beachten (siehe Panel, Register "Faktoren", "Anzeigefaktor für Verformung"). Eine grafische Kontrolle der definierten Nichtlinearität ist bei möglichem Kontakt der Stäbe (Druck) nur mit dem Anzeigefaktor "1" sinnvoll, da es bei überhöhter Darstellung der Verformung beispielsweise so aussieht, als biege sich der obere Stab weiter herunter als der untere Stab.
Bezogen auf die eigene Ursprungslage ist die Durchbiegung des oberen Stabes bei Kontakt der Stäbe natürlich zwangsläufig immer größer als die Durchbiegung des unteren Stabes. Desweiteren sollten neben der grafischen Kontrolle auch die Verformungswerte überprüft werden, um sicher zu stellen, dass die entsprechende Nichtlinearität korrekt definiert wurde. Bei Kontakt der beiden Stäbe gilt dann:
(Verformung des oberen Stabes) - (Betrag des definierten Schlupfes ux) = (Verformung des unteren Stabes)
Ebenfalls sollte der Starrstab bei Kontakt der beiden Träger eine entsprechende Drucknormalkraft erhalten. Die diesbezügliche Option ist im Zeigen-Navigator zu aktivieren (siehe FAQ 002080).
