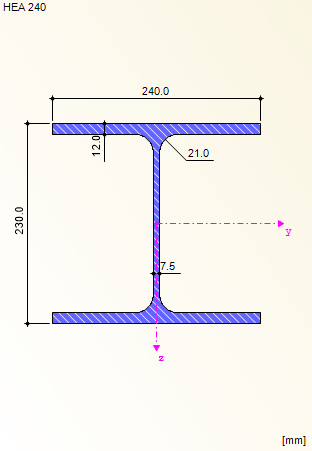
Nachweis der Querschnittsklasse
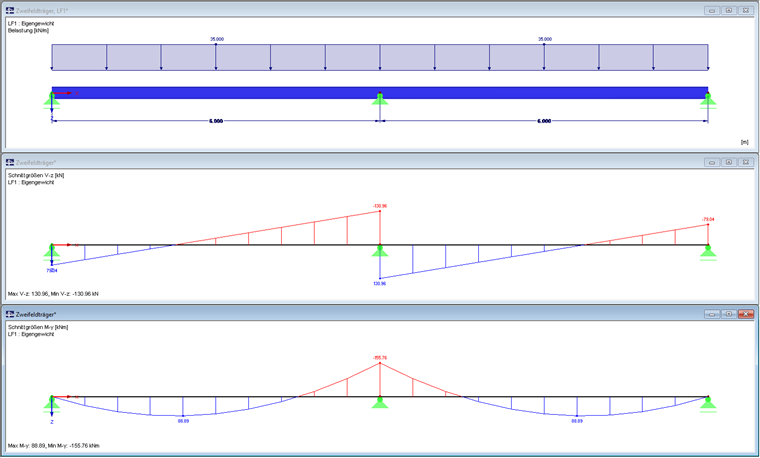
Für den Nachweis der Querschnittsklasse sowie für den zu führenden Querschnittsnachweis ist der Bereich des Innenlagers des Zweifeldträgers maßgebend.
Nachweis für den Steg (ψ = -1)
[1] Tabelle 5.2, zweiseitig gestützte Querschnittsteile
Somit erfüllt der Steg die Anforderungen an die Querschnittsklasse 1.
Nachweis für den Untergurt (ψ = 1)
[1] Tabelle 5.2, einseitig gestützte Querschnittsteile
Die Gurte erfüllen demnach die Anforderungen der Querschnittsklasse 2. Der Querschnitt ist der Querschnittsklasse 2 zuzuordnen, da die Klasse des am ungünstigsten bewerteten Querschnittsteils für den gesamten Querschnitt maßgebend wird.
Schubbeulen des Steges
Ob das Schubbeulen des Steges zu berücksichtigen ist, ist unabhängig von der Zuordnung der Querschnittsklasse nach Abschnitt 6.2.6, Absatz (6) in [1] zu überprüfen. Der Wert η in der Gleichung 6.22 in [1] wird mit 1,20 angesetzt.
Nach DIN EN 1993-1-5, Abschnitt 5 muss kein Schubbeulnachweis geführt werden.
Querkraftnachweise
Für den Querschnitt der Klasse 2 wird der Querschnittsnachweis geführt. Über dem Innenlager wird der Träger auf Biegung und Querkraft beansprucht, an der Stelle des maximalen Feldmomentes nur auf Biegung. Der Einfluss der M-V-Interaktion wird vor der Ermittlung der Systemtragfähigkeit geprüft. Wenn VEd nicht mehr als 0,5 ⋅ Vpl,Rd beträgt, muss keine Abminderung der Momententragfähigkeit nach [1] Absatz 6.2.8 (2) erfolgen.
Eine Abminderung der Momententragfähigkeit ist nicht erforderlich.
Für den Bemessungswert der einwirkenden Biegemomente MEd ist folgender Nachweis zu erfüllen:
Der Bemessungswert der Biegebeanspruchbarkeit eines mit einachsiger Biegung belasteten Querschnitts wird für Querschnitte der Klasse 2 wie folgt ermittelt:
Dlubal_KohlA_]_LI.jpg?mw=350&hash=21d94ec9a723c608496e9e95a21bb1309ab5067a)
www.isen_LI.jpg?mw=350&hash=884ca7c4739fd5d2643994f417a345f17b1e1fad)
.png?mw=350&hash=2b12ead9717e0abbf1c0c14bba66b0a2adcaed73)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
