Für das allgemeine Beispiel in diesem Artikel wird eine 3D-Holzstruktur verwendet, die ein gekrümmtes Holzdach hat, das sich bis zum Fundament erstreckt. Die freie Spannweite eines einzelnen Holzbogens beträgt 20 m und die Höhe von der Basis bis zur Krone des Bogens beträgt 5 m.
.png?mw=760&hash=98b2f1246383943431fc6a42aea24106d857b661)
Schneelasten aus ASCE 7-16
Abbildung 7.4-2 [1] in der Norm zeigt, wie ein gekrümmtes Dach sowohl für symmetrische als auch für unsymmetrische Schneelasten belastet wird. Die Aufbringung der Schneelast nach unten variiert entlang der Bogenlänge in Abhängigkeit von der Dachneigung an einer bestimmten Stelle. Daher ist es notwendig, die Neigung in Grad über die gesamte Bogenlänge zu bestimmen.
Ermittlung der Dachneigung
Wenn man die Seitenansicht des Bogendachs in ein einfaches Linienelement umwandelt und auf ein x- und y-Koordinatensystem projiziert, werden die x-Koordinatenpunkte mit einer Steigung von 0,30 m entlang des Fundaments der Struktur bestimmt. Da der Bogen aus dem Modellbeispiel nur ein Teil eines größeren Kreises ist, kann die Gleichung für einen Kreis verwendet werden, um zusätzliche Informationen über die Bogenlänge zu ermitteln.
| x | Koordinate eines Bogens entlang der x-Achse |
| y | Koordinate eines Bogens entlang der y-Achse |
| h | x-Koordinate des Kreismittelpunktes |
| k | y-Koordinate des Kreismittelpunktes |
| r | Radius oder Kreis |
Dabei ist
x = Koordinate des Bogens entlang der x-Achse
y = Koordinate des Bogens entlang der y-Achse
h = x-Koordinate des Kreismittelpunktes
k = y-Koordinate des Kreismittelpunktes
r = Radius oder Kreis
Wenn man die obige Gleichung umstellt, da alle Werte außer der y-Koordinate des Bogens angegeben sind, lautet die Gleichung:
Um die Neigung eines Punktes irgendwo entlang des Bogens zu finden, muss die Gleichung des Kreises in Bezug auf x implizit differenziert werden.
Durch Lösen der impliziten Differenzierung ergibt sich folgender Anstieg/ Lauf der Steigung, der mit dx/dy bezeichnet wird.
Um die Neigung in Grad zu bestimmen, wird die Umkehrfunktion zur Tangensfunktion angewendet.
Zusätzlich kann die obige Gleichung für "y" in die Neigungsgleichung eingesetzt werden, da dieser Wert beim Vergleich mit dem bekannten x-Koordinatenpunkt möglicherweise nicht ohne weiteres bekannt ist. Es ist jetzt möglich, die Neigung in Grad entlang jeder x-Position für den Strukturbogen zu bestimmen.
Schneelastgröße
Nach Abb. 7.4-2 gibt es drei verschiedene Fälle, die von der gekrümmten Dachgeometrie an der Dachkante oder Traufe abhängig sind.
- Bogenneigung an der Traufe < 30°
- Bogenneigung an der Traufe 30 ° bis 70 °
- Bogenneigung an der Traufe > 70°
Für jeden Fall wird sowohl eine symmetrische als auch eine unsymmetrische Belastung entlang der Bogenlänge angegeben. Die Schneelast, die auf eine geneigte Fläche einwirkt, wird in der horizontalen Projektion der Fläche aufgebracht. Abb. 7.4-2 fasst diese Lastwerte zusammen, indem die Schneelast pf des Flachdachs mit dem Dachneigungsfaktor Cs multipliziert wird. Cs berücksichtigt die unterschiedliche Neigung entlang der Bogenlänge und hängt von mehreren Faktoren ab, die in Abbildung 7.4-1 [1] angegeben sind, einschließlich des Wärmefaktors Ct in Tabelle 7.3-2 [1], dem Flächentyp (d.h. hindernisfreie glatte Flächen im Vergleich zu allen anderen Flächentypen) und der Dachneigung in Grad, die oben in der Neigungsgleichung bestimmt wurde.
Der Expositionsfaktor Ce wird für die Schneelastgröße an Stellen benötigt, an denen die Bogenneigung zwischen 30° und 70° variiert, wie in Abb. 7.4-2 nur für unsymmetrische Lastszenarien dargestellt. Dieser Wert kann in Abhängigkeit von der Geländekategorie und der Bedingung der Dachausrichtung aus Tabelle 7.3-1 [1] ermittelt werden.
Die Schneelast des Flachdaches wird aus der nachfolgend angegebenen Gleichung 7.3-1 [1] ermittelt.
pf = 0,7 ⋅ Ce ⋅ Ct ⋅ Is ⋅ pg
Ce und Ct wurden oben erläutert und sind in Tabelle 7.3-1 bzw. 7.3-2 zu finden. Der Wichtigkeitsfaktor Is ist in Tabelle 1.5-2 [1] zu finden, der wiederum von der Risikokategorie aus Tabelle 1.5-1 [1] abhängt. Die Bodenschneelast pg ist in Abb. 7.2-1 [1] und Tabelle 7.2-1 [1] angegeben.
Dlubal Software hat die direkt in ASCE 7-16 enthaltenen Karten zur Bodenschneelast in die Google Maps-Technologie integriert, um das Geo-Zone-Tool zu entwickeln, das auf der Dlubal-Website verfügbar ist. Mit diesem Tool kann der Benutzer die Adresse des Projektstandorts eingeben oder direkt auf die Karte klicken. Im Gegenzug zeigt das Geo-Zone-Tool automatisch die Schnee-, Wind- und Erdbebendaten an, die auf ASCE 7-16 für den angegebenen Standort basieren. Dies ist eine effizientere und einfachere Alternative zur Bestimmung der Schneelasten für verschiedene Standorte in den USA im Vergleich zur manuellen Suche dieser Informationen in der Norm.
- Weitere Informationen zum Geo-Zonen-Tool für Schneelastzonen, Windzonen und Erdbebenzonen nach ASCE 7-16:
Schneelastort
Für alle drei Schneelastfälle für gekrümmte Dächer variiert die Größe entlang der Bogenlänge in Abhängigkeit von der Dachneigung, die in den Lastdiagrammen in Abb. 7.4-2 angegeben ist. Die wichtigsten Stellen, die für einen der drei Fälle benötigt werden, sind 70°, 30° und der First. Mit der oben genannten Neigungsgleichung können diese spezifischen Punkte leicht entlang der Bogenlänge bestimmt werden. Die Größen variieren linear zwischen diesen spezifischen Stellen, sodass es nicht erforderlich ist, die Schneelastgröße an jedem Neigungspunkt zu ermitteln.
Für die Szenarien mit symmetrischer Last wird die Größe des Bogens links und rechts vom First als Cs ⋅ pf festgelegt, wobei Cs = 1,0 ist. Daher muss man anhand von Abbildung 7.4-1 bestimmen, an welcher entsprechenden Stelle der Dachneigung der Cs-Faktor gleich 1,0 ist. Sobald diese Dachneigung bestimmt ist, kann der Punkt entlang der Bogenlänge basierend auf den Informationen aus der Neigungsgleichung ermittelt werden.
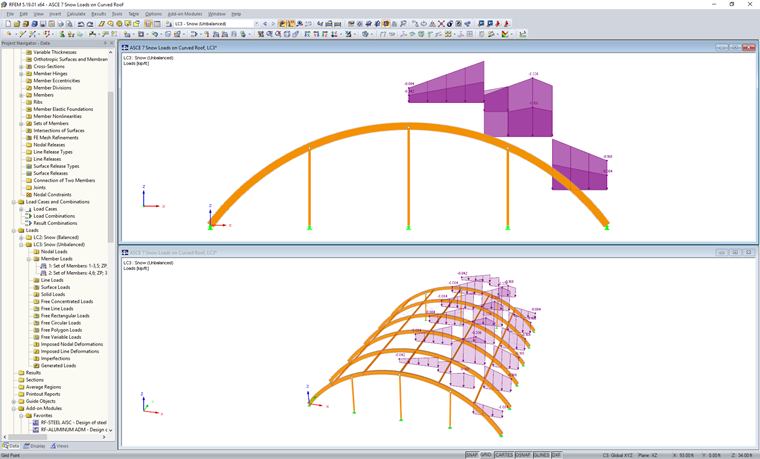
Bei unsymmetrischen Lastszenarien gilt die Luvseite als schneefrei. Die Schneelast wird nur entlang der Leeseite auf den Bogen aufgebracht, wie in den Lastdiagrammen angegeben. Wenn ein anderes Dach am betrachteten Dach angrenzt, wird in den Diagrammen auch angegeben, wie diese Sonderfälle in den unsymmetrischen Lastfällen sowohl für die Größe der Last als auch für die Positiont zu berücksichtigen sind.
Anwendung in RFEM
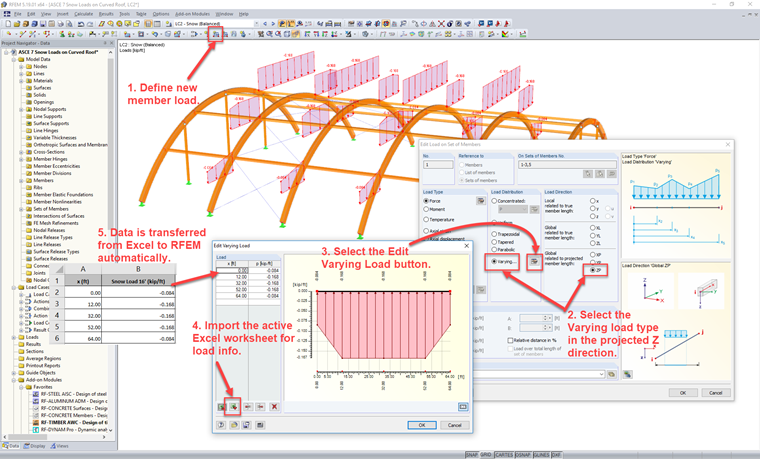
Komplexe Ladstzenarien lassen sich in RFEM mit den verfügbaren Werkzeugen einfach handhaben. Das wahrscheinlich einfachste Szenario für die Berechnung der Dachneigung an allen Stellen entlang der Bogenlänge, die durch die oben beschriebenen Anfangsgleichungen angegeben wird, ist die Verwendung eines Tabellenkalkulationsprogramms wie Microsoft Excel.
Mit der berechneten Dachneigung und den obigen Schritten zur Bestimmung der Schneelastgröße aus ASCE 7-16 können die Lasten in Excel auf einige extreme Stellen vereinfacht werden, wie z.B. 70°, 30° und Traufe. Diese Informationen können in Tabellenform in einem einzigen Arbeitsblatt festgelegt werden, wobei die x-Stelle entlang der projizierten x-Achse des Bogens und die entsprechende Größe der Schneelast definiert wird.
Wählen Sie in RFEM "Neue Stablast" aus, um es entweder auf Stäbe oder auf Stabsätze anzuwenden. Der "veränderliche" Lastverlauf wird in der projizierten Z-Richtung ZP verwendet. Um die Tabelle innerhalb des Programms zu aktivieren, ist die Schaltfläche "Veränderliche Last bearbeiten" zusätzlich auszuwählen. Mit einem Klick können alle aktuell im aktiven Excel-Arbeitsblatt definierten Informationen direkt in die RFEM-Tabelle importiert werden.
Das gleiche Szenario kann für einen separaten Lastfall in RFEM angewendet werden, um die unsymmetrische Schneelast anzuwenden.
Die Möglichkeit veränderliche Lasten direkt aus Excel zu importieren kann für das Aufbringen mehrerer Stablasten hilfreich sein, bei denen die Lastgröße entlang der Stablänge erheblich variiert.