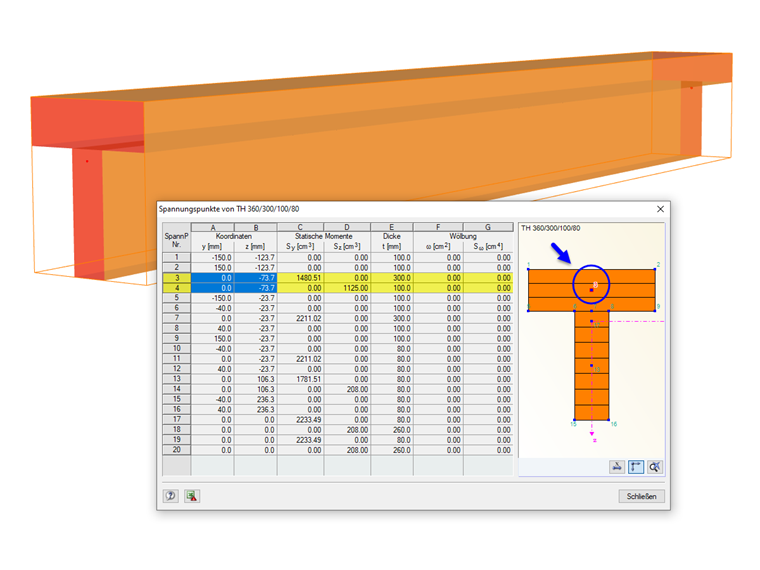
Spannungspunkt-Kennwerte
Zur Ermittlung der Spannungen werden folgende Kennwerte eines Spannungspunkts herangezogen:
- Koordinaten, bezogen auf den Schwerpunkt des Querschnitts (für Normalspannungen aus Normalkraft und Biegemomenten)
- Statische Momente (für Schubspannungen aus Querkräften)
- Dicke (für Schubspannungen aus Querkräften und Torsionsmoment)
- Kernfläche bei geschlossenen Querschnitten (für Schubspannungen aus Torsionsmoment)
Schubspannungen
Bei dünnwandigen Querschnitten kann vereinfacht angenommen werden, dass die Schubspannung parallel zur Wand des Querschnitts verläuft. Daher werden die Anteile der Schubspannungen addiert, die sich aus den beiden Komponenten der Querkräfte ergeben. Das Vorzeichen des statischen Moments legt dabei fest, welche Anteile positiv oder negativ angesetzt werden.
Die Schubspannung infolge des Torsionsmoments ist für die Gesamtschubspannung unterschiedlich zu betrachten – je nachdem, ob ein offener oder ein geschlossener Querschnitt vorliegt. Bei einem offenen Querschnitt wird die Torsionsschubspannung derjenigen Summe aus den einzelnen Schubspannungen mit dem Vorzeichen zugerechnet, die zum größeren Absolutwert der Summe führt. Bei einem geschlossenen Querschnitt hingegen wird die Torsionsschubspannung einfach zur Summe aus den einzelnen Schubspannungen addiert. Dabei werden die Vorzeichen bei Kernfläche und statischen Momenten so eingestellt, dass sie mit der programminternen Vorzeichenkonvention der Schubspannung übereinstimmen, die von der Belastung abhängt.
Doppelte Spannungspunkte
Spannungspunkte, die innerhalb des Querschnitts liegen, lassen die oben erwähnte Annahme nicht zu, dass die Schubspannung parallel zur Wand des Querschnitts verläuft. Hier kommt ein spezielles Verfahren mit doppelten Spannungspunkten zur Anwendung, bei dem zwei Spannungspunkte mit identischen Koordinaten im Querschnitt erzeugt werden. Der eine Spannungspunkt erfasst das statische Moment um die Achse y (Parameter für Schubspannung infolge vertikaler Querkraft), der andere das statische Moment um die Achse z (Parameter für Schubspannung infolge horizontaler Querkraft). Bei diesen Spannungspunkten ist das komplementäre statische Moment jeweils null.
Den Doppelspannungspunkten können unterschiedliche Dicken zugeordnet sein, die sich ebenfalls auf die Berechnung der Schubspannung auswirken. Die Schubspannungen werden als zueinander senkrecht wirkende Komponenten betrachtet, die voneinander abhängig sind – es sind zwei Komponenten eines Spannungszustands. Für die Ermittlung der Gesamtschubspannung werden beide Anteile quadratisch addiert. Die Schubspannung infolge des Torsionsmoments wird in diesen Punkten nicht betrachtet.
Die Schubspannungen von Ergebniskombinationen, die in den Doppelspannungspunkten vorliegen, dürfen nicht linear kombiniert werden. Daher werden die Extremwerte beider Komponenten mit den zugehörigen komplementären Schubspannungen ausgewertet, um daraus die größte Gesamtschubspannung zu bestimmen.