Eingabe des Schalenmodells
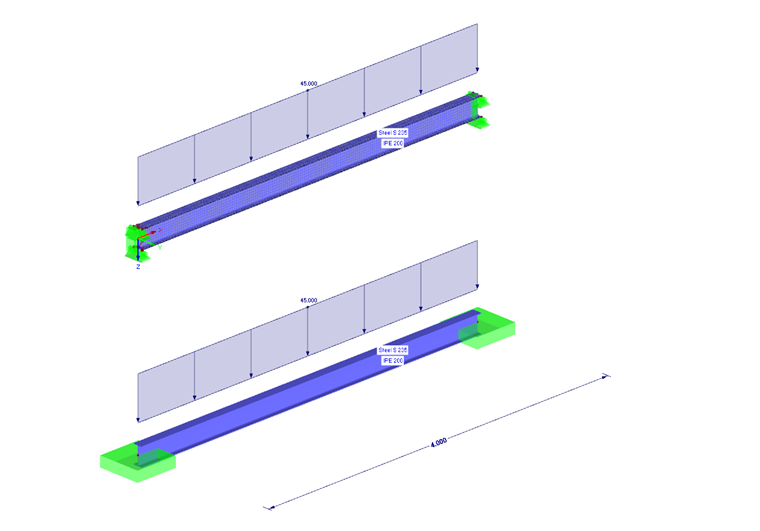
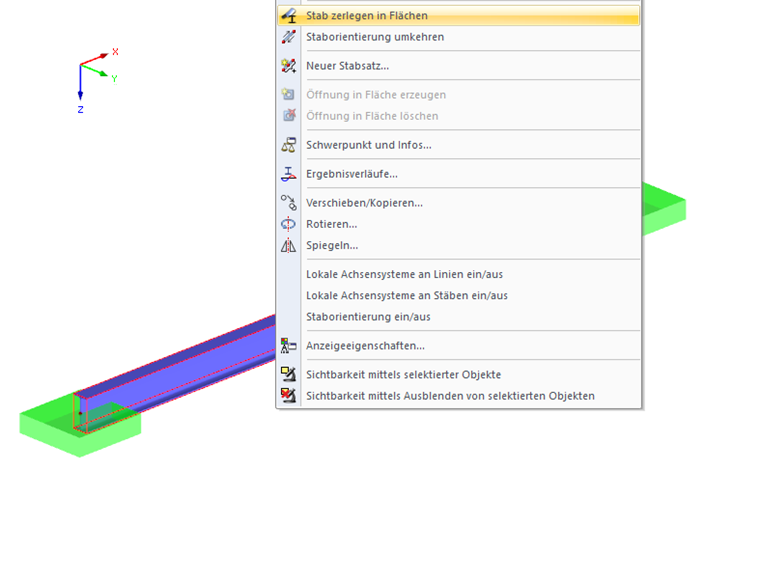
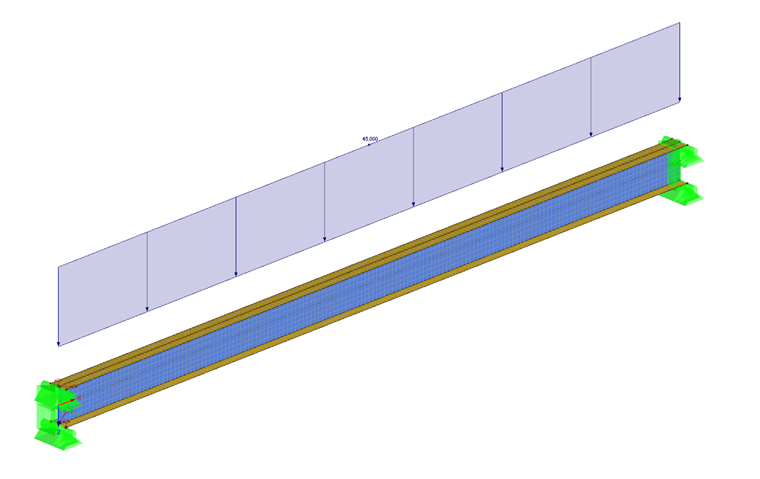
Die Erstellung des Schalenmodells kann man in RFEM sehr einfach durchführen. Hier hat man die Möglichkeit, ein Stabmodell direkt in Flächen zu zerlegen (Funktion "Stab zerlegen in Flächen"). Zuerst erstellt man einen Stab mit der Länge 4 m. Als Querschnittstyp wird ein IPE 200 gewählt. Nach der Eingabe des Trägers zerlegt man diesen in Flächen mittels oben genannter Funktion.
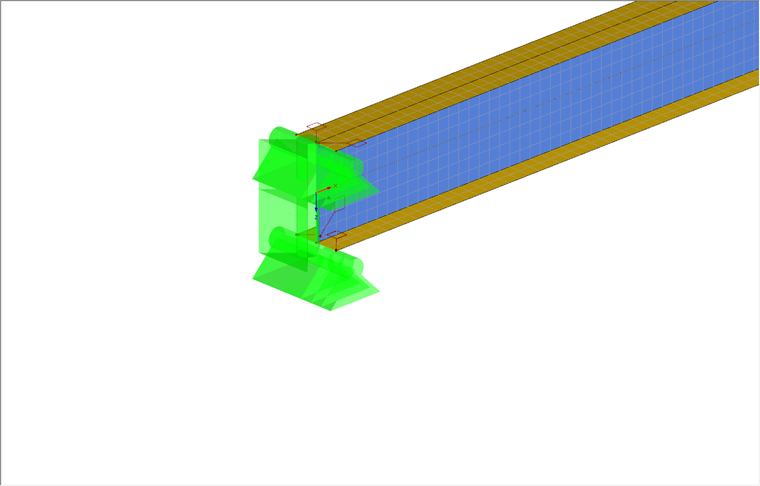
Nachdem man nun ein reines Schalenmodell des Trägers erstellt hat, werden die Randbedingungen definiert. Hier soll es sich um einen beidseitig eingespannten Träger handeln. Diese Randbedingungen kann man mit Hilfe von Linienlagern erstellen. Dabei lagert man den Steg und die beiden Flansche des Flächenmodells mit Hilfe von Linienlagern. Eine komplette Einspannung der Lager ist dabei nicht nötig, da sich die Einspannung aus der Begrenzung der Wegfreiheitsgrade an Steg und Flansch ergibt.
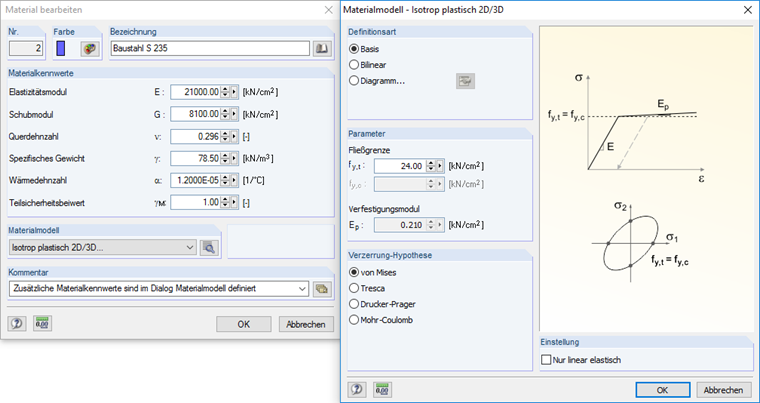
Nach der Eingabe der Randbedingungen gibt man den Flächen die plastische Eigenschaft, indem man das Materialmodell für die Flächen zu einem plastischen 2D/3D-Material ändert. Bei diesem Materialmodell ist man in der Lage, eine Plastifizierung der Flächen während der Berechnung zu berücksichtigen. Dabei wird hier die Vergleichsspannung nach von Mises als Streckgrenze des Materials mit 24 kN/cm² vorgegeben. Stellt man das Material auf ein plastisches Verhalten um, so wird automatisch in den Berechnungsparametern die Laststeigerung aktiviert. Die Laststeigerung führt bei der Berechnung zu einem besseren Konvergenzverhalten.
Die Belastung der Struktur ist hier eine Linienlast, welche an der Schnittlinie zwischen oberem Flansch und Steg erstellt wird. Die Belastung wird mit 45 kN/m angenommen, da sich bei dieser Last bereits plastische Gelenke in beiden Auflagerbereichen ausbilden.
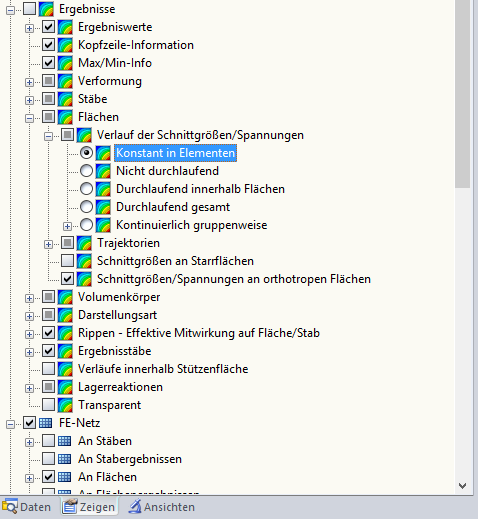
Nach der Berechnung der Gesamtstruktur erhält man zuerst die Verformungen. Hier hat man nun die Möglichkeit auf die von-Mises-Vergleichsspannung zu schalten. In der Standardeinstellung von RFEM werden die Spannungen geglättet angezeigt. Dies führt zu einer verzerrten Ergebnisdarstellung, da die plastische Maximalspannung überschritten ist. Daher ist es notwendig, die Schnittgrößen und Spannungen, welche in der Fläche angezeigt werden, auf "Konstant in Elementen"umzustellen. Diese Form der Ergebnisausgabe bildet den Mittelwert über jedes FE-Element. Dazu werden die Knotenwerte eines FE-Elements zur Mittelwertbildung verwendet. Bei der Verwendung eines plastischen oder nichtlinearen Materialverhaltens ist immer die Darstellung "Konstant in Elementen" zu wählen, da das Materialverhalten die Elementwerte plastifizieren lässt und somit auch die plastische Spannung im Nachgang korrekt angezeigt wird.
Um nun einen Vergleich mit der analytischen Berechnung zu führen, ist es nötig, die Ergebnisse des Flächenmodells vergleichbar mit denen des analytischen Modells zu machen. Hier gibt es nun die Möglichkeit einen Ergebnisstab zu verwenden. Mit Hilfe dieses Stabes ist es im Programm möglich, Flächenspannungen oder Volumenspannungen in Stabschnittgrößen aufzuintegrieren. Damit kann man im Anschluss den Vergleich zum analytischen Modell ziehen.
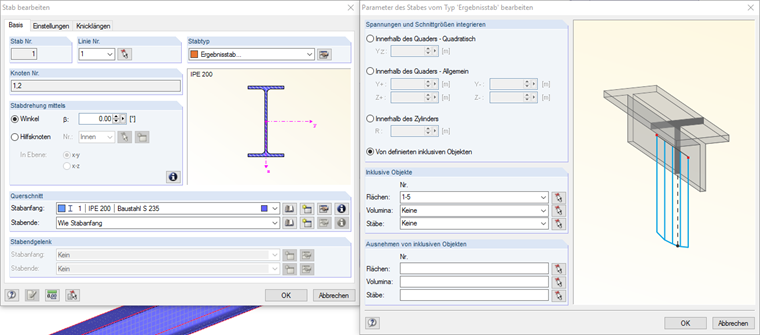
Die Definition des Stabes ist in diesem Modell sehr einfach zu realisieren. Löst man einen Stab in ein Flächenmodell auf, so entsteht an der Stelle des ursprünglichen Stabes ein sogenannter Nullstab, quasi als Platzhalter. Dieser Stab besitzt keine Steifigkeit und wird in der Berechnung auch nicht berücksichtigt. Hier ändert man nun den Stabtyp von Nullstab auf Ergebnisstab und weist über die Eigenschaften diesem neuen Ergebnisstab alle Flächen zu, welche zur Berechnung der internen Schnittgrößen mitverwendet werden sollen. In diesem Beispiel nimmt man dazu einfach alle Flächen des Schalenmodells, da hier die Spannungen aus Flansch und Steg in Stabschnittgrößen aufintegriert werden sollen.
Eingabe des Stabmodells
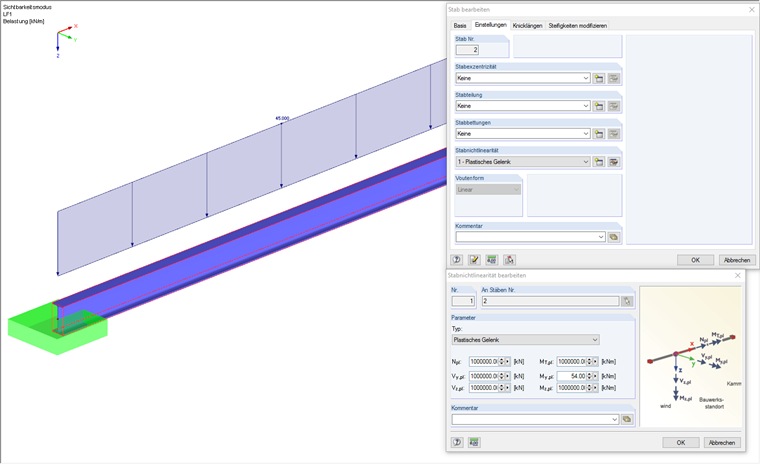
Als Vergleich wird nun ein einfaches Stabmodell erstellt, welches ein plastisches Gelenk ausbilden soll. Daher erstellt man einen einfachen Stab mit dem QuerschnittIPE 200. Für diesen Stab wird im Anschluss ein weiteres Material angelegt, welches über isotrope Materialeigenschaften verfügt. Hier wird ein Stahl der Güte S235 gewählt. Im Anschluss hat man unter den Stabeigenschaften die Möglichkeit ein plastisches Gelenk zu berücksichtigen. Da sich in diesem Beispiel nur ein plastisches Momentengelenk ausbilden soll, werden alle übrigen Schnittgrößen mit einem sehr großen Wert angenommen, damit diese nicht wirken. Das plastische Grenzmoment für einen IPE 200 mit S235 beträgt:
Mply = fy ∙ Wply
Mply = 24 kN/cm2 ∙ 220,6 cm3 = 54 kNm
Die Randbedingungen werden als beidseitig eingespannt angenommen, um mit dem Flächenmodell vergleichbar zu bleiben. Die Belastung wird in diesem Beispiel als Stablast aufgebracht, da Linienlasten nur für Flächen zu verwenden sind. Die maximale Stablast beträgt hier 45kN/m.
Auswertung der Vergleichsberechnung
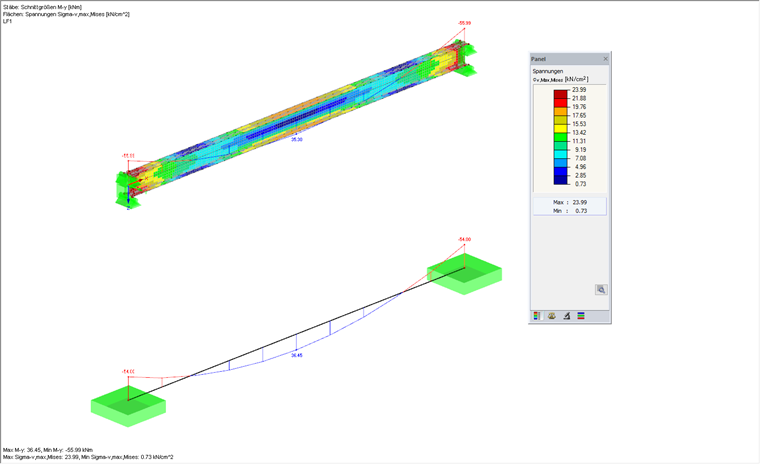
Das Ergebnis beider Berechnungen wird nun in nachfolgender Grafik verglichen. Es zeigen sich dabei fast identische Resultate. Man kann am Flächenmodell deutlich sehen, dass sich plastische Gelenke im Auflagerbereich ausbilden. Die daraus resultierenden Schnittgrößen im Ergebnisstab sind daher sehr ähnlich zu den Schnittgrößen des Stabmodells, welches über eine plastische Gelenkausbildung verfügt. Die Unterschiede sind auf die Modellierung des Flächenmodells und die Idealisierung des Stabmodells zurückzuführen.
.png?mw=350&hash=b023d6c658e181cb7d69028c0f3994dedab96fc5)
.jpg?mw=350&hash=bd355674e865e37d5548c329b8f5f0153cefe276)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)