1D 单元(一维单元)
对于杆件单元,程序默认假定梁符合平截面假定(RFEM默认梁为Timoshenko梁)。 “一维单元”用于计算杆件(梁、桁架、肋、索和刚性杆等)。 一维杆件单元共有 12 个自由度,单元始端 6 个,末端 6 个自由度,分别对应位移(ux 、uy 、uz )和转角(φx 、φy 、φz ). 结构进行线弹性计算时,程序使用三次多项式模拟杆件的轴力、扭矩沿杆身的变化情况,位移和转角独立插值。 程序会默认考虑荷载和荷载的影响。 刚度矩阵KL (12, 12)描述了一维单元的线性行为。 矩阵KNL (12, 12) 描述了几何非线性问题中的轴力和弯矩之间的相互作用。 关于更多介绍可以参阅参考文献[1] 和[2]。
当程序进行三阶大变形分析时,建议对线进行线网格细化来保证计算结果的准确性。
2D 单元(二维单元)
程序将模型中的面离散为二维单元。 二维单元分为四边形单元和三角形单元,程序划分网格时优先使用四边形单元,在无法使用四边形单元的位置使用三角形单元划分。
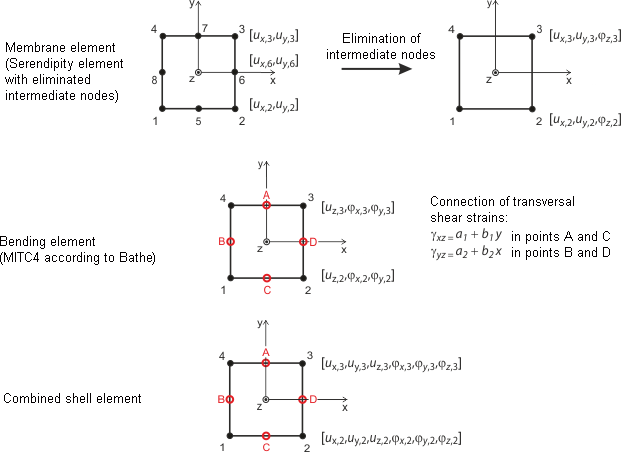
与一维单元的结点相同,四边形单元和三角形单元的角部结点也拥有6个自由度: 位移(ux ,uy ,uz )和转角(φx ,φy ,φz )。 以保证一维单元和二维单元相互耦合。 二维单元的自由度参照局部坐标系进行描述,组装全局刚度矩阵时通过位置转换将元素添加到全局刚度矩阵对应的位置。
图片 {% 许多#image025629 壳的四边形单元 ]] 显示的是平面壳单元。它是基于 Mindlin/Reissner 理论的。为确保与杆件单元直接耦合,请在壳平面 (ux, uy ) 上选择平方。通过消除中间节点,创建一个四节点单元,在 x、y 和 z 方向上都有额外的转动自由度。以使二维平面单元可以与一维单元直接耦合。 Bathe 和 Dvorkin 的方法 {% 许多分#Refer [3]]] presented 已经使用 MITC 单元(张量分量的混合插值): 其中,MITC3+适用于三角形平面单元,MITC4适用于四边形平面单元。
程序中的杆件单元默认为Timoshenko梁, 默认不考虑翘曲效应。
Mindlin板可以视为Timoshenko梁在二维情况下的推广 [4] [5] [6] 。 例如对三角形平面单元,其基本函数被划分为三个位移函数、三个应变函数和三个插值函数。 MITC元的应变场为线性场,变形场可用二次函数描述。 单元刚度矩阵KL被转换成 ux, uy, φz类型的 9 个刚度矩阵。 相互叠加得到总刚度矩阵 。 该矩阵是 Lynn/Dhillon 概念的结果。 Timoshenko梁的位移和转角各自独立插值, Mindlin板(具有明显剪切变形的板)也使用了相同的原理。 通过这种方式,RFEM 可以精确计算厚板和薄板(Kirchhoff板)。
在考虑几何非线性问题时,应力-应变条件无法分解为平面状态和弯曲/剪切状态。 矩阵KNL考虑了这些状态的相互影响。 RFEM 基于 Zienkiewicz 的方法,在程序中使用了一种相当简单但有效的矩阵NL K 的矩阵 [7] 。 应用格林/拉格朗日应变张量 ε = ε1+ ε 2的平方分量。 平面应力条件下的线性分布 uz(x, y)以及与弯曲相互作用的线性分布 ux(x, y) 和 uy(x, y) 这种假设是可能的,因为主要的相互作用影响取决于微分方程的一阶求导,高阶分量的影响会随着分解成更小的单元而迅速减少。 这种方法的正确性已经通过大量的数值分析得到证明。
3D 单元(三维单元)
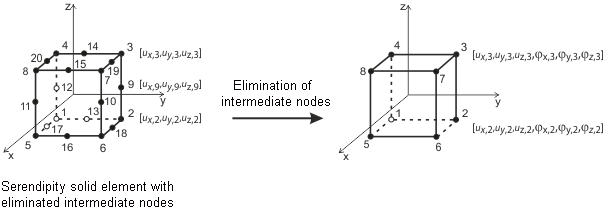
程序会将实体对象离散为3D 单元 。 RFEM中的三维单元类型有: 四面体、五面体和六面体。 不同类型的三维单元的应用范围和刚度矩阵, 可以参阅参考文献 [8]。 用户可以向 Dlubal Software 索取该文档。
在三维单元中,旋转自由度非常关键。 因为三维单元的变形完全取决于结点的位移,三维单元的刚体旋转(例如奇异扭转)不会影响三维单元内部的变形。