Конечные элементы в RFEM

Элементы 1D

Для стержневых элементов предполагается, что сечение при деформации остается плоским. «1D элементы» используются для представления балок, ферм, ребер, вантов и жестких соединений. Одномерный элемент стержня имеет в общей сложности двенадцать степеней свободы - шесть в начале и шесть в конце элемента, каждая для перемещения (_ux, u_y, u_z ) и поворотов (φ_x, φ_y, φ_z ). При линейном расчете данных, растяжение, сжатие и кручение выражаются в виде линейных функций оси стержня x, независимо от изгиба и сдвига. Эти функции аппроксимируются полиномом третьего порядка по x, с учетом влияния касательных напряжений от поперечных сил V_y и V_z. Матрица жесткости K_L (12, 12) описывает линейное поведение одномерных элементов. В случае геометрически нелинейных задач, взаимодействие между осевой силой и изгибом, выражается в матрице жесткости K_NL (12, 12). Для получения дополнительной информации, смотри {%><#RБыло применено [3]]] представленных элементов MITC ( ''смешанная интерполяция тензорных компонентов'' ): MITC3+ для треугольников, MITC4 для четырехугольников. В настоящее время элементы стержней учитываются путем прямого решения дифференциального уравнения по методу второго порядка. Эффекты депланации не могут учитываться при использовании кручения по Сен-Венану. Расчеты мембраны основаны на принципах Бергана {%><#Refer [4]]] {%><#Refer [5]]] {%><#Refer [6]]]. Например, для треугольных элементов основные функции разделены на три деформации жесткого тела, три постоянных условия деформации и три специальных линейных градиента напряжения и деформации. Поле деформации в элементе является квадратичным и поле напряжений является линейным. Матрица жесткости элемента '''K_L''' затем преобразуется в девять общих параметров типа u_x, u_y, φ_z. Компоненты данной матрицы вставляются вместе с компонентами для изгиба и сдвига в общую матрицу жёсткости (18, 18). Данная матрица является результатом применения концепции Линна/Дхиллона. Таким образом, применяются и рассчитываются по Тимошенко так называемые плиты Миндлина (плиты с отчетливой деформацией сдвига). Таким образом, RFEM находит правильное решение как для толстых, так и для тонких пластин (плиты Навье). В случае геометрически нелинейных задач, вышеупомянутое разделение напряженно-деформированного состояния на плоское состояние и при изгибе/сдвиге невозможно. Взаимное влияние этих состояний учитывается в матрице '''K_NL'''. RFEM использует довольно простую, но эффективную форму матрицы K_NL, которая основана на подходах Ценкевича [[Refer [7]]]. При этом применяется квадратная составляющая ε₂ тензора деформаций Грина/Лагранжа ε = ε₁ + ε₂. Предполагается линейное распределение u_z (x, y) для плоского напряженного состояния и линейное распределение u_x (x, y) и u_y (x, y) для взаимодействия с изгибом. Это предположение возможно, потому что основной эффект взаимодействия зависит от первого вывода дифференциального уравнения, и потому влияние компонентов более высокого порядка быстро уменьшается с делением на более мелкие элементы. Правильность данного метода была подтверждена несколькими численными расчетами.

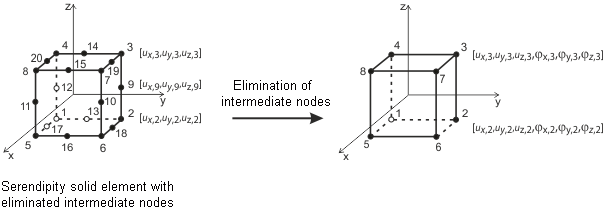
== Элементы 3D == '''3D элементы''' используются для тел. В программе RFEM реализованы следующие типы элементов: четырехгранник, пятигранник (призма, пирамида) и шестигранник. Для получения подробной информации о примененных элементах и матрицах подробности см. в статье Севцика' ''о трехмерных конечных элементах с поворотными степенями свободы'' {%ref#Refer [8]]]. Данную документацию можно легко запросить в компании Dlubal Software. Как правило, для тел все степени свободы вращения должны рассматриваться как критические. Поскольку деформация тела определяется исключительно из векторов перемещения, поворот узла сетки (например, из-за сингулярного кручения) не влияет на деформацию тела.