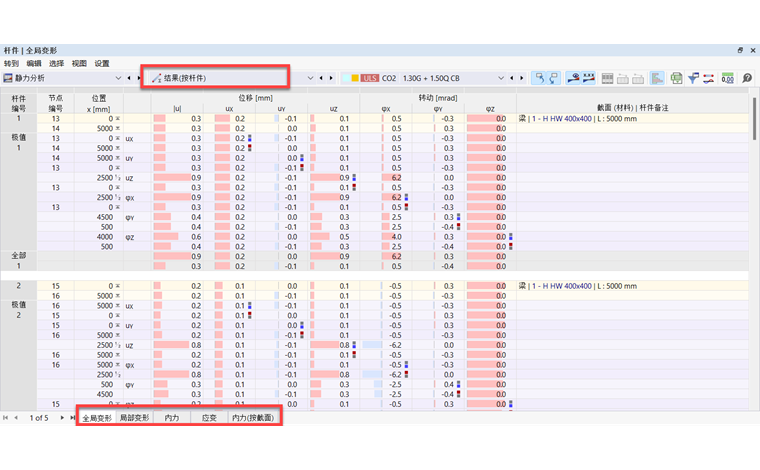
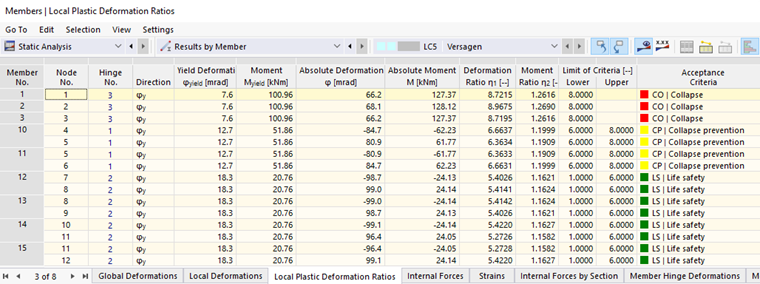
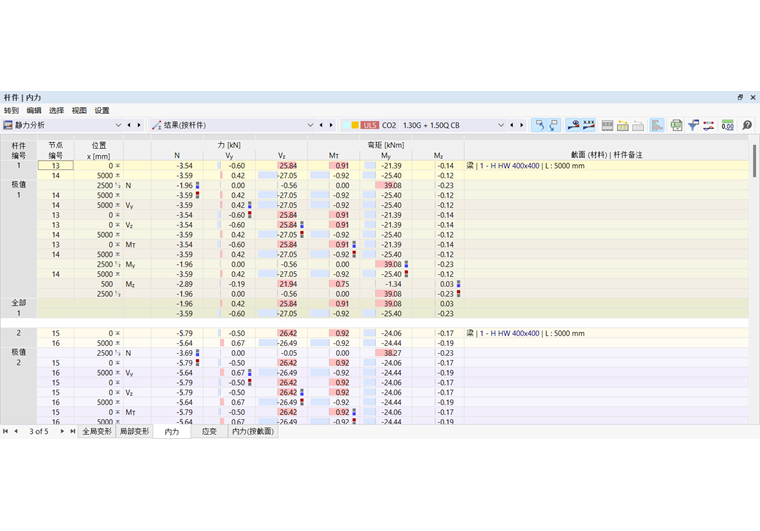
您可以通过导航器类别杆件图形化显示杆件的结果。数值杆件结果可以在表格类别按杆件结果中找到。
变形
图像显示了全球杆件形变的表格。这些是相对于X,Y和Z轴的。局部变形是相对于杆件的轴,这些轴的名称取决于基本设置中的规定(见章节 设置和选项 )。
局部杆件轴系统也影响变形的符号:正位移方向为正局部轴的方向,正旋转为绕正杆件轴的顺时针方向。
对于不对称截面,您可以在导航器中设置结果是相对于主轴u和v还是标准输入轴y和z(见图)。
局部位移和旋转的含义为:
| |u| | 总位移的绝对值 |
| ux | 沿局部x轴的位移 |
| uy | 沿局部y轴的位移 |
| uz | 沿局部z轴的位移 |
| φx | 绕局部x轴的旋转 |
| φy | 绕局部y轴的旋转 |
| φz | 绕局部z轴的旋转 |
表格列出了每个杆件在 结果表格管理器 中定义的点的变形。在那里您还可以控制哪些极值将被输出。
如果您定义了一个具有塑性属性的 杆端接头 ,表格'局部塑性变形的利用率'中将输出屈服应力,屈服内力和接受标准。
内力
在导航器中设置哪些内力将在杆件上显示。对于不对称截面,您也可以选择结果是相对于主轴u和v还是标准输入轴y和z(见图)。这也会影响表格中的输出。
图形内力曲线基于有限元网格节点中的结果值。根据对话框 网格设置 中的设置生成。
表格列出了每个杆件在 结果表格管理器 中定义的点的内力。在那里您还可以控制哪些极值将被输出。
杆件内力的意义为:
| N | 沿杆件纵向x轴的轴力 |
| Vy | 沿局部y轴的剪力 |
| Vz | 沿局部z轴的剪力 |
| MT | 绕杆件纵向x轴的扭矩 |
| My | 绕局部y轴的弯矩 |
| Mz | 绕局部z轴的弯矩 |
| v | 横向剪力(板与杆之间的纵向剪力) |
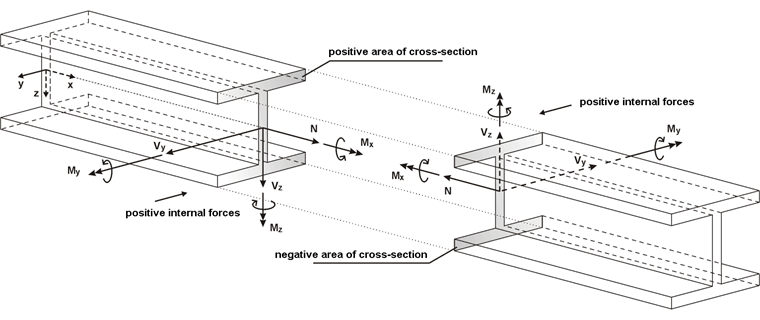
局部杆件轴系统影响内力的符号。
弯矩My为正时,在杆件的正侧(沿z轴的方向)产生拉应力。Mz为正时,在杆件的正侧(沿y轴方向)产生压应力。扭矩,轴力和剪力的符号定义符合常规惯例:这些内力在正截面上以正方向作用时为正。
上述的内力规则仅适用于局部杆件轴z向“下”定义的情况(见章节 设置和选项 )。如果局部z轴是“上”定义的,则正弯矩My在杆件正侧会产生压应力,正弯矩Mz产生拉应力。
类别‘按杆件结果’的其他表格中,杆件内力根据特定标准汇总。您可以在表格‘按截面内力’中查看每个截面的极值。
应变
杆件应变表示局部变形,以拉伸和剪切的形式表现。根据胡克定律,由杆件应力得出。
空间应变状态的应变张量在章节 体积模型 中描述。对一维杆件元素,矩阵简化为:
剪切根据以下方程确定:
杆件应变的意义为:
| εx | 沿杆件轴x的拉伸 |
| γxy | 沿杆件轴y的剪切 |
| γxz | 沿杆件轴z的剪切 |
| κx | 绕杆件轴x的弯曲 |
| κy | 绕杆件轴y的弯曲 |
| κz | 绕杆件轴z的弯曲 |
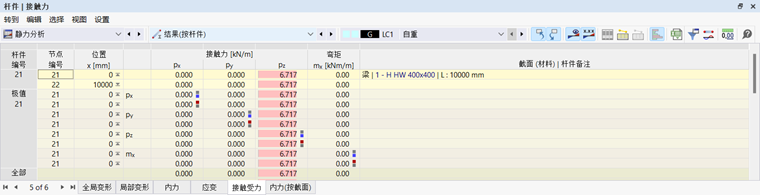
接触力
接触力px, py和pz沿各自的杆件轴方向起作用。它们以单位长度输出。对于不对称截面,您可以在导航器中设置结果是相对于主轴u和v还是标准输入轴y和z(见图)。
绕杆件纵向轴的接触矩mx也以单位长度输出。
载荷和支座力的总和
在荷载情况下和荷载组合中,载荷和支座力的校验总和Σ将在表格末尾给出。如果模型还存在节点、线或表面支座,这个平衡将显示差异。这些支座力在总平衡中也应考虑。
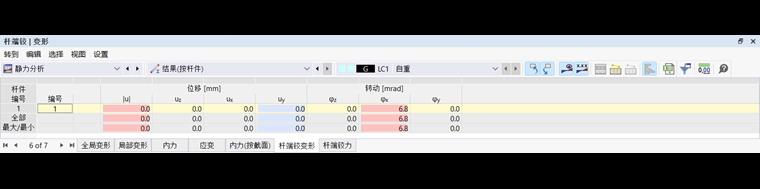
杆端铰接变形
对于有的杆件,您可以在表格中显示‘杆端铰接变形’。它说明了每个铰链传递了哪些位移或旋转。
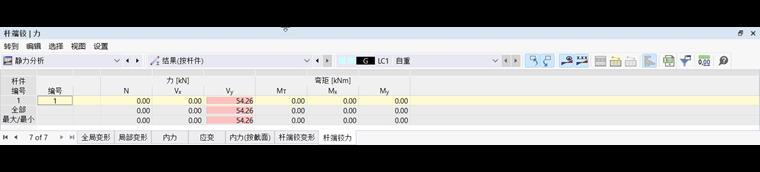
杆端铰接力
对于有的杆件,您可以在表格中显示‘杆端铰接力’。它说明了每个铰链传递了哪些力或力矩。
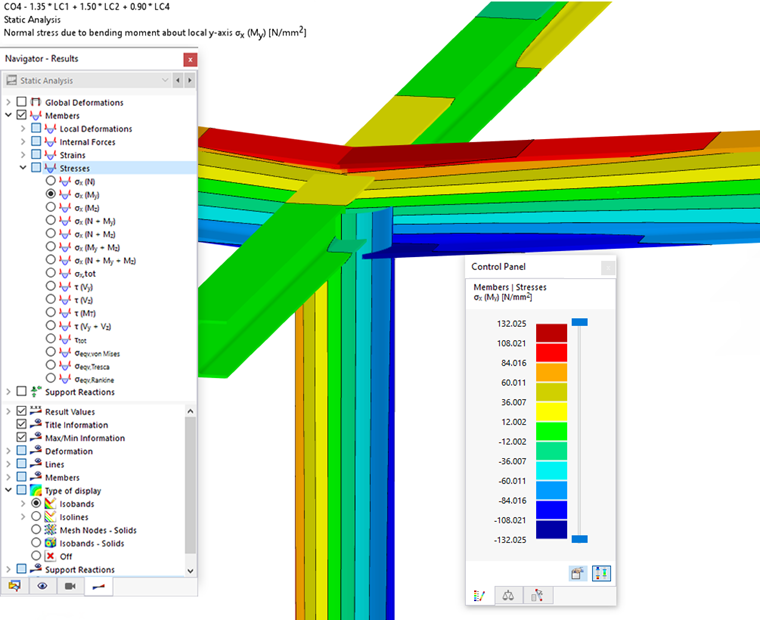
应力
‘应力’类别的条目使得可以图形化地显示杆件截面的普通应力、剪应力和比较应力的分布。这不需要https://www.dlubal.com/de/produkte/add-ons-fuer-rfem-6-und-rstab-9/bemessung/spannungs-dehnungs-berechnung应力-应变计算的附加功能的许可。然而,对结果组合和设计情况下的包络结果,没有截面应力的输出可能。
‘应力’类别提供了多种应力组分和组合选项。例如,您可以查看因弯曲而产生的拉应力和压应力的分布,这些应力在I型截面的翼缘上出现。值的分配在面板中是规则化的。在章节中描述了如何调整颜色和值。
应力通过有限元计算从内力和截面特性获得。