Elementos finitos en RFEM

Elementos en 1D

Para elementos de barra, se asume que la sección permanece plana cuando se deforma. Los 'Elementos en 1D' se utilizan para representar vigas, cerchas, nervios, cables y acoplamientos rígidos. Un elemento de barra 1D tiene un total de doce grados de libertad − seis al inicio y seis al final del elemento, cada uno para los desplazamientos (_ux, u_y, u_z ) y giros (φ_x, φ_y, φ_z ). Al calcular los datos estructurales linealmente, la tracción, compresión y torsión se expresan como funciones lineales del eje x de la barra, independientemente de la flexión y el cortante. Estas funciones se aproximan mediante un polinomio de tercer orden en x, incluyendo la influencia de las tensiones tangenciales de los esfuerzos cortantes V_y y V_z. La matriz de rigidez K_L (12, 12) describe el comportamiento lineal de los elementos 1D. La interacción mutua entre el esfuerzo axil y la flexión en el caso de problemas geométricamente no lineales se expresa en la matriz de rigidez _KNL (12, 12). Para obtener más información, consulte [1] y [2].

Para cálculos según el análisis de grandes deformaciones, se recomienda utilizar un Refinamiento de malla de líneas para que los resultados de la barra se puedan determinar con la precisión correspondiente.

Elementos en 2D

Para las superficies, se crean Elementos en 2D. Donde no se pueden usar elementos cuadrangulares, el generador de malla inserta elementos triangulares.

Los grados de libertad de los elementos cuadrangulares y triangulares en los nudos de esquina son los mismos que para los elementos en 1D: grados de libertad del desplazamiento (u_x, u_y, u_z) y giro (φ_x, φ_y, φ_z). Esto asegura la compatibilidad entre los elementos en 1D y 2D en los nudos. Los parámetros se definen en el sistema de coordenadas local plano de los elementos y se convierten en el sistema de coordenadas global al componer la matriz de rigidez global.

Elementos cuadrangulares para láminas en RFEM

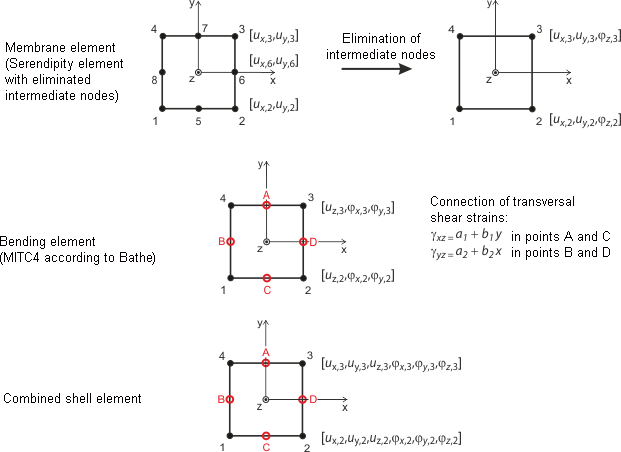
La imagen Elementos cuadrangulares para láminas muestra la aproximación para elementos planos de láminas. Se basa en la teoría de Mindlin/Reissner. Para asegurar el acoplamiento directo con los elementos de la barra, se elige una aproximación cuadrada en el plano de la lámina (_ux, u_y ). Al eliminar los nudos intermedios, se crea un elemento de cuatro nudos con grados de libertad de giro adicionales en las direcciones x, y y z. Por lo tanto, es posible un acoplamiento directo con elementos de viga para elementos de diafragma. Basado en una interpolación combinada de desplazamientos transversales, giros de la sección y deformaciones por cortante transversal, los métodos de Bathe y Dvorkin [3] presenta los elementos MITC ( interpolación mixta de componentes tensoriales ): MITC3+ para triángulos, MITC4 para cuadrángulos.

En la actualidad, se consideran los elementos de barra al resolver directamente la ecuación diferencial según el análisis de segundo orden. Los efectos de alabeo no se pueden considerar cuando se usa la torsión de Saint Venant.

Los cálculos de las membranas se basan en los principios de Bergan [4] [5] [6]. Para elementos triangulares, por ejemplo, las funciones básicas se subdividen en tres deformaciones de cuerpo rígido, tres condiciones de deformación constante y tres gradientes lineales especiales de tensión y deformación. El campo de deformación dentro de un elemento es cuadrático y el campo de tensiones es lineal. La matriz de rigidez del elemento K_L se transforma posteriormente en nueve parámetros colectivos de los tipos_ux, u_y, φ_z. Los componentes de esta matriz se insertan junto con los componentes para flexión y cortante en la matriz de rigidez general (18, 18). Esta matriz es el resultado del concepto de Lynn/Dhillon. De esta manera, se aplican las llamadas placas de Mindlin (placas con una deformación por cortante distinta) y se analizan según Timoshenko. De esta manera, RFEM encuentra la solución correcta tanto para placas gruesas como finas (placas según el método de Navier).

En caso de problemas geométricamente no lineales, no es posible dividir la condición tensión-deformación en un estado plano y en flexión/cortante mencionada anteriormente. Las influencias mutuas de estos estados se consideran en la matriz _KNL. RFEM utiliza una forma bastante simple pero eficaz de la matriz KNL que se basa en los enfoques de_Zienkiewicz [7]. Se aplica la componente cuadrada ε₂ del tensor de deformación de Green/Lagrange ε = ε₁ + ε₂. Se suponen una distribución linear de u_z(x, y) de la condición de tensiones planas y distribuciones lineares de u_x(x, y) y u_y(x, y) de la interacción con flexión. Esta suposición es posible debido a que el efecto principal de la interacción depende de la primera derivación de la ecuación diferencial y porque la influencia de componentes de un orden superior disminuye con la división en elementos más pequeños. La exactitud de este procedimiento ha sido probada en varios análisis numéricos.

Elementos en 3D

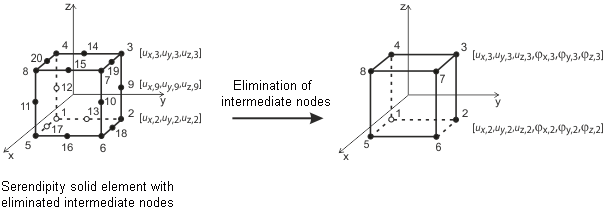
Los Elementos en 3D se utilizan para los sólidos. Los siguientes tipos de elementos están implementados en RFEM: tetraedro, pentaedro (prisma, pirámide) y hexaedro. Para información detallada sobre elementos y matrices aplicados, consulte los 'Elementos finitos en 3D con grados de libertad al giro' de Sevcik [8] para más detalles. Puede solicitarle esta documentación a Dlubal Software.

Elemento sólido (hexaedro)

Generalmente, se deben considerar todos los grados de libertad al giro como críticos para sólidos. Como la deformación de un sólido se determina únicamente a partir de los vectores de desplazamiento, el giro de un nudo de malla (por ejemplo, debido a una torsión introducida de forma singular) no afecta a la deformación dentro del sólido.