1D prvky
Pro prutové prvky se předpokládá zachování rovinnosti průřezu při deformaci prutu. Pro modelování nosníků, příhradových prutů, žeber, lan a tuhých spojení jsou použity 1D prvky. 1D prutový prvek má celkem dvanáct stupňů volnosti - šest na začátku a šest na konci prvku, vždy pro posuny (ux, uy, uz ) a pootočení ( φx, φy, φz ). Tah, tlak a kroucení jsou při lineárním výpočtu vyjádřeny jako lineární funkce souřadnice x prutu nezávisle na ohybu a posouvající síle. Tyto funkce jsou aproximovány polynomem třetího řádu v x, včetně vlivu smykových napětí od smykových sil Vy a Vz. Matice tuhosti KL (12, 12) popisuje lineární chování 1D prvků. Vzájemná interakce mezi normálovou silou a ohybem v případě geometricky nelineárních úloh je vyjádřena v matici tuhosti KNL (12, 12). Další informace naleznete v [1] a [2].
Pokud výpočet probíhá podle teorie III. řádu, doporučujeme pro výsledky prutů odpovídající přesnosti zahuštění sítě prvků linií.
2D prvky
Pro plochy se vytvoří 2D prvky. Tam, kde nelze použít čtyřúhelníkové prvky, vloží generátor sítě trojúhelníkové prvky.
Stupně volnosti čtyřúhelníkových, resp. trojúhelníkových prvků jsou v uzlových bodech stejné jako u 1D prvků: stupně volnosti posunu (ux, uy, uz) a stupně volnosti natočení (φx, φy, φz). Tím je zajištěna kompatibilita mezi 1D a 2D prvky v uzlech. Parametry jsou definovány v rovinném lokálním souřadném systému prvku a při sestavování globální matice tuhosti se přepočítají do globálního souřadného systému.
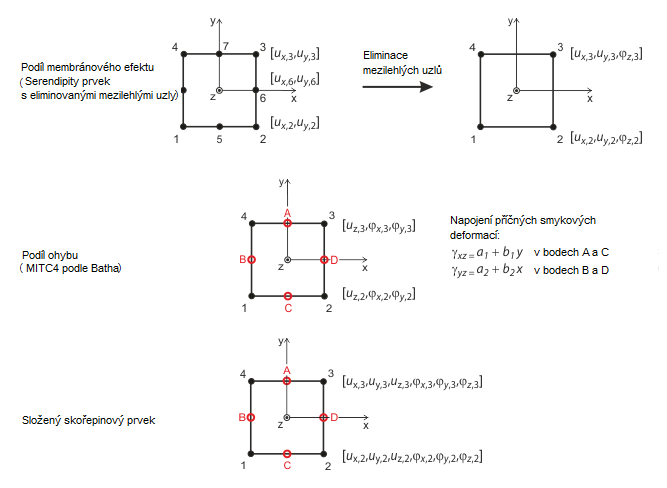
Obrázek Čtyřúhelníkové prvky pro skořepiny ukazuje postup pro rovinné skořepinové prvky. Vychází z Mindlinovy/Reissnerovy teorie. Pro zajištění přímého propojení s prutovými prvky se zvolí kvadratický přístup v rovině skořepiny (ux, uy ). Odstraněním vnitřních uzlů se vytvoří čtyřuzlový prvek s dalšími stupni volnosti natočení ve směru x, y a z. U diafragmových prvků je tak možné přímé spojení s nosníkovými prvky. Metody podle Batheho a Dvorkina založené na kombinované interpolaci příčných posunů, natočení průřezu a příčných smykových přetvořeníRefer [3] prezentované prvky MITC ( Mixed Interpolation of Tensorial Components ) byly použity: MITC3+ pro trojúhelníky, MITC4 pro čtyřúhelníky.
V současnosti se prutové prvky řeší přímo diferenciální rovnicí podle teorie II. řádu. Při postupu Saint-Vénantovou metodou nelze zohlednit kroutící účinky.
Při výpočtu membrány se vychází z Berganova principu [4] [5] [6]. Základní funkce se např. u trojúhelníkových prvků rozloží do třech deformací tuhého tělesa, třech konstantních stavů protažení a třech zvláštních lineárních průběhů napětí/protažení. Deformační pole v prvku je kvadratické a pole napětí lineární. Matice tuhosti prvku KL se následně převede na devět společných parametrů typu ux, uy, φz. Komponenty této matice se spolu s komponenty pro ohyb a smyk vloží do celkové matice tuhosti (18, 18). Tato matice odpovídá Lynn-Dhillonovým předpokladům. Poté se použijí tzv. Mindlinovy desky (desky s nezanedbaným vlivem smykových deformací) a řeší se podle Timošenka. RFEM tak umožňuje řešení jak silných, tak i tenkých (Navierových) desek.
Při geometricky nelineárních úlohách není výše uvedené rozložení vztahu mezi napětím a deformací na rovinné řešení a smyk s ohybem možné. Vzájemné vlivy těchto stavů se zohledňují v matici KNL. RFEM používá poměrně jednoduchý, ale účinný tvar matice KNL, který vychází ze Zienkiewiczových metod [7]. Použije se kvadratická složka ε2 Greenova/Lagrangeova tenzoru deformace ε = ε1 + ε2. Přitom se předpokládá lineární průběh uz(x, y) pro rovinné napětí a lineární průběhy ux(x, y) a uy(x, y) při střídavém působení ohybu. Tento předpoklad lze použít, neboť účinek hlavní interakce závisí na 1. derivaci diferenciální rovnice a vliv členů vyššího řádu velmi rychle klesá při použití menších prvků. Správnost tohoto řešení byla dokázána numerickými testy.
3D prvky
Pro tělesa se používají 3D prvky. V programu RFEM jsou implementovány následující typy prvků: čtyřstěn, pětistěn (hranol, jehlan) a šestistěn. Podrobný popis těchto prvků přesahuje rámec tohoto manuálu. Přesnější informace naleznete v Sevcik: 3D konečné prvky s rotačními stupni volnosti [8]. Tuto dokumentaci si můžete vyžádat u společnosti Dlubal Software.
Obecně je nutné u těles považovat všechny rotační stupně volnosti za kritické. Protože se deformace tělesa stanovuje výlučně z vektorů posunu, pootočení uzlu sítě prvků (např. z důvodu singulárně aplikovaného kroucení) nemá vliv na deformaci v tělese.