Elementos 1D
Para os elementos de barra é assumido que a secção permanece plana quando deforma. Os "elementos 1D" são utilizados para representar vigas, treliças, nervuras, cabos e acoplamentos rígidos. Um elemento de barra tem um total de doze graus de liberdade - seis no início e seis no final do elemento, cada um para os deslocamentos (ux, uy, uz ) e rotações (φx, φy, φz ). ) Quando calcula os dados estruturais linearmente, a tracção, compressão e torção são expressas como funções lineares do eixo x da barra, independente da flexão e corte. Essas funções são aproximadas por uma polinómio de terceira ordem em x, incluindo a influência das tensões de corte a partir das forças de corte Vy e Vz. A matriz de rigidez KL (12, 12) descreve o comportamento linear dos elementos 1D. A interacção mútua da força axial com a flexão no caso de problemas geometricamente não lineares é expressa na matriz de rigidez KNL (12, 12). Para mais informação, ver {%>
Para os cálculos de acordo com a análise de grandes deformações, é recomendada a utilização de um {%>
Elementos 2D
Para superfícies, são criados elementos 2D. Nos casos em que não podem ser utilizados elementos quadrangulares, o gerador de malhas insere elementos triangulares.
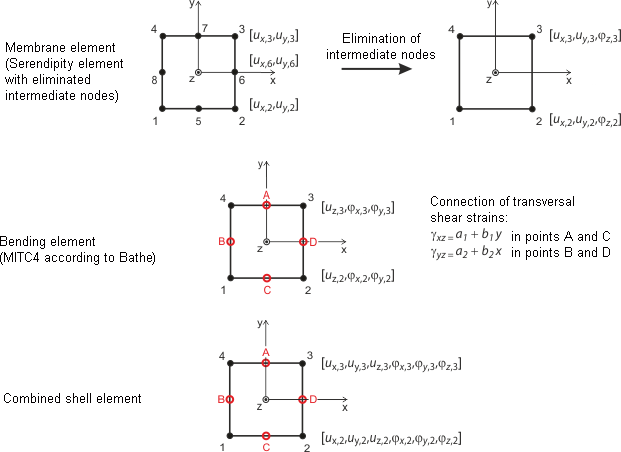
Os graus de liberdade dos elementos quadrangulares e triangulares nos nós de canto são os mesmos como para os elementos 1D: graus de liberdade do deslocamento (ux, uy, uz) e rotação (φx, φy, φz). Isso garante a compatibilidade entre os elementos 1D e 2D nos nós. Os parâmetros são definidos no sistema de coordenadas plano local dos elementos e são convertidos no sistema de coordenadas global quando compõe a matriz de rigidez global.
A imagem {%>#image025629 Elementos quadrangulares para cascas]] mostra a abordagem para elementos de casca planos. Ela é baseada na teoria Mindlin/Reissner. Para assegurar um acoplamento direto com elementos de barra, é escolhida uma abordagem quadrática no plano da casca (ux, uy ). Ao eliminar os nós intermédios, é criado um elemento de quatro nós com graus de liberdade de rotação adicionais nas direções x, y e z. Assim, é possível um acoplamento directo com elementos de viga para elementos de diafragma. Com base numa interpolação combinada de deslocamentos transversais, rotações de secção e extensões de corte transversais, os métodos por Bathe e Dvorkin [3] apresentou elementos MITC ( Interpolação Mista dos Componentes Tensoriais ) foi utilizado: MITC3+ para triângulos, MITC4 para quadrângulos.
Atualmente, os elementos de barra são considerados resolvendo diretamente a equação diferencial de acordo com a análise de segunda ordem. Os efeitos de empenamento não podem ser considerados quando se utiliza a torção de Saint Venant.
Os cálculos de membranas são baseados nos princípios de Bergan {%>KL é então transformado em nove parâmetros colectivos dos tipos ux, uy, φz. Os componentes desta matriz são inseridos em conjunto com os componentes para flexão e corte na matriz de rigidez geral (18, 18). Esta matriz é o resultado do conceito Lynn-Dhillon. Desta forma, são aplicadas as lajes de Mindlin (placas com deformação de corte distinta) e analisadas de acordo com Timoshenko. Desta forma, o RFEM encontra a solução correcta para placas espessas e finas (placas de Navier).
No caso de problemas geometricamente não lineares, a divisão acima mencionada da condição tensão-extensão num estado plano e em flexão/corte não é possível. As influências mútuas desses estados são consideradas na matriz KNL. O RFEM utiliza uma forma bastante simples mas eficaz da matriz KNL que é baseada nas abordagens de Zienkiewicz {%>2 do tensor de tensões de Green/Lagrange ε = ε1 + ε2 é aplicado. Uma distribuição linear de uz(x, y) das condições de tensão planas e das distribuições lineares de ux(x, y) e uy(x, y) é assumida a interacção com a flexão. É possível assumir isto porque o principal efeito da interacção depende da primeira derivação da equação diferencial, e porque a influência dos componentes de uma ordem superior diminuem rapidamente com a divisão em elementos mais pequenos. A exatidão deste procedimento foi provada em diversas análises numéricas.
Elementos 3D
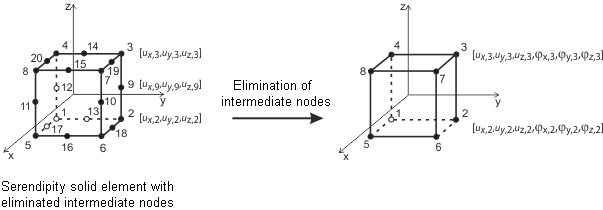
Para os sólidos são utilizados os elementos 3D. Os seguintes tipos de elementos estão implementados no RFEM: tetraedro, pentaedro (prisma, pirâmide) e hexaedro. Para informação mais detalhada sobre elementos aplicados e matrizes, ver Elementos finitos 3D de Sevcik's com graus de liberdade de rotação {%>
Geralmente, todos os graus de liberdade de rotação devem ser considerados críticos para sólidos. Como a deformação de um sólido é apenas determinada a partir dos vectores de deslocamento, a rotação de um nó de malha (por exemplo, devido à particularidade da rotação introduzida) não afecta a deformação no sólido.