返回在线手册

2377x

000483

Dipl.-Ing. （FH）Robert Fogl

2023-04-27

选择手册

概览

图形用户界面和设置

Dlubal 中心

模型 - 基本数据

结构

缺陷

荷载工况和组合

荷载向导

荷载

结构对象

计算

结果

辅助对象

程序功能

结果评估

计算书

按体积结果

您可以通过导航器类别实体体积图形显示体积结果。数值体积结果可以在表格类别逐体积结果中找到。

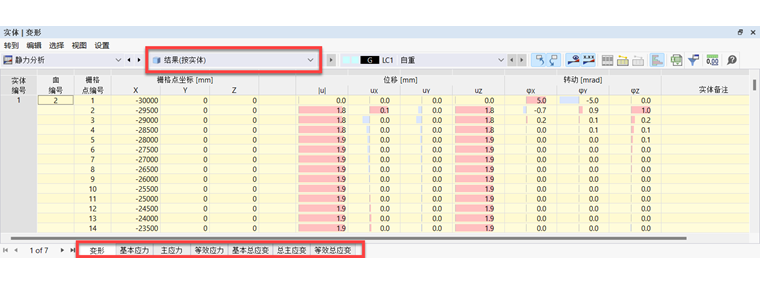
在表格中查看实体的计算结果

信息

在表格和图形中显示体积边界表面的结果。要检查实体内部的结果，请在底部类别表面值中激活选项在有限元网格点。然后可以通过剪切面读取实体内部的值（参见章节剪切面）。

变形

图片逐体积结果旋转表展示了表格中边界表面的变形。位移和旋转在网格点上输出（参见章节网格）。

提示

对于小表面，标准网格间距为0.5米可能导致网格点数很少。在这种情况下，请根据表面大小调整网格点的数量或间距。

变形的含义如下：

\|u\|	总位移的绝对值
u_X	沿全局X轴的位移
u_Y	沿全局Y轴的位移
u_Z	沿全局Z轴的位移
φ_X	围绕全局X轴的扭转
φ_Y	围绕全局Y轴的扭转
φ_Z	围绕全局Z轴的扭转

应力

在导航器中选择实体应力

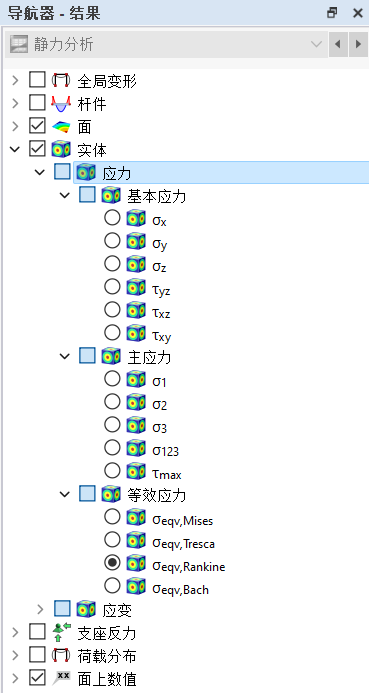
在表格中查看实体的应力

在导航器中指定在实体边界表面显示哪些应力。表格根据在结果表管理器中设定的规则列出这些表面的应力。

体积应力分为以下几类：

基本应力
主要应力
等效应力
应力不变量

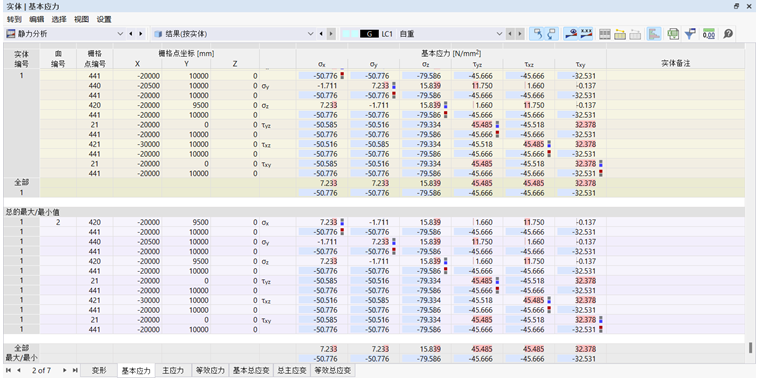
体积应力不像表面应力那样可以用简单的方程式描述。基本应力σ_x、σ_y和σ_z以及剪应力τ_yz、τ_xz和τ_xy由计算核心直接计算。

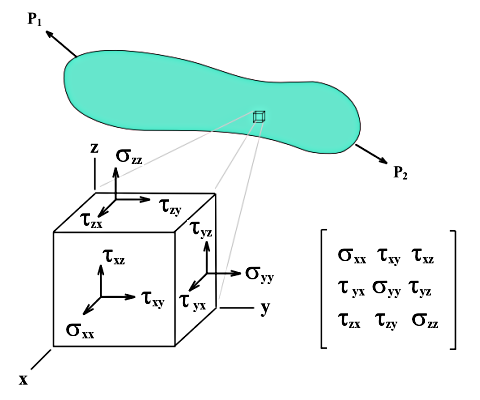
从一个多轴受力的实体中切出一个边长为d_x、d_y和d_z的立方体，可以将立方体表面的应力分解为法向应力和切向应力。在忽略体积力和平行面上的应力差异的情况下，立方体的局部坐标系中的应力状态可由九个应力分量描述。

Volumenelement mit Spannungskomponenten

应力张量的矩阵为：

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

应力张量矩阵

张量的特征值产生了主要应力σ₁、σ₂和σ_{3>如下：

$\det (S - σ E) = 0$

E

3x3 Einheitsmatrix

主应力

最大'''剪应力'''τ_max根据莫尔应力圆确定：

$τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})$

最大剪应力

提示

通过导航器条目'''σ₁₂₃'''可以图形化显示主要应力的轨迹。

'''等效应力'''σ_v根据
冯·米塞斯

的理论，可通过两个等效的公式确定。

$σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}$

由主应力计算的等效应力 σ_v,Mises

$σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}$

根据基本应力计算等效应力 σ_v,Mises

Tresca

等效应力σ_v的计算是通过检查主要应力的差异以确定最大值。

$σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)$

等效应力 σ_v,Tresca

Rankine

等效应力σ_v从主要应力的绝对最大值中得出。

$σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)$

等效应力 σ_v,Rankine

Bach

等效应力σ_v的计算考虑了横向变形率ν，通过研究主要应力差异以找出最大值。

$σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]$

等效应力 σ_{v, Bach}

'''应力不变量'''允许对应力状态进行有针对性的评估。主要应力中求出平均应力p：

$p = \frac{σ_{1} + σ_{2} + σ_{3}}{3} = \frac{I_{1}}{3}$

σ₁ , σ₂ , σ₃

主应力

I₁

第一主应力

平均应力 p

偏差应力q计算如下：

$q = \sqrt{{σ_{1}}^{2} + {σ_{2}}^{2} + {σ_{3}}^{2} - σ_{1} σ_{2} - σ_{2} σ_{3} - σ_{3} σ_{1}}$
$= \frac{1}{\sqrt{2}} \sqrt{{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}} = \sqrt{{I_{1}}^{2} - 3 I_{2}} = \sqrt{3 J_{2}}$

I₁

第一主应力

I₂

第二应力不变量

J₂

第二偏应力不变量

偏差应力 q

洛德角θ可以被视为负载类型的度量。它的范围在-30°和+30°之间，并根据以下公式确定：

$θ = \frac{1}{3} \sin^{- 1} (- \frac{3 \sqrt{3}}{2} \frac{J_{3}}{{J_{2}}^{3 / 2}})$

J₂

第二偏应力不变量: 1/6 [(σ₁ – σ₂)² + (σ₂ – σ₃)² + (σ₃ – σ₂)²]

J₃

第三偏应力不变量: 1/27 (2σ₁ – σ₂ – σ₃) (2σ₂ – σ₃ – σ₁) (2σ₃ – σ₁ – σ₂)

洛德角 θ

== 变形应变 ==}

在导航器中选择体积应变

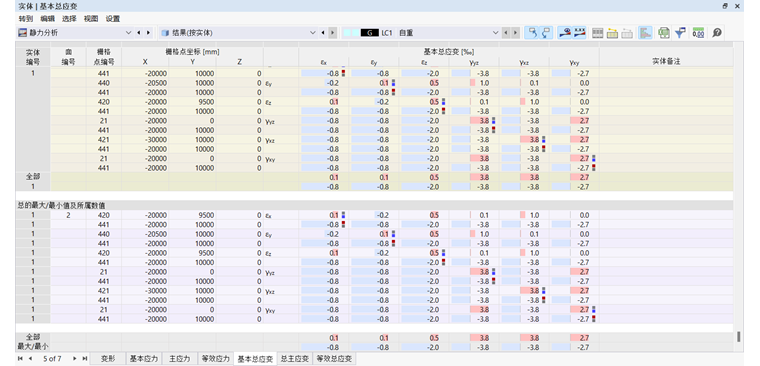
在表格中查看实体的应变

在导航器中指定在实体边界表面显示哪些变形。表格根据在结果表管理器中设定的规则列出这些表面的变形。

体变形应变分为以下几类：

基本总变形
主要总变形
等效总变形
变形不变量

基本总变形以及剪切变形由计算核心直接确定。对于三维变形状态，张量的一般定义为：

ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]

应变状态张量

张量的元素定义如下：

ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})

张量单元

从基本变形中导出主要总变形ε₁、ε₂和ε₃。

提示

通过导航器条目ε₁₂₃可以图形化显示主要变形的轨迹。

等效总变形ε_v根据四个不同的应力假设确定如下。

ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}

等效mises应变 ε_v,Mises

ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)

矩阵（见下文）

等效Tresca应变ε_v,Tresca

ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)

R	Matrix (siehe unten)

等效Rankine应变ε_v,Rankine

ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)

矩阵（见下文）

等效Bach应变 ε_v,Bach

R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]

矩阵 R

变形不变量允许对变形状态进行有针对性的评估。使用主要变形，体积变形不变量ε_v被计算：

ε_{v} = ε_{11} + ε_{22} + ε_{33}

体积变形不变量 ε_v

剪切变形ε_q计算如下：

ε_{q} = \frac{1}{3} \sqrt{2 [{(ε_{11} - ε_{22})}^{2} + {(ε_{22} - ε_{33})}^{2} + {(ε_{33} - ε_{11})}^{2}] + 3 (2 {ε_{12}}^{2} + 2 {ε_{23}}^{2} + 2 {ε_{31}}^{2})}

剪切变形 ε_q

上级章节

结果

I₁	第一主应力
I₂	第二应力不变量
J₂	第二偏应力不变量

J₂	第二偏应力不变量: 1/6 [(σ₁ – σ₂)² + (σ₂ – σ₃)² + (σ₃ – σ₂)²]
J₃	第三偏应力不变量: 1/27 (2σ₁ – σ₂ – σ₃) (2σ₂ – σ₃ – σ₁) (2σ₃ – σ₁ – σ₂)