Der Nachweis einer Bodenplatte aus Stahlfaserbeton besteht aus dem Nachweis der Tragfähigkeit und dem Nachweis der Gebrauchstauglichkeit. Die Vorgehensweise zum Führen des Tragfähigkeitsnachweises wurde bereits in einem vorangegangenen Fachbeitrag erläutert.
Für die dort behandelte Bodenplatte wird nachfolgend der Nachweis der Gebrauchstauglichkeit geführt. Dabei wird gezeigt, wie man mittels iterativ ermittelter FEM-Ergebnisse die entsprechenden Nachweise für den GZG führt.
Eingabe der Topologie und der Lasten
Die Plattengeometrie und Nutzlasten werden von der Bemessung für die Tragfähigkeit übernommen (siehe hierzu den oben genannten Fachbeitrag).
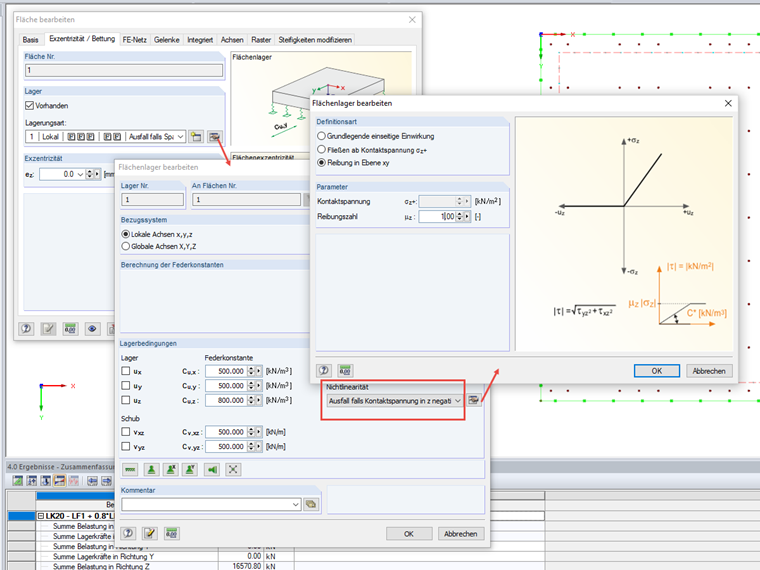
Für die Nachweise der Gebrauchstauglichkeit sind zusätzlich die Zwangseinwirkungen aus Schwinden zu berücksichtigen. Beim Schwinden möchte sich die Bodenplatte zusammenziehen. Durch die Verzahnung beziehungsweise Reibung der Bodenplatte auf dem Untergrund bilden sich Zugspannungen, die berücksichtigt werden müssen. Die Sohlplatte wird auf folgenden Schichtaufbau gebettet (von oben noch unten): Sohlplatte, Folie als Trennlage, Perimeterdämmung, Unterbeton, Baugrund. Gemäß [3], Tabelle 4.19, wird für diesen Schichtaufbau ein Reibungsbeiwert μ0 von 0,8 empfohlen. Für den Bemessungswert μ0,d empfehlen die Autoren von [3] einen Teilsicherheitsbeiwert von γR =1,25.
In RFEM kann der Reibungsbeiwert μ0,d als Nichtlinearität der Flächenbettung definiert werden. Bild 02 zeigt die Einstellmöglichkeit im Programm.
Bei Industriebodenplatten ist für die Ausbildung der Zwangseinwirkung aus Schwinddehnung die vertikale Belastung von großer Bedeutung. Vor dem Einbringen der Regallasten und der Lagergüter ist nur das Eigengewicht der Bodenplatte vorhanden. Dadurch ist der Reibungswiderstand der Bodenplattenunterseite relativ gering. Die aus der Reibung resultierende Zugkraft Nctd (bezogen auf einen 1 m breiten Streifen) in der Sohlplatte bestimmt sich folgendermaßen.
|
Nctd |
Bemessungswert zur Bestimmung der Zugbeanspruchung in der Bodenplatte bei Erreichen der Reibungskraft |
|
μ0,d |
Bemessungswert der Reibung |
|
σ0 |
Sohlspannung |
|
L |
Länge der Sohlplatte für die Verschiebung auf dem Untergrund |
σ0 = 0,19 m ⋅ 1,0 m ⋅ 25 kN/m² = 4,35 kN/m² (Eigengewicht der Platte)
Nctd = 1,0 ⋅ 4,75 kN/m² ⋅ 24,40 m / 2 = 57,95 kN/m
Die aus Reibung maximal resultierende Zugspannung σct,d ergibt sich somit zu
σct,d = Nctd / Act = 57,95 kN/m / 0,19 m = 305 kN/m² = 0,305 MN/m² < ffctm,fl = 2,9 MN/m².
Die aus Reibung resultierende Betonzugspannung unter dem Eigengewicht der Bodenplatte ist kleiner als die Betonzugfestigkeit ffctm,fl. Dadurch kann sich die Schwinddehnung unter der Platteneigenlast rissfrei einstellen.
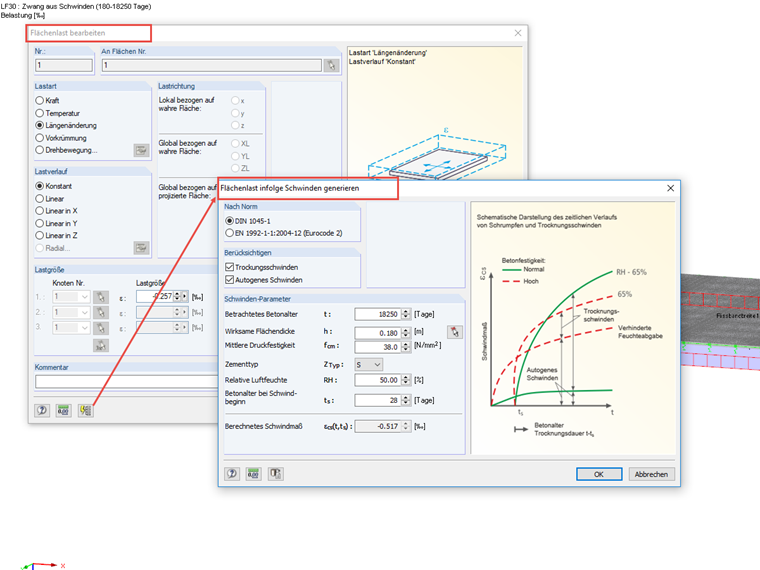
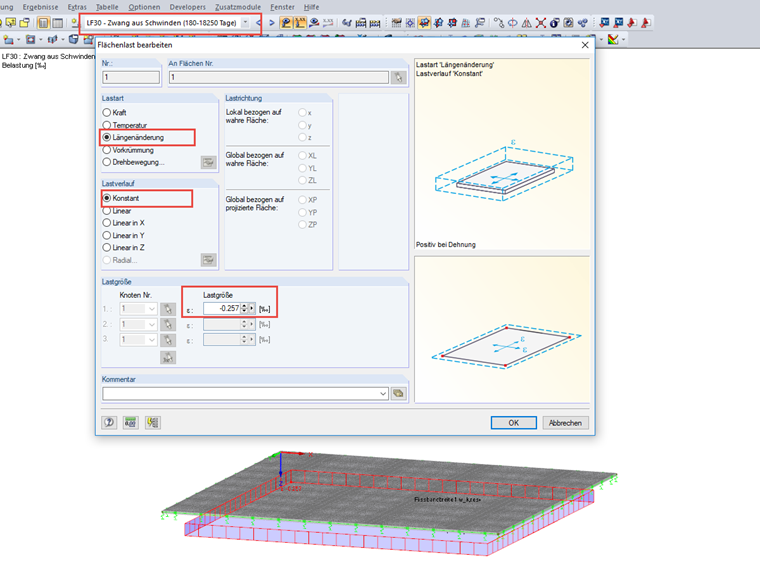
Nach dem Aufbringen der Regallasten/Lagerlasten bilden sich aufgrund der erhöhten Reibungskräfte unter den höheren Regalstielen jedoch Zwangskräfte, die in der Berechnung berücksichtigt werden müssen. Als Zeitpunkt der Aufbringung der Regallasten wird in diesem Projekt t = 180 Tage nach Betonage der Sohlplatte angenommen. Zur Berechnung der Schwinddehnung wird als Schwindbeginn ts = 7 Tage und als Nutzungsende t = 18.250 Tage verwendet. Weiter wird eine relative Luftfeuchtigkeit von 50 % angesetzt. Die Schwinddehnung wird als äußere Flächenlast mittels der Lastart Längenänderung aufgebracht. An dieser Stelle wird darauf hingewiesen, dass im Dialog Flächenlast ein Hilfstool eingebaut ist, welches die Bestimmung der Schwinddehnung sehr komfortabel ermöglicht.
Bei der anzusetzenden Schwinddehnung ist zu berücksichtigen, dass Schwinden bis zum Zeitpunkt t = 180 Tage keine Zwängungen in der Platte verursacht. Daher ist für den Nachweis zum Zeitpunkt t = 18.250 Tage nur die zwangserzeugende Schwinddehnung εcs,wk anzusetzen. Diese errechnet sich als Differenz der Schwinddehnungen bei t = 18.250 und t = 180 Tage. Auf die detaillierte Berechnung der einzelnen Schwinddehnungen wird in diesem Artikel verzichtet.
εcs,wk = εcs (18.250, 7) - εcs (180, 7) = -0,515 ‰ - (-0,258 ‰) = 0,257 ‰
Die zwangserzeugende Schwinddehnung wird als zusätzliche Last definiert und in der Lastkombinatorik für den Zeitpunkt t = 18.250 Tage berücksichtigt.
Für die Nachweise der Gebrauchstauglichkeit wird die Bemessungssituation "Quasi-ständig" benötigt. Dabei wird die veränderliche Last für Lagerräume mit dem Kombinationsbeiwert ψ2 = 0,8 berücksichtigt. Diese Lastkombinationen werden für die Nachweise der Spannungen sowie der Begrenzung der Rissbreite aus Lastbeanspruchung verwendet.
Für die Berücksichtigung der Zwangseinwirkung aus Schwinden zum Nutzungsende (t = 18.250 Tage) werden die zuvor angelegten Lastkombinationen kopiert und jeweils der Lastfall "Schwinden" mit der zwangserzeugenden Schwinddehnung εcs,wk ergänzt. Diese Lastkombinationen werden später für den Nachweis der Rissbreitenbegrenzung unter Lastbeanspruchung mit Zwang verwendet.
Definition der Materialeigenschaften für den Nachweis der Gebrauchstauglichkeit
Für das Abbilden des Materialverhaltens von Stahlfaserbeton eignet sich in RFEM am besten das Materialmodell "Isotrope Beschädigung 2D/3D" des Zusatzmoduls RF-MAT NL. Als Stahlfaserbeton wird ein Beton C30/37 L1,2/L0,9 nach DIN EN 1992-1-1 [2] und DAfStB-Stahlfaserrichtlinie [1] mit den beiden Leistungsklassen L1/L2 = L1,2/L0,9 verwendet. Für eine nichtlineare Berechnung ist auf der Druckseite des Spannungs-Dehnungs-Diagramms der parabolische Verlauf nach 3.1.5 [2] anzusetzen. In Bild 05 wird der charakteristische Verlauf der Arbeitslinie des oben genannten Stahlfaserbetons gezeigt.
Die charakteristische Spannungs-Dehnungs-Linie ist für den Grenzzustand der Gebrauchstauglichkeit anzuwenden. Als Eingabehilfe beziehungsweise Hilfsmittel für die Berechnung der Diagrammpunkte ist diesem Fachbeitrag eine Excel-Datei angehängt. Diese Diagrammpunkte können via Zwischenablage in den RFEM-Eingabedialog übertragen werden (siehe hierzu auch die Empfehlungen im Beitrag zur GZT-Bemessung).
Nachweis des Grenzzustandes der Gebrauchstauglichkeit
Im Zuge des Grenzzustandes der Gebrauchstauglichkeit müssen die Einhaltung der maximal zulässigen
- Grenzspannungen nach 7.2, DIN EN 1992-1-1 [2],
- Rissbreiten nach 7.3, DIN EN 1992-1-1 [2] sowie
- Verformungen nach 7.4, DIN EN 1992-1-1 [2] nachgewiesen werden.
Nach erfolgreicher nichtlinearer Berechnung der Sohlplatte werden die Dehnungen und Spannungen an der Ober- und Unterseite ausgewertet und für die einzelnen Nachweise verwendet.
A) Nachweis der Grenzspannungen
Der Nachweis der maximalen Betondruckspannung nach 7.2 (3) [2] ist erfüllt, wenn unter quasi-ständiger Lasteinwirkung die maximale Betondruckspannung kleiner als 0,45 ⋅ fck bleibt. Hierzu werden die minimalen Spannungen an der Ober- und Unterseite aus der FEM-Berechnung überprüft und mit dem Grenzwert verglichen.
Oberseite:
maximale Druckspannung σ2- = |- 8,5| N/mm² < 0,45 ⋅ fck = 13,5 N/mm²
Unterseite:
maximale Druckspannung σ2+ = |- 3,1| N/mm² < 0,45 ⋅ fck = 13,5 N/mm²
Bild 06 zeigt die maximale Druckspannung an der Oberseite (-z) der Fundamentplatte.
Die Einhaltung der maximalen Betondruckspannung kann somit erfolgreich nachgewiesen werden.
Der Nachweis der Begrenzung der maximalen Betonstahlspannung nach 7.2.(4) und (5) [2] entfällt hier, da keine Betonstahlbewehrung vorhanden ist.
B) Nachweis der Begrenzung der Rissbreiten aus Lastbeanspruchung
Die Nachweisführung der Begrenzung der Rissbreite erfolgt zum Einen für die reine Lastbeanspruchung (zum Zeitpunkt t = 180 Tage) und zum Anderen unter zusätzlicher Berücksichtigung des Zwangs aus Schwinden am Nutzungsende (t = 18.250 Tage). Siehe hierzu auch obige Ausführungen zum Thema Schwinden.
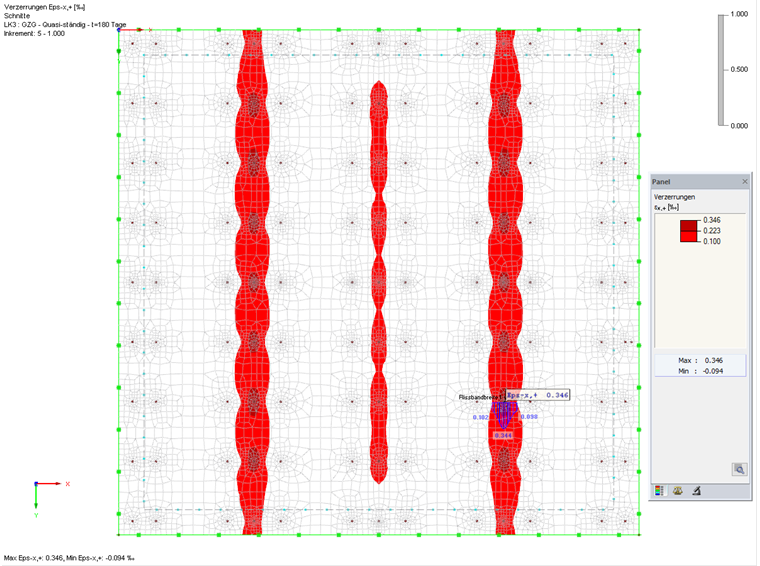
Die Ermittlung der vorhandenen Rissbreite erfolgt auf der Grundlage der quasi-ständigen Einwirkungskombination. Die vorhandene Rissbreite ergibt sich aus der Integration der maßgebenden Dehnungen über die Rissbandbreite. Die Rissbandbreite ist für jede Belastungssituation unterschiedlich und muss manuell aus den Ergebnissen der FEM-Berechnung entnommen werden. Die Rissbandbreite ist rechtwinklig zu der betrachteten Dehnungsrichtung und beinhaltet die Dehnungen, die größer als die Rissdehnung εcr = 0,1 ‰ sind.
Zur Darstellung der Grenzen der Rissbänder in RFEM kann auch das Farbpanel so gesteuert werden, dass nur Dehnungen größer der Rissdehnung angezeigt werden (siehe Bild 07).
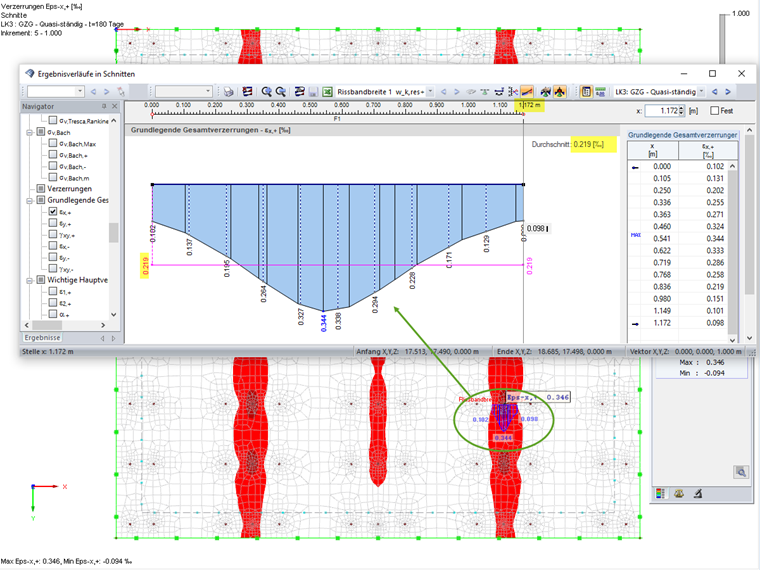
Für die Auswertung der Dehnungen und der Rissbandbreite empfiehlt sich in RFEM das Anlegen eines Schnittes je betrachtetem Rissband. Aus dem Schnitt können sehr einfach die gemittelte Zugdehung und die Rissbandbreite entnommen werden. Dabei muss der Schnitt parallel zur angezeigten Dehungsrichtung definiert werden. Maßgebend in der untersuchten Platte wird die Rissbreite senkrecht zur x-Achse an der Unterseite. Bild 08 zeigt den angelegten Schnitt mit dem Durchschnittswert für die Zugdehnungen und die Integrationslänge.
Die vorhandene Rissbreite wk,vorh aus reiner Lastbeanspruchung (t = 180 Tage) ergibt sich somit zu
wk,vorh,x = 0,219 ‰ ⋅ 1,172 m = 0,26 mm < 0,3 mm (für Expositionsklasse XC 2).
C) Nachweis der Begrenzung der Rissbreiten aus Last- und Zwangsbeanspruchung
Der Nachweis der Rissbreite infolge Last- mit Zwangsbeanspruchung aus Schwinden ergibt sich zum Ende der Nutzungsdauer. Bei der Berechnung der Rissbreite mittels der Verzerrungen aus der FEM–Berechnung ist darauf zu achten, dass die spannungserzeugende Dehnung in einer einfachen Nachlaufberechnung bestimmt wird. Die Erklärung hierfür kann mit dem Schwindverhalten der Platte bis zum Zeitpunkt t = 180 Tage erklärt werden. Wenn sich die Platte zwängungsfrei zusammenziehen kann, ergibt sich in der FEM-Berechnung eine Verzerrung, die gleich der Schwinddehung ist. Die daraus resultierende Spannung ist hier gleich Null. Eine Zugspannung entsteht erst, wenn sich eine sogenannte spannungserzeugende Dehnung εwk,zwang einstellt.
|
εwk,zwang |
spannungserzeugende Dehnung |
|
εFEM |
Dehung aus FEM-Berechung |
|
εcs,wk |
Schwinddehnung |
Um die Rissbandbreite in RFEM bestimmen zu können, muss man sich zuerst die Dehnung des finiten Elements ermitteln, bei der das Element unter der angesetzten Zwangsbeanspruchung reißt.
εcr,FEM,Zwang = εcs,wk + εcr = -0,257 ‰ + 0,1 ‰ = -0,157 ‰
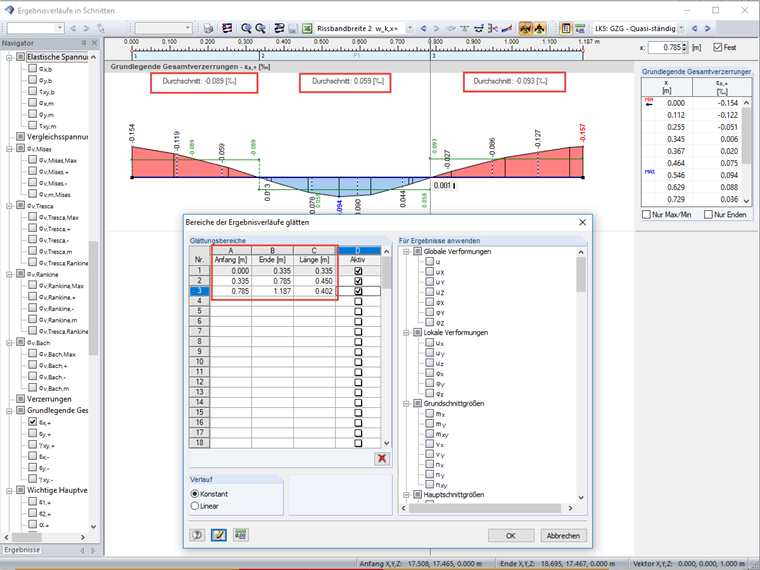
Bild 09 zeigt den maßgebenden Schnitt für die Rissbreitenberechung mit Last- und Zwangsbeanspruchung. Zur Integration der Dehnungen über die Rissbandbreite ist der Schnitt in mehrere Bereiche zu unterteilen.
Die vorhande Rissbreite errechnet sich damit zu
wk,vorh,y = (-0,089 ‰ + 0,257 ‰) ⋅ 0,335 m + (0,059 ‰ + 0,257 ‰) ⋅ 0,450 m + (-0,093 ‰ + 0,257 ‰) ⋅ 0,402 m = 0,27 mm < 0,30 mm (für Expositionsklasse XC 2)
Die Begrenzung der Rissbreiten konnte damit nachgewiesen werden.
D) Nachweis der Verformung
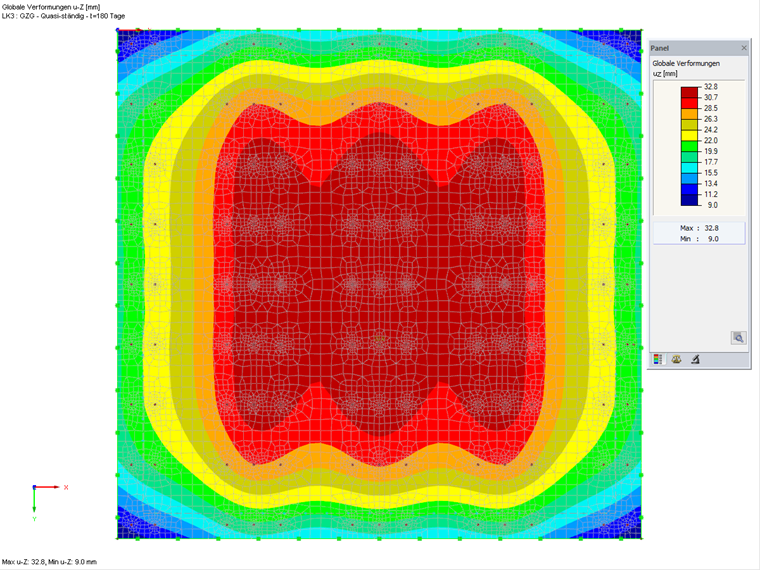
Die maximalen Verformungen können direkt aus den RFEM-Ergebnissen entnommen werden. Die Gesamtverschiebung ergibt sich unter der quasi-ständigen Last zu 32,8 mm. Die Verformungsdifferenz der Sohlplatte ergibt sich aus der Differenz der minimalen und maximalen Verformung und beträgt 32,8 mm - 9 mm = 23,8 mm (siehe Bild 10).
Die zulässigen Grenzwerte und die damit verbundene Systemverträglichkeit für das Regal sind mit dem Regalhersteller abzustimmen.
Abschließend sein noch auf die sehr hilfreichen Empfehlungen für Durchführung von nichtlinearen Berechnungen mit dem Materialmodell "Isotrope Beschädigung 2D/3D" im Fachbeitrag zur Tragfähigkeitsbemessung hingewiesen.