ASCE 7-16 und P-Delta-Effekte
Abschnitt 12.9.1.6 der amerikanischen Norm ASCE 7-16 [1] legt fest, wann P-Delta-Effekte berücksichtigt werden sollten, wenn eine modale Antwortspektrenanalyse für die Erdbebenbemessung durchgeführt wird. Dieser Abschnitt bezieht sich weiter auf Abschnitt 12.8.7 [1], in dem festgehalten ist, dass P-Delta nicht berücksichtigt werden muss, wenn der Stabilitätskoeffizient (θ), der durch die untenstehende Gleichung bestimmt wird, kleiner gleich 0,10 ist.
Dabei ist
Px = gesamte vertikale Bemessungslast im und oberhalb des Stockwerks x, wobei alle Lastfaktoren gleich oder kleiner als 1,0 sind
Δ = Stockwerksverschiebung gemäß Abschnitt 12.8.6 [1], die mit Vx auftritt
Ie = Bedeutungsbeiwert aus Abschnitt 11.5.1 [1]
Vx = seismische Querkraft zwischen den Stockwerken x und x-1
hsx = Geschosshöhe unter dem betrachteten Geschoss x
Cd = Verformungsverstärkungsfaktor aus Tabelle 12.2-1 [1]
Die Norm schreibt weiterhin vor, dass θ den in der folgenden Gleichung angegebenen geringeren Wert von θmax oder 0,25 nicht überschreiten sollte, da die Struktur möglicherweise unsicher ist und neu bemessen werden sollte.
Wenn 0,10 ≤ θ ≤ θmax ist, sollten alle Verschiebungs- und Stabkräfte mit dem folgenden Faktor multipliziert werden:
. Alternativ können P-Delta-Effekte in eine automatisierte Analyse einbezogen werden.NBC 2015 und P-Delta-Effekte
In Abschnitt 4.1.8.4.8.c der kanadischen Norm NBC 2015 [2] wird nur kurz gefordert, dass Schwingungseffekte aufgrund der Interaktion von Auflasten mit der verformten Struktur berücksichtigt werden sollten. Der Kommentar zur NBC 2015 [3] enthält jedoch weitere Erläuterungen, die der Norm ASCE 7 ähneln, wonach der Stabilitätsfaktor (θx) im Stockwerk x mit der unten angegebenen Gleichung berechnet werden sollte.
Dabei ist
ΣWi = Anteil der rechnerischen Eigen- und Nutzlast im Stockwerk x, ermittelt aus S. 4.1.8.11.(7) [3]
ΣFi = Summe der seitlichen seismischen Bemessungskräfte, die im oder über dem Stockwerk x wirken
Ro = Kraftmodifikationsbeiwert aufgrund Überfestigkeit
Δmx = maximale inelastische gegenseitige Stockwerksdurchbiegung, definiert in S. 4.1.8.13.(3) [3]
hs = Zwischengeschosshöhe
Wenn θx kleiner als 0,10 ist, können P-Delta-Effekte ignoriert werden. Wenn θx größer als 0,40 ist, sollte die Struktur neu bemessen werden, da sie bei extremen Erdbeben als unsicher gilt. Für 0,10 ≤ θx ≤ 0,40 können die durch Erdbeben verursachten Kräfte und Momente mit einem Vergrößerungsfaktor von (1+θx) multipliziert werden, um P-Delta zu berücksichtigen. Dieser Vergrößerungsfaktor muss nicht auf Verschiebungen angewendet werden.
Ungefähre Berücksichtigung von P-Delta-Effekten mit Vergrößerungsfaktoren
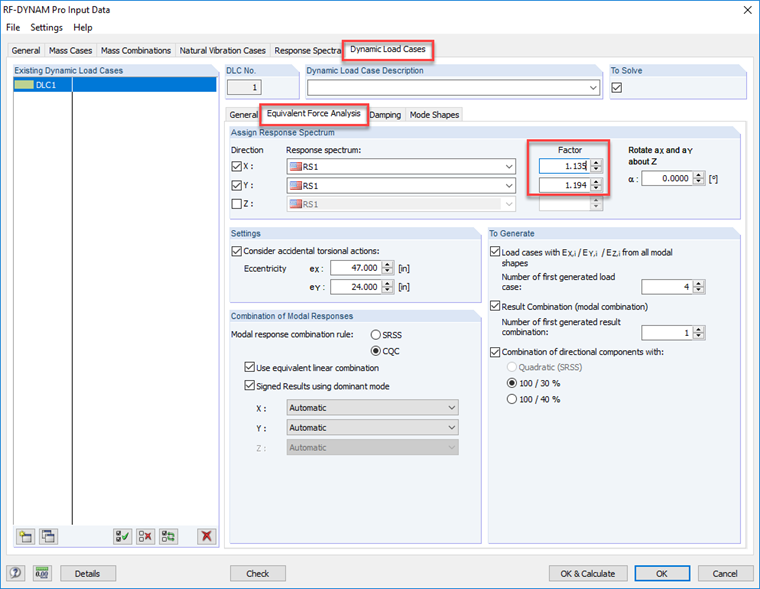
Der Stabilitätsfaktorwert sollte in beiden orthogonalen horizontalen Richtungen berechnet werden, um zu bestimmen, ob P-Delta ein Problem darstellt. Wenn für eine oder beide Richtungen der Einfluss der Theorie II. Ordnung in den angegebenen Bereichen berücksichtigt werden muss, kann der Faktor
aus ASCE 7-16 [1] oder (1 + θx) aus NBC 2015 [3] einfach in RF-/DYNAM Pro - Ersatzlasten herangezogen werden. Alle resultierenden Kräfte und/oder Durchbiegungen werden um den eingestellten Wert verstärkt.
Genauere Berücksichtigung von P-Delta-Effekten mit der geometrischen Steifigkeitsmatrix
Obwohl der Einfluss der Theorie II. Ordnung wie oben beschrieben geschätzt werden kann, ist das ein konservativerer Ansatz. Für Szenarien, in denen große Stockwerksverschiebungen auftreten oder P-Delta-Effekte genauer berechnet werden müssen, kann der Einfluss von Normalkräften in den RF-/DYNAM Pro-Modulen aktiviert werden.
Wenn eine dynamische Analyse durchgeführt wird, sind die typischen nichtlinearen iterativen Berechnungen für Einflüsse aus Theorie II. Ordnung bei Berücksichtigung einer statischen Analyse nicht mehr anwendbar. Das Problem muss linearisiert werden, indem die geometrische Steifigkeitsmatrix während der Berechnung aktiviert wird. Bei diesem Ansatz wird davon ausgegangen, dass sich vertikale Lasten aufgrund horizontaler Effekte nicht ändern und dass die Verformungen im Vergleich zu den Gesamtabmessungen der Struktur gering sind.
Das Konzept hinter der geometrischen Steifigkeitsmatrix ist der Spannungsversteifungseffekt. Axiale Zugkräfte führen zu einer erhöhten Biegesteifigkeit eines Stabes, während axiale Druckkräfte zu einer reduzierten Biegesteifigkeit führen. Dies kann am Beispiel eines Seils oder eines schlanken Stabes leicht demonstriert werden. Wenn der Stab einer Zugkraft ausgesetzt ist, ist die Biegesteifigkeit signifikant größer als wenn der Stab einer Druckkraft ausgesetzt ist. Bei Druck weist der Stab eine sehr geringe oder gar keine Biegesteifigkeit auf, um einer aufgebrachten seitlichen Belastung standzuhalten.
Die geometrische Steifigkeitsmatrix Kg kann aus den statischen Gleichgewichtsbedingungen abgeleitet werden. Vereinfachend werden hier nur die Freiheitsgrade der horizontalen Verschiebung dargestellt.
Die gezeigte Herleitung beruht dem Ansatz des Versatzmomentes auf Basis eines linearen Verschiebungsansatzes. Dies ist für das Biegeelement eine Vereinfachung, beim Fachwerkelement eine exakte Annahme. Es gilt zu beachten, dass die Matrix nur von der Länge des Elements und der Normalkraft abhängt.
Eine genauere Ermittlung der geometrischen Steifigkeitsmatrix für Biegebalken kann unter Verwendung eines kubischen Verschiebungsansatzes oder mit Hilfe der analytischen Lösung der Differentialgleichung der Biegelinie erfolgen. Weitere Informationen zur Theorie und zu den Herleitungen finden Sie bei Werkle [4].
Die geometrische Steifigkeitsmatrix Kg wird der Systemsteifigkeitsmatrix K hinzugefügt und ergibt die modifizierte Steifigkeitsmatrix Kmod:
Kmod = K + Kg
Im Falle von Drucknormalkräften führt dies folglich zu einer Verringerung der Steifigkeit.
Anwendung der geometrischen Steifigkeitsmatrix in RFEM und RF-DYNAM Pro
Die Anwendung der Steifigkeitsreduzierung unter Verwendung der geometrischen Steifigkeitsmatrix zur Berücksichtigung von Einflüssen aus Theorie II. Ordnung (P-Delta) in einer Antwortspektrenverfahren wird teilweise in RFEM und teilweise in RF-DYNAM Pro durchgeführt.
Ein detailliertes Beispiel für den EC 8 finden Sie in der FAQ Wie kann ich die Theorie II. Ordnung bei einer Erdbebenbemessung berücksichtigen? mit PDF zum Download.
Zusätzlich gibt das Dlubal-Webinar ASCE 7-16 Response Spectrum Analysis in RFEM speziell bei 52:25 einen detaillierten Einblick in den Workflow von RFEM und RF-DYNAM Pro für die Anwendung der geometrischen Steifigkeitsmatrix zur Berücksichtigung von P-Delta-Effekten nach ASCE 7.