DUENQ | Kaltgeformte Profile

Feature

Zurück zu Features

Kaltgeformte Profile nach EN 1993-1-3 mit Dlubal Software

01
Programm DUENQ 9 | Wirksamer Querschnitt eines kaltgeformten Z-Profiles

Zurück zu Features

4. Februar 2020

001410

DUENQ ermittelt für kaltgeformte Profile die wirksamen Querschnitte nach EN 1993-1-3 und EN 1993-1-5. Die in EN 1993-1-3, Abschnitt 5.2 genannten geometrischen Verhältnisse zur Anwendbarkeit der Norm können optional überprüft werden.

Die Auswirkungen des lokalen Plattenbeulens werden nach der Methode der reduzierten Breiten und das mögliche Ausknicken der Steifen (Forminstabilität) wird bei versteiften Profilen gemäß EN 1993-1-3, Abschnitt 5.5 berücksichtigt.

Optional kann eine iterative Berechnung zur Optimierung des wirksamen Querschnitts vorgenommen werden.

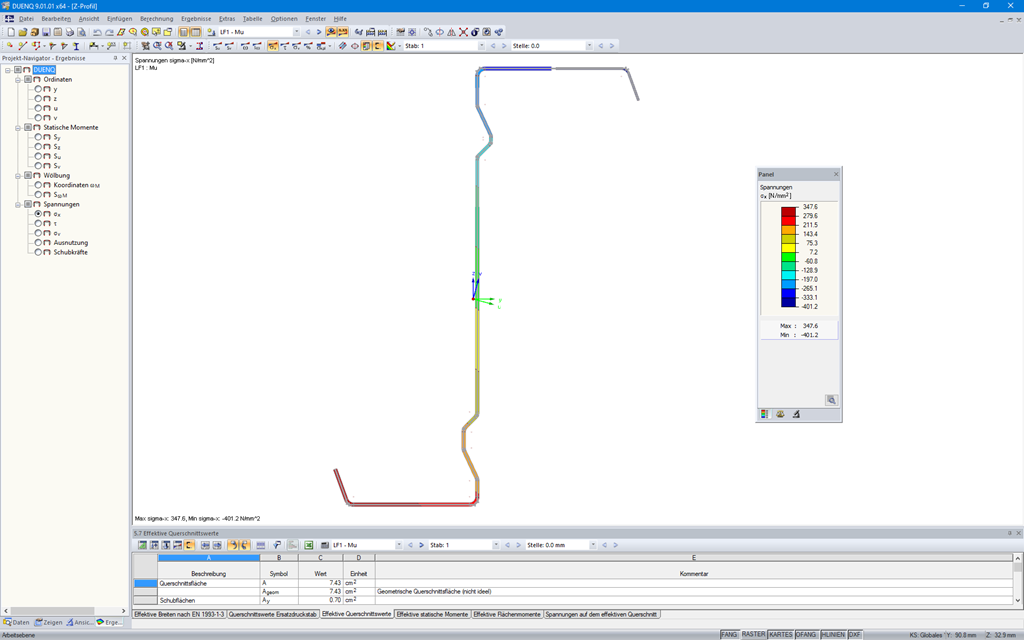
Die wirksamen Querschnitte lassen sich grafisch darstellen.

Im Fachbeitrag "Nachweis eines dünnwandigen, kaltgeformten C-Profils nach EN 1993-1-3" wird die Bemessung von kaltgeformten Profilen mit DUENQ und RF-/STAHL Kaltgeformte Profile ausführlich beschrieben:

Nachweis eines dünnwandigen, kaltgeformten C-Profils nach EN 1993-1-3

Mehr über RF-/STAHL Kaltgeformte Profile

Schreiben Sie einen Kommentar...

0 Kommentieren

0 0

RFEM 6 | Die neue Statiksoftware

Gehe zu
Events
Videos
Modelle
Knowledge Base
Screenshots
Produkt-Features
Häufig gestellte Fragen
Kundenprojekte

Empfohlene Veranstaltungen

Pneumatische Membrankonstruktionen in RFEM 6

Formfindung und Berechnung von pneumatischen Membrankonstruktionen in RFEM 6

Webinar 4. April 2023 14:00 - 15:00 CEST

Formfindung und Berechnung pneumatischer Membranstrukturen in RFEM 6

Webinar 6. April 2023 14:00 - 15:00 CEST

Eurocode 3 | Stahlbau nach DIN EN 1993-1-1

Online-Schulung 16. Mai 2023 8:30 - 12:30 CEST

Eurocode 3 | Stahltragwerke nach DIN EN 1993-1-1

Online-Schulung 23. Mai 2023 8:30 - 12:30 CEST

Stahlsilobemessung in RFEM 6 (USA)

Webinar 21. März 2023 14:00 - 15:00 EDT

Analyse von Stahlkonstruktionen in RFEM 6 und RSTAB 9

Webinar 9. März 2023 14:00 - 15:00 CET

Analyse von Stahlkonstruktionen in RFEM 6 und RSTAB 9

Webinar 7. März 2023 14:00 - 15:00 CET

Eurocode 3 | Stahltragwerke nach DIN EN 1993-1-1

Online-Schulung 2. März 2023 9:00 - 13:00 CET

Eurocode 3 | Stahltragwerke nach DIN EN 1993-1-1

Online-Schulung 28. Februar 2023 8:30 - 12:30 CET

Stahlbemessung nach CSA S16:19 in RFEM 6 (USA)

Webinar 15. Februar 2023 14:00 - 15:00 EDT

Stabilitäts- und Wölbkrafttorsionsanalysen in RFEM 6 und RSTAB 9

Webinar 26. Januar 2023 14:00 - 15:00 CET

Stabilitäts- und Wölbkrafttorsionsanalysen in RFEM 6 und RSTAB 9

Webinar 24. Januar 2023 14:00 - 15:00 CET

Weitere Veranstaltungen

Videos

Kaltgeformte Profile nach EN 1993-1-3 mit Dlubal Software

Länge 1:43 min

[EN] Designing Cold-Formed Steel Sections According to Eurocode 3

Länge 36:11 min

Bemessung kaltgeformter Stahlprofile nach Eurocode 3

Länge 45:33 min

KB 001629 | Nachweis eines dünnwandigen, kaltgeformten C-Profils nach EN 1993-1-3

Länge 4:41 min

Webinar | Stahlsilobemessung in RFEM 6

Länge 1:04:40 min

Plastisches Materialmodell für die Schweißnahtbemessung

Länge 0:39 min

Stabtyp "Flächenmodell"

Länge 0:39 min

Nachweise für kaltgeformte Stahlstäbe nach EN 1993-1-3

Länge 0:53 min

KB 001808 | CSA S16:19 Berücksichtigung von Stabilität und Neuer Anhang O.2

Länge 2:18 min

Weitere Videos

Modelle zum Herunterladen

Beiträge aus der Knowledge Base

System und Belastung (Abmessungen in mm, Kraft in kN)

Nachweis eines dünnwandigen, kaltgeformten C-Profils nach EN 1993-1-3

Der Tragfähigkeitsnachweis für kaltgeformte Profile nach EN 1993-1-3 und EN 1993-1-5 kann mit der Modulerweiterung RF-/STAHL Kaltgeformte Profile geführt werden.