Was bedeutet Zug für ein Betonelement?
Der Querschnitt eines Bauteils ist rein zugbeansprucht, wenn die Kräfte, die auf eine Seite des Profils wirken, im Schwerpunkt des Querschnitts auf eine einzige Kraft N reduziert sind. Diese Normalkraft N steht also senkrecht zum Querschnitt und ist auf die Seite gerichtet, an der die Kräfte wirken. Das Eigengewicht wird im Beton vernachlässigt und der Querschnitt steht gleichmäßig unter Zug.
Zugspannung im Stahl
Bei Stahl mit ansteigendem Ast im Spannungs-Dehnungs-Diagramm wird die Gleichung rechts vom Ast, die dem Zugverhalten von Stahl entspricht, entsprechend der charakteristischen Werte des Stahls gemäß §3.2.7 (2) in EN 1992-1-1 beschrieben.
| σS | Spannung in Bewehrung |
| fyd | Bemessungswert der Streckgrenze = fyk / γs |
| k | Verhältnis der charakteristischen Grenzwerte = ftk / fyk |
| εuk | Grenzverformung |
| Es | Elastizitätsmodul |
| εS | Verformung des Bewehrungsstahls = εud = 0.9 ⋅ εuk |
| fyk | Charakteristische Streckgrenze |
| γS | Teilsicherheitsbeiwert des Stahls |
| ftk | Charakteristischer Wert der Zugfestigkeit |
| εud | Bemessungswert der Grenzverformung |
Längsbewehrung
Zur Erinnerung: der Beton unter Zug wird für reinen Zug vernachlässigt. Somit gleicht nur der Stahl die Zugkraft Ned vollständig aus. Der erforderliche Bewehrungsquerschnitt wird dann entsprechend der Zugkraft und der vorhandenen Spannung ermittelt.
As = NEd / σs
AS ... Fläche des Bewehrungsquerschnitts
NEd ... Grenznormalkraft
Anwendung der Theorie mit dem Zusatzmodul RF-BETON Stäbe
Als Beispiel untersuchen wir ein Element, das mit einfachem Zug beansprucht ist, indem die für die Längsbewehrung erhaltenen Ergebnisse betrachtet werden. Nachfolgend sind die Eingabedaten aufgelistet:
- Ständige Lasten: Ng = 100 kN
- Veränderliche Lasten: Nq = 40 kN
- Quadratischer Querschnitt: 20/20 cm
- Betonfestigkeitsklasse: C25/30
- Stahl: S 500 A bei ansteigendem Ast
- Durchmesser der Längsbewehrung: ϕl = 12 mm
- Durchmesser der Querbewehrung: ϕt = 6 mm
- Betondeckung: 3 cm
- Eine Kontrolle der Rissbildung ist nicht erforderlich.
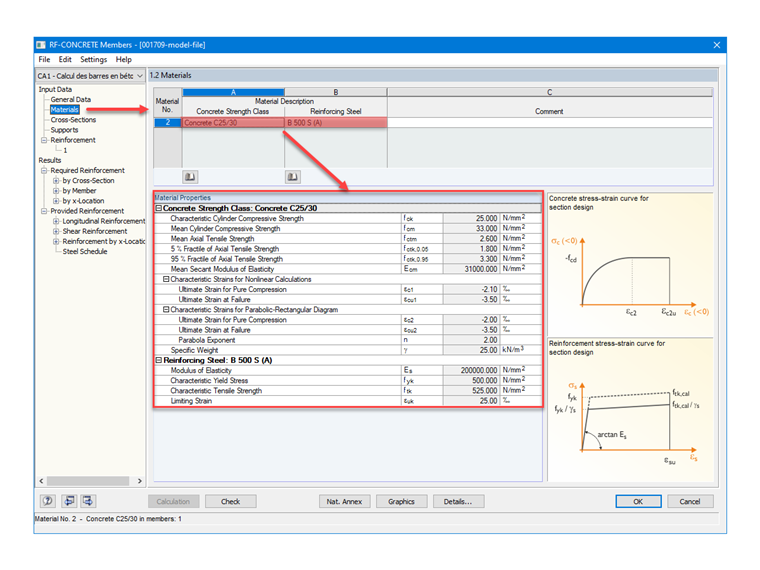
Zur Überprüfung der Materialeinstellungen in RF-BETON Stäbe sind in Bild 02 die verwendeten Materialien für Beton und Bewehrung dargestellt.
Grenzzustand der Tragfähigkeit
Beanspruchungen im Grenzzustand der Tragfähigkeit:
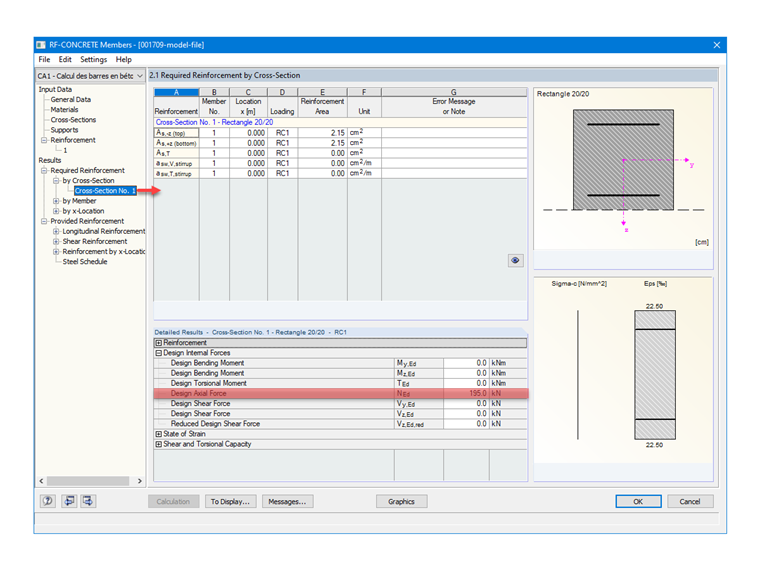
NEd = 1,35 ⋅ 100 + 1,5 ⋅ 40 = 195,00 kN
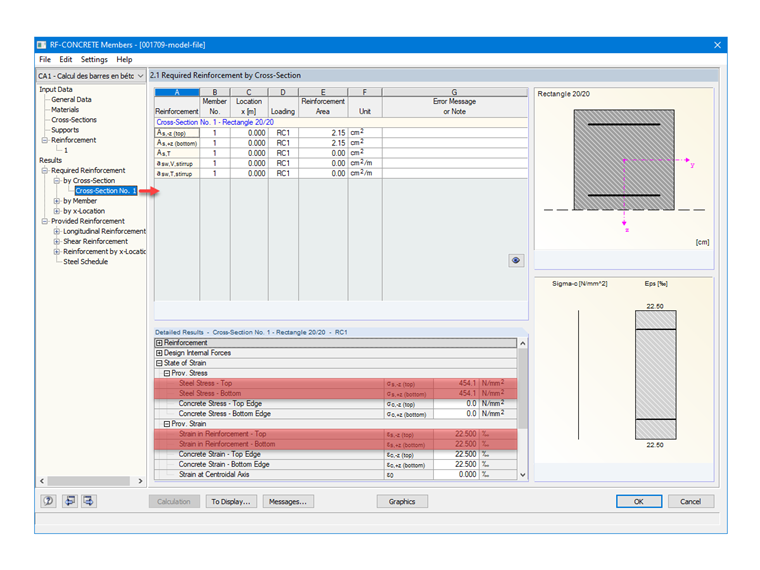
Vorhandene Zugspannung
Grenzzustand der Tragfähigkeit bei einer dauerhaften, vorübergehenden Bemessungssituation:
fyd = 500 / 1,15 = 435 MPa
k = 525 / 500 = 1,05 gemäß Tabelle C.1 des EN 1992-1-1
εuk = 25 ‰
εud = 0,9 ⋅ 25 = 22,5 ‰
σs = 435 + (1,05 ⋅ 435 - 435) / (2,5 - 435 / (200 000)) ⋅ [2,25 - 435 / (200 000)] = 454 MPa
Erforderliche Längsbewehrung
Längsbewehrung für den Grenzzustand der Tragfähigkeit:
As = 0,195 / 454 ⋅ 104 = 4,30 cm²
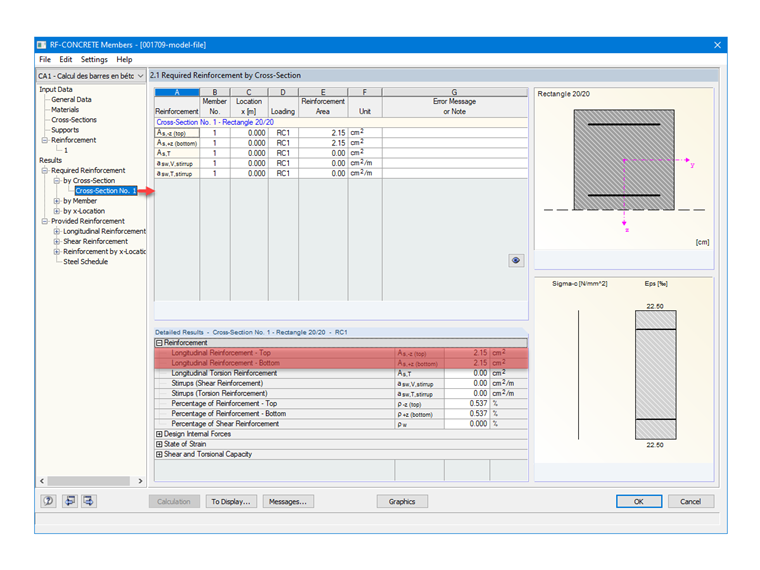
Vorhandene Längsbewehrung
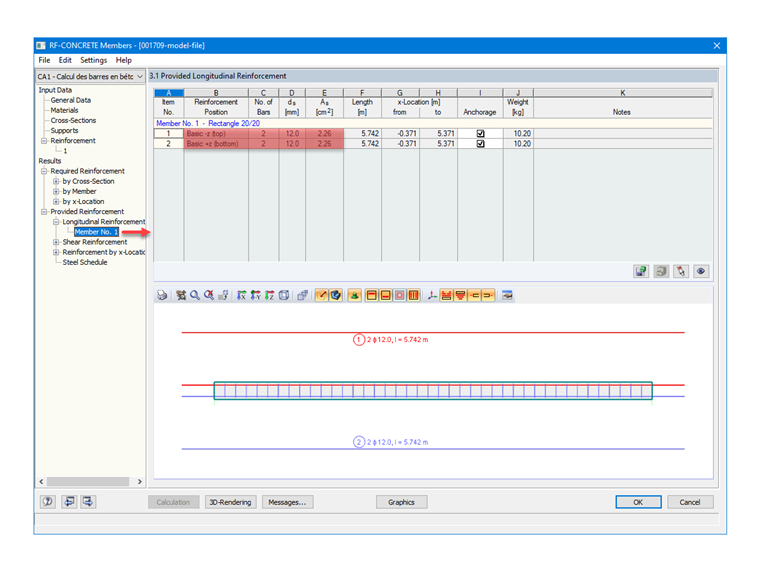
Nachdem der Stahl mit einem Durchmesser von 12 mm in RF-BETON Stäbe eingestellt wurde, entspricht die automatisch ermittelte vorhandene Bewehrung 4 Bewehrungsstäben, mit einer symmetrischen Verteilung auf die unteren und oberen Teile des Profils, hier 2 x 2 HA12, was folgende Bewehrungsquerschnittsfläche ergibt:
As = 4 ⋅ 1,13 = 4,52 cm²
Querbewehrung
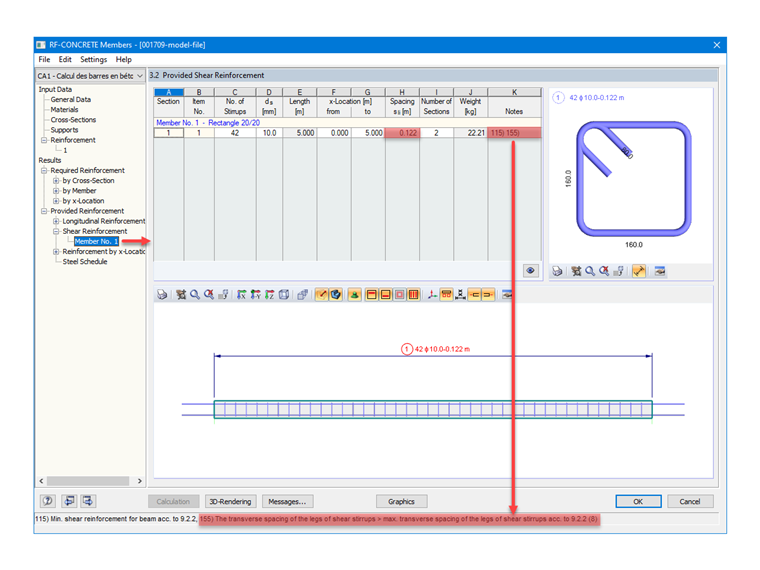
Da die Querbewehrung auch vom Anwender festgelegt wird, kann RF-BETON Stäbe die Abstände automatisch nach Norm ermitteln und überprüfen, ob die Anordnung dieser übereinstimmt.
In unserem Fall liefert uns das Programm durch das Einlegen von Bügeln mit einem Durchmesser von 6 mm einen Abstand von 0,122 m, zeigt uns aber auch in der Hinweisspalte die Warnmeldung Nr. 155), wie Bild 07 zeigt.
Die Formel, die sich auf § 9.2.2 (8) in EN 1992-1-1 bezieht, ist im Folgenden definiert.
Sl,max = 0,75 ⋅ d
Sl,max ... maximaler Querabstand der Bügel
d ... Effektive Höhe
d = h - e - ∅t - ∅l/2
h ... Profilhöhe
e ... Betondeckung
Die oben aufgeführten Formeln liefern folgende Ergebnisse:
d = 0,200 - 0,03 - 0,006 - 0,012 / 2 = 0,158 m
Sl,max = 0,75 ⋅ 0,158 = 0,12 m
Daher erscheint die Warnung 155, da der Abstand der Bügelschenkel eines Trägers in Querrichtung den Grenzwert der Norm überschreitet. Das Problem kann gelöst werden, indem die Schnittigkeit der Bügel in den Einstellungen der Bügelbewehrung erhöht wird, wie in dieser FAQ beschrieben.
Fazit
Nachdem die Parameter zunächst vorgegeben werden, gibt RF-BETON Stäbe die Anzahl der erforderlichen Bewehrungen gemäß der festgelegten Anordnung an, um die Zugbeanspruchung entsprechend der von RFEM gelieferten Schnittgrößen nachzuweisen. Je nach angezeigter Warnmeldung ist es dem Anwender auch möglich, die Bewehrungen und deren Anordnung nach der Berechnung zu ändern.
