Vlastní frekvence

Kategorie výsledkové tabulky Vlastní frekvence obsahuje vlastní frekvence netlumeného systému. V záhlaví tabulky lze přepínat mezi výsledky modálních zatěžovacích stavů.

Kategorie výsledku 'Vlastní frekvence' pro modální analýzu

Každá frekvence systému má svůj vlastní tvar. Tvary režimů se zobrazují také graficky (viz obrázek # extbookmark manual|image027573|Výsledky modální analýzy #). V navigátoru vyberte vlastní tvar nebo použijte tlačítka a pro přepínání mezi vlastními tvary (viz obrázek # extbookmark manuál|image027595|Vyberte režim tvar #). Pro zobrazení určitého tvaru režimu v pracovním okně lze také vybrat příslušný řádek v tabulce.

Vlastní frekvence

Tabulka 'vlastní frekvence' (viz obrázek image027927 kategorie výsledků 'vlastní frekvence' ) poskytuje přehled o následujících výsledcích netlumeného systému:

• Vlastní čísla
• vlastní úhlová frekvence
• Vlastní frekvence
• Vlastní perioda

Pohybová rovnice systému s více stupni volnosti bez tlumení je dána zadaným # extbookmark manual|eigenvalue-solver|Metoda řešení # vypočítaná.

M závisí na typu # extbookmark manual|mass-matrix|Matice hmot #.

Vlastní číslo λ [1/s²] je spojeno s úhlovou frekvencí ω [rad/s], přičemž λ_i = ω_i². Vlastní frekvence f [Hz] se pak odvodí pomocí f = ω/(2π). Vlastní perioda T [s] je převrácená hodnota frekvence, která se stanoví pomocí T = 1/f.

Pro systém s několika stupni volnosti (MDOF) existuje několik vlastních čísel λ_i a souvisejících vlastních tvarů u_i .

Účinné modální hmoty

Tabulka modálních hmotností

Záložka 'Účinné modální hmoty' obsahuje přehled následujících výsledků:

• Modální hmotnost M_i
• Účinná modální hmotnost pro translační směry m_eX, m_eY, m_eZ
• Vzpěrná modální hmotnost pro směry otáčení m_eφX, m_eφY, m_eφZ
• Součinitel efektivní modální hmotnosti pro translační směry f_meX, f_meY, f_meZ
• Součinitel efektivní modální hmotnosti pro směry otáčení f_mφX, f_mφY, f_mφZ
• Součty výsledků

Efektivní modální hmoty popisují, kolik hmoty se aktivuje v každém směru každým vlastním tvarem systému.

Modální hmotnost je definována následovně:

Vlastní vektor u_i vlastního tvaru i je uveden v rovnici vzorec001058 vlastní tvary . M závisí na typu # extbookmark manual|mass-matrix|Matice hmot #.

Modální hmota M_i je nezávislá na směru. Mění se však v závislosti na změně měřítka tvarů režimu .

Efektivní modální hmoty m_ij^eff popisují hmoty, které jsou zrychlené ve směru j, kde j = 1, 2, 3 pro posun a j = 4, 5, 6 pro rotaci - pro každý jednotlivý vlastní tvar i. Tyto hmoty jsou nezávislé na změně měřítka tvarů . Jsou přímo vztaženy k TABLE_PARTICIPATION_FACTORS participačním faktorům Γ_{i, j} (viz rovnice vzorec001060 participační faktor ).

Pro každý uzel KP existuje matice T.

Účinné modální hmoty se definují následovně:

Součet účinných modálních hmotností ∑m_e je uveden na konci tabulky. V translačních směrech se tyto součty rovnají celkové hmotnosti konstrukce ∑_M. Výjimkou jsou hmoty, které nejsou aktivovány, například hmoty v pevných podporách. Plné hmotnosti se dosáhne pouze tehdy, když se spočítají všechna vlastní čísla modelu.

Na základě součinitele efektivní modální hmotnosti f_me je třeba rozhodnout, zda je třeba pro metodu spektra odezvy zohlednit určitý tvar. Například EN 1998-1, odstavec 4.3.3.3 stanoví, že „součet efektivních modálních hmotností uvažovaných modálních příspěvků činí nejméně 90 % celkové hmotnosti konstrukce“ a že „se berou všechny modální příspěvky zohlednit, jejichž efektivní modální hmotnosti tvoří více než 5 % z celkového množství hmot“.

Součinitele efektivní modální hmotnosti f_me zadáme následovně:

Další informace o modální analýze a součinitelích efektivní modální hmotnosti viz Meskouris Viz [2 ] a Tedesco Viz [3 ].

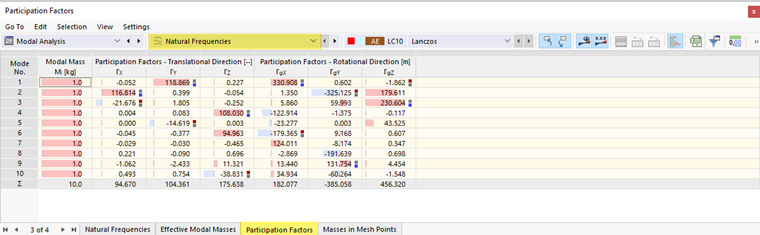
Součinitele kombinace

Tabulka 'Participační faktory'

V záložce 'Participation Factors' jsou uvedeny následující výsledky:

• Modální hmotnost M_i
• Součinitel účasti pro translační směry Γ_X, Γ_Y, Γ_Z
• Součinitel účasti pro směry otáčení Γ_φX, Γ_φY, Γ_φZ
• Součty výsledků

Součinitel spoluúčasti je definován následovně:

Součinitele spoluúčasti, které definují také stupně volnosti pootočení, jsou blíže popsány v Viz [1 ]. Účastnický součinitel Γ_{i, j} je pro posuny bezrozměrný; pro rotace má jednotku [m].

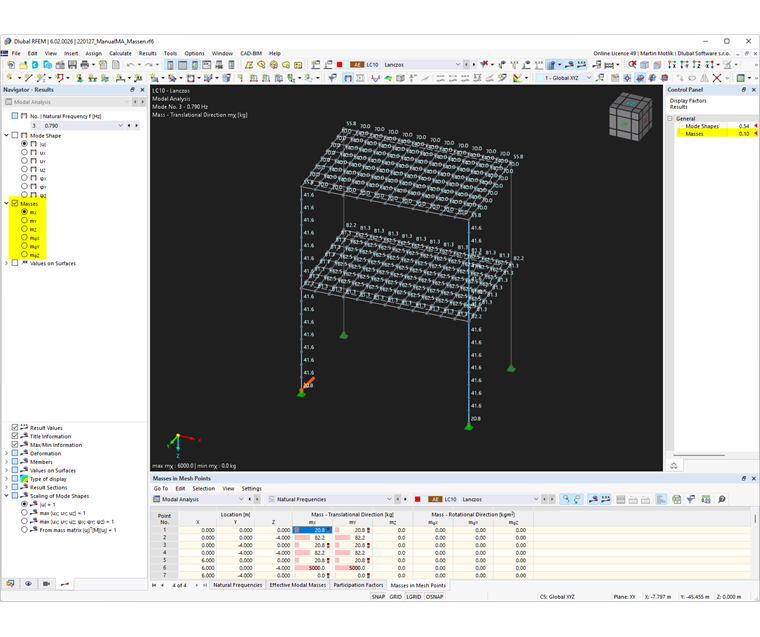
Hmoty v bodech sítě prvků

Tabulka 'Hmotnosti v bodech sítě'

V registru 'hmotnosti v bodech sítě' jsou uvedeny následující výsledky:

• Rozměry pro translační směry m_X, m_Y, m_Z
• Hmotnost pro směry otáčení m_φX, m_φY, m_φZ
• Součty hmotností

Tyto hodnoty představují hmoty, které byly přiřazeny v zatěžovacím stavu pro modální analýzu a použity při výpočtu na uzly sítě konečných prvků. Závisí také na nastavení modální analýzy . Další informace naleznete v kapitole Hmoty .

Součet hmotností pro každý směr je uveden na konci tabulky.

Hmoty v bodech sítě lze graficky zobrazit na modelu. K tomu slouží kategorie Hmota v navigátoru.

Grafické znázornění hmot mx

V # extbookmark manuálu|resultFactorsTab|Pomocí ovládacího panelu # lze upravit součinitele převýšení pro grafické znázornění hmot.