Odkształcenia plastyczne reprezentują właściwości materiału, które wymagają analizy nieliniowej. Sie kann in RFEM im Zusammenspiel mit dem Zusatzmodul RF-MAT NL erfolgen, um ein elastisch-plastisches Materialverhalten bei der Analyse zu berücksichtigen.
Als Verzerrungshypothesen stehen hierzu neben der Fließbedingung nach von Mises die Ansätze nach Tresca, Drucker-Prager und Mohr-Coulomb zur Auswahl. Für duktile Materialien wie Stahl empfiehlt sich die Plastizitätstheorie nach von Mises. Sie lautet für den allgemeinen räumlichen Spannungszustand:
Nähere Informationen zu den Spannungshypothesen finden sich unter folgenden Links:
- Instrukcja programu RFEM 5 | 8.22 Powierzchnie - naprężenia zastępcze
- Wikipedia | Napięcie równoważne
Anhand eines einfachen Modells mit uniaxialer Belastung werden die Möglichkeiten plastischer Untersuchungen mit RFEM und RF-MAT NL vorgestellt.
Beispiel Zugprüfkörper
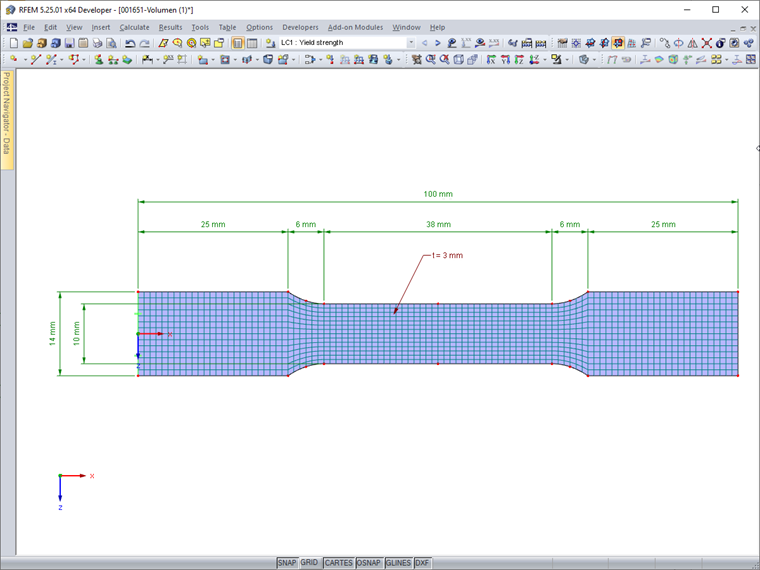
Ein Zugprüfköper aus Stahl S 235 mit den in Bild 01 dargestellten Abmessungen ist an einem Ende eingespannt. Das Modell wird als Fläche mit 2D-Elementen erstellt.
Wegen der sehr kleinen Abmessungen des Prüfkörpers wird eine FE-Netzgröße von 1 mm gewählt. Es sollen nur die Spannungen infolge einer Zugbeanspruchung nach Theorie I. Ordnung untersucht werden; eine Stabilitätsanalyse unterbleibt.
Zugbeanspruchung bis zur Streckgrenze
Die Kraft, die zum Erreichen der Streckgrenze erforderlich ist, bestimmt sich für das Modell wie folgt:
N = fy · A = 235 N/mm² · (10 mm · 3 mm) = 7.050 N
Sie wird am Ende des Prüfkörpers als Linienlast aufgebracht:
7.050 N / 14 mm = 503,57 N/mm = 503,57 kN/m
Der Lastfall 1 wird zunächst mit dem Standard-Materialmodell isotrop linear-elastisch nach Theorie I. Ordnung berechnet. Ciężar własny nie jest uwzględniany.
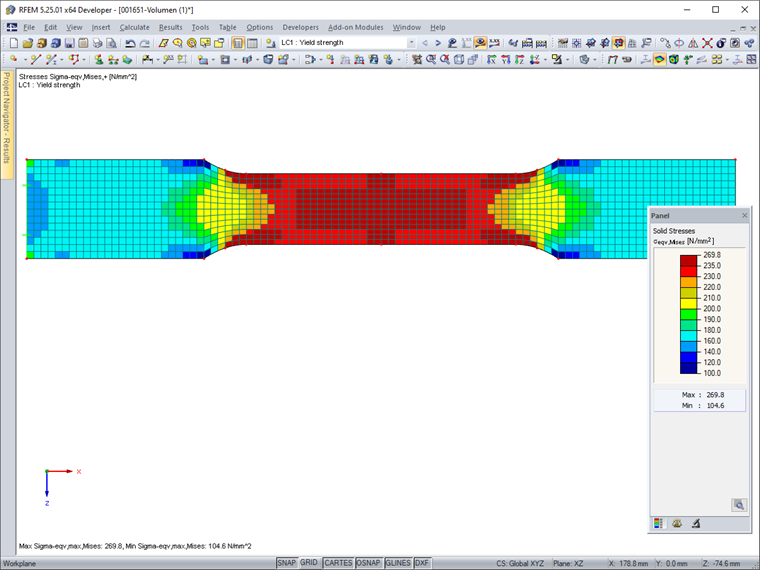
Zur Darstellung der Vergleichsspannungen nach von Mises wird der Ergebnisverlauf "Konstant in Elementen" gewählt. Damit erfolgt keine Glättung über die Elementgrenzen hinweg. In Bild 02 ist erkennbar, dass die Fließspannung von 235 N/mm² in Bereichen des reduzierten Querschnitts überschritten ist. Die Ergebnisse spiegeln daher nicht die Spannungsverläufe einer Zugprüfung mit Fließeffekten wider.
Für eine realitätsnahe Berechnung eignet sich das Materialmodell "Isotrop plastisch 2D/3D", das mit einer Lizenz für <nobr>RF-MAT NL</nobr> genutzt werden kann. Ten model materiałowy odwzorowuje zachowanie się materiału izotropowego w strefie sprężystej. Der plastische Bereich basiert auf den Fließbedingungen der Verzerrungshypothese nach von Mises mit einer Fließgrenze der Vergleichsspannung von 235 N/mm². Die Berechnung erfolgt iterativ in mehreren Lastschritten. Hierzu wird die Option "Anzahl der Laststeigerungen zur automatischen Ermittlung durch die Newton-Raphson-Methode" genutzt, die bei den RFEM-Berechnungsparametern für Materialien mit nichtlinearem Modell aktiviert werden kann. Damit ist die erforderliche Genauigkeit der Ergebnisse bei einer relativ kurzen Berechnungsdauer gewährleistet.
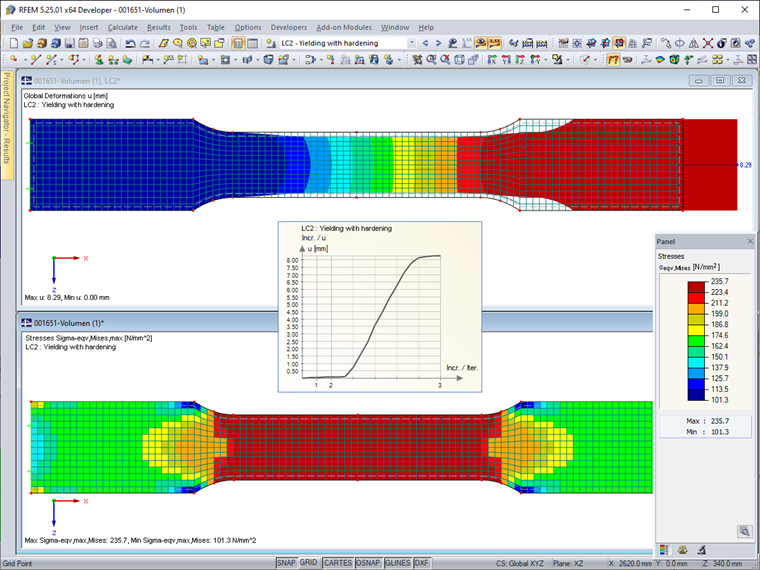
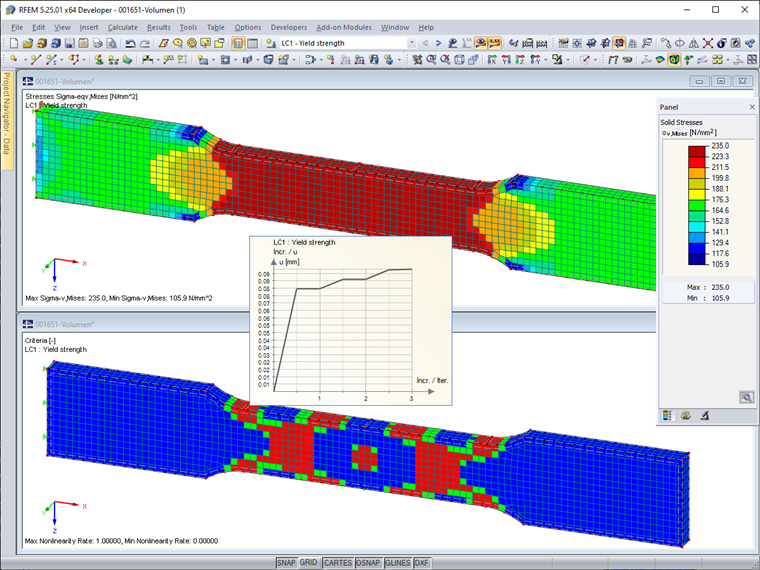
Bild 03 zeigt die Spannungen und den Nichtlinearitätsgrad (Anteil der Elemente mit Fließen) des nichtlinearen Materialmodells. Die Streckgrenze von 235 N/mm² wird in keinem Element überschritten. Im Berechnungsdiagramm ist der Verformungsverlauf während der Iterationen ablesbar.
Lasterhöhung und Fließen
Im LF 2 wird die "Fließlast" von 503,57 kN/m geringfügig auf 505,00 kN/m gesteigert. Die Berechnung liefert eine ausgeprägte Gesamtdehnung des Prüfkörpers von 8,29 mm (zum Vergleich: 0,10 mm im LF 1). Es stellt sich aber noch eine Konvergenz ein, die nicht zuletzt auch auf den Verfestigungsmodul Ep = 2,1 N/mm² zurückzuführen ist (siehe Fachbeitrag
KB001479 | Parametry hartowania w nieliniowych modelach materiałowych
). Der geschwächte Bereich des Querschnitts befindet sich komplett im Fließzustand.
Bei der elastisch-plastischen Berechnung wird die Gesamtdehnung ε in eine elastische Komponente εel und eine plastische Komponente εpl aufgeteilt:
ε = εel + εpl
Diese Aufteilung ist jedoch nur gültig unter der Annahme, dass die plastischen Dehnungen gering sind. Hier kann als Faustwert εpl < 0,1 angenommen werden (siehe COMSOL® Learning Center). Werden die plastischen Dehnungen zu groß, so sind die plastischen Ergebnisse mit Vorsicht zu bewerten.
Die Längenänderung im verjüngten Bereich (Annahme: l = 38 mm) infolge elastischer Dehnung ist:
εel = σ / E = 235 N/mm² / 210.000 N/mm² = 0,00119
∆lel = 0,00119 · 38 mm = 0,04 mm
Diese Verformung ist auch in Tabelle "4.2 Knotenverformungen" aus der Differenz der Verschiebungen uX der Knoten 4 und 5 im LF 1 überprüfbar.
Im LF 2 ergibt sich aus den Verschiebungen dieser Knoten folgende plastische Dehnung:
εpl = (∆ltot - ∆lel) / l = (8,24 mm - 0,05 mm - 0,04 mm) / 38 mm = 0,21 > 0,1
Damit sind die Grenzen des nichtlinearen Materialmodells überschritten. Zum Vergleich erfolgen weitere Untersuchungen an einem 3D-Modell des Zugprüfkörpers, das die räumliche Komponente in einem Volumenmodell erfasst.
Model bryłowy
Die Vernetzung des 3D-Modells erfolgt ebenfalls mit einer Maschenweite von 1 mm. Damit ergeben sich drei finite Volumenelemente über die Querschnittsdicke.
Die Kraft von 7.050 N, die zum Erreichen der Streckgrenze erforderlich ist (siehe oben), wird am Ende des Prüfkörpers als Flächenlast aufgebracht. Sie ermittelt sich wie folgt:
7.050 N / (14 mm · 3 mm) = 167,857 N/mm² = 167.857 kN/m²
Wie Bild 05 zeigt, bestätigen die Volumen-Vergleichsspannungen und der Nichtlinearitätsgrad des LF 1 die Ergebnisse des Flächenmodells.
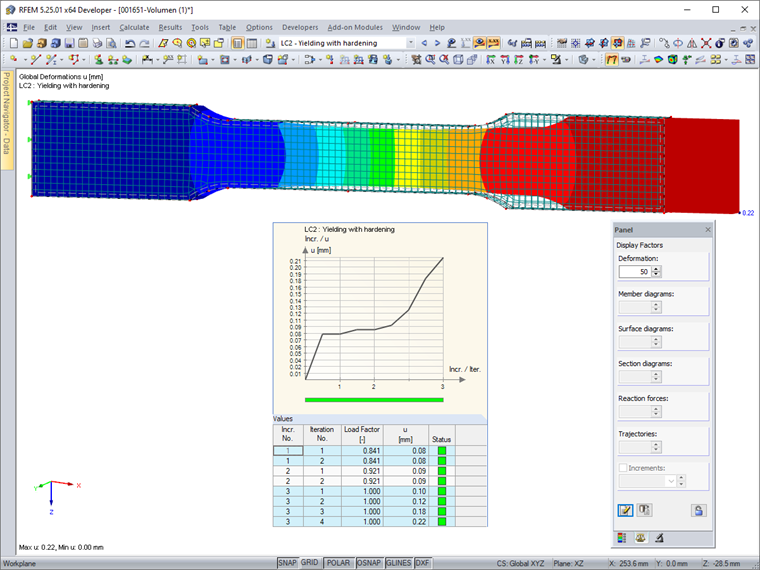
Die Berechnung des LF 2 - mit einer äquivalenten Flächenlast von 168.333 kN/m² - liefert im Volumenmodell eine geringere Gesamtverformung von 0,22 mm als im Flächenmodell mit 8,29 mm. Im Berechnungsdiagramm sind jedoch die nichtlinearen Effekte des Materialfließens ebenfalls deutlich erkennbar.
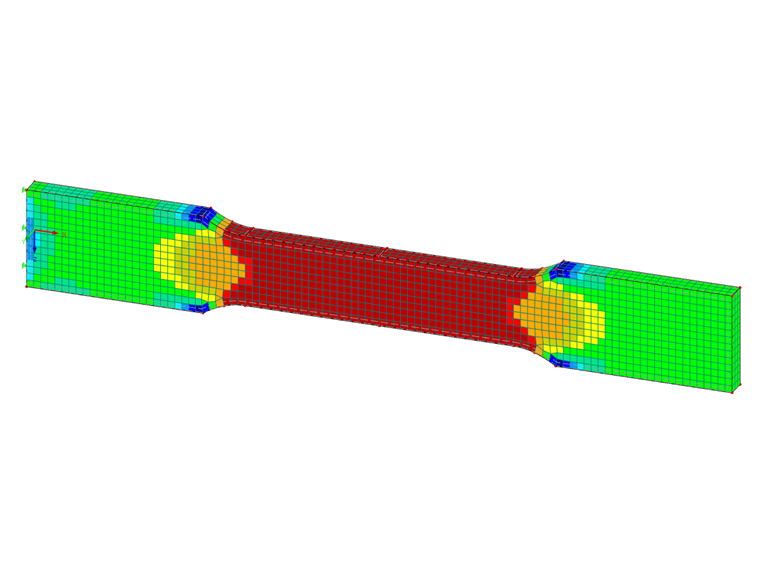
Wie Bild 06 zeigt, spiegelt die Verformungsfigur (in überhöhter Darstellung) den Beginn der Einschnürung einschließlich Querverformung wider.
Das Volumenmodell stellt somit eine interessante Alternative zur Abbildung des Fließprozesses dar. Erst eine Last von etwa 177.900 kN/m² würde hier zur Verformung von 8,29 mm des LF 2 im Flächenmodell führen. Dies entspricht einer Erhöhung der Streckgrenz-Last um 6 % (Flächenmodell: 0,3 %).
Der Abgleich des Modells mit dem realen Materialverhalten könnte letztendlich durch eine entsprechende Versuchsanordnung mit Zugprüfung erfolgen.
Podsumowanie
Anhand eines einfachen Beispiels wurde vorgestellt, wie nichtlineare Materialgesetze in RFEM abgebildet und untersucht werden können. Die Modellierung ist sowohl über Flächen- als auch Volumenelemente möglich. Das Volumenmodell ist prinzipiell zu empfehlen, wenn der Einfluss der Elementdicke zum Tragen kommt. Bei relativ schlanken Objekten hingegen ist das Flächenmodell erste Wahl; es erfordert auch weniger Modellierungs- und Berechnungsaufwand.
Plastische Materialeigenschaften wie beispielsweise das Fließverhalten lassen sich mithilfe des Zusatzmoduls RF-MAT NL abbilden. Hierbei sind auch benutzerdefinierte Spannungs-Dehnungs-Diagramme anhand empirisch ermittelter Daten möglich. Im vorgestellten Beispiel wurde das Standarddiagramm mit einem voreingestellten Verfestigungsfaktor verwendet.
Mithilfe nichtlinearer Materialmodelle können auch Umlagerungseffekte im Modell erfasst werden, die sich beispielsweise durch die Ausbildung plastischer Gelenke ergeben. Bei plastischen Effekten sind Ergebnisse mit großen Verformungen - insbesondere nach Theorie III. Ordnung - mit Vorsicht zu bewerten.
Weitere Erläuterungen und Beispiele finden sich in der Knowledge Base und den FAQs, die über die unten angegebenen Links aufrufbar sind.