Lageänderungen des Tragwerks werden an Knoten, Linien, Stäben, Flächen und Volumen des Modells ausgegeben; wählen Sie die entsprechende Unterkategorie in den Tabellen aus:
- 'Ergebnisse knotenweise'
- 'Ergebnisse linienweise'
- 'Ergebnisse stabweise'
- 'Ergebnisse flächenweise'
- 'Ergebnisse volumenweise'
Gruppierung der Ergebnisse
Die Ergebnisse von Eigenwertanalysen – das heißt die Ergebnisse linearer Stabilitätsanalysen – werden nach den Basisobjekten des Modells und der Eigenform gruppiert; wählen Sie den passenden Tab (Tabellenblatt) in den Tabellen aus:
- Knoten- / Linien- / Stab- / Flächen- / Volumen-Nummer oder
- Nummer der Eigenform
Bildstrecke Gruppierung von Ergebnissen:
Koordinaten von Ergebnispunkten
- Ergebnisse an Flächen und Volumen orientieren an den Rasterpunkten der Objekte und beziehen sich – genau wie Knotenergebnisse – auf das globale Koordinatensystem. Mehr Informationen dazu finden Sie im RFEM Handbuch.
- Ergebnisse an Stäben und Linien werden an speziellen Punkten ('Stelle x') entlang der Objekte im lokalen Koordinatensystem ausgegeben.
- Bei Selektion eines Rasterpunktes oder einer 'Stelle x' in den Tabellen wird die entsprechende Position am Modell markiert.
Normierte und absolute Ergebnisse
Verschiebungen und Verdrehungen aus Eigenwertanalysen – das heißt aus linearen Stabilitätsanalysen – werden als dimensionslose Zahlenwerte ausgegeben. Für die Normierung / Skalierung der Ergebnisse auf die Bezugslänge "1" wird eine der folgenden Basen genutzt:
| |u|= 1 | maximale Gesamtverschiebung |u|= (uX2 + uY2 + uZ2)0,5 |
| max {uX; uY; uZ} = 1 | maximaler Translationsanteil des Eigenformvektors; es werden nur Verschiebungen berücksichtigt |
| max {uX; uY; uZ; φX; φY; φZ} = 1 | maximaler Translations- oder Rotationsanteil des Eigenformvektors; es werden Verschiebungen und Verdrehungen berücksichtigt |
| {uj}T [KG] {uj} = 1 | maximaler Verformungswert aus der geometrischen Steifigkeitsmatrix |
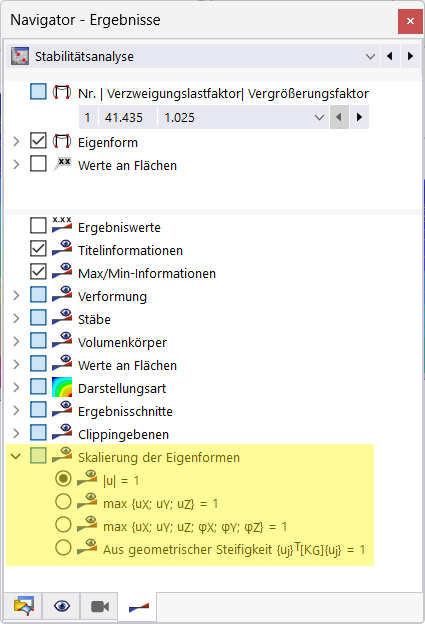
Die Basis der Normierung können Sie im Ergebnis-Navigator unter 'Skalierung der Eigenformen' einstellen.
Bild Skalierung der Eigenform:
Verschiebungen und Verdrehungen aus nichtlinearen, inkrementellen Berechnungen werden in absoluten Zahlenwerten angegeben.