Widerstandsmomente um Achsen y, z

Neu

27. Juli 2023

005400

Wie werden in RSECTION 1, DUENQ und DICKQ die Widerstandsmomente um die Achsen y, z berechnet?

Antwort

In DUENQ und DICKQ werden die Widerstandsmomente nach folgenden Formeln berechnet:

Minimales Widerstandsmoment um Achse y

$W_{y, m i n} = \frac{I_{y}}{e_{z, m i n}}$

I_y	Flächenträgheitsmoment um y-Achse
e_z,min	Größter Randabstand in negative Richtung der Schwerpunktachse z

Maximales Widerstandsmoment um Achse y

$W_{y, m a x} = \frac{I_{y}}{e_{z, m a x}}$

I_y	Flächenträgheitsmoment um y-Achse
e_z,max	Größter Randabstand in positive Richtung der Schwerpunktachse z

Minimales Widerstandsmoment um Achse z

$W_{z, m i n} = \frac{I_{z}}{e_{y, m i n}}$

I_z	Flächenträgheitsmoment um z-Achse
e_y,min	Größter Randabstand in negative Richtung der Schwerpunktachse y

Maximales Widerstandsmoment um Achse z

$W_{z, m a x} = \frac{I_{z}}{e_{y, m a x}}$

I_z	Flächenträgheitsmoment um z-Achse
e_y,max	Größter Randabstand in positive Richtung der Schwerpunktachse y

Mit den so berechneten Widerstandsmomenten können Sie für unsymmetrische Querschnitte nicht direkt die extreme Normalspannung aus dem Biegemoment M_y bzw. M_z berechnen.

In RSECTION werden die Widerstandsmomente so bestimmt, dass sie die direkte Berechnung extremer Normalspannungen aus den Biegemomenten M_y bzw. M_z ermöglichen.

Das Widerstandsmoment um die Achse y am Punkt i der Außenkontur des Querschnitts bestimmen Sie wie folgt:

Widerstandsmoment am Punkt i um Achse y

$W_{y, i} = \frac{I_{y} \cdot I_{z} - {I_{y z}}^{2}}{I_{z} \cdot z_{i} - I_{y z} \cdot y_{i}}$

I_y	Flächenträgheitsmoment um y-Achse
I_z	Flächenträgheitsmoment um z-Achse
I_yz	Zentrifugalmoment um y, z- Achsen
y_i	y-Koordinate des Punkt i im Achsensystem y,z
z_i	z-Koordinate des Punkt i im Achsensystem y,z

Das Widerstandsmoment um die Achse z am Punkt i der Außenkontur des Querschnitts wird wie folgt bestimmt:

Widerstandsmoment am Punkt i um Achse z

$W_{z, i} = \frac{I_{y} \cdot I_{z} - {I_{y z}}^{2}}{I_{y} \cdot y_{i} - I_{y z} \cdot z_{i}}$

I_y	Flächenträgheitsmoment um y-Achse
I_z	Flächenträgheitsmoment um z-Achse
I_yz	Zentrifugalmoment um y, z- Achsen
y_i	y-Koordinate des Punkt i im Achsensystem y,z
z_i	z-Koordinate des Punkt i im Achsensystem y,z

Das minimale Widerstandmoment um die Achse y bzw. z ist das größte negative Widerstandsmoment der Punkte i. Das maximale Widerstandmoment um die Achse y bzw. z ist das kleinste positive Widerstandsmoment der Punkte i. Die maßgebenden Widerstandsmomente um die Achse y bzw. z werden wie folgt berechnet:

Widerstandsmoment um Achse y

$W_{y} = m i n (|W_{y, m i n}|, |W_{y, m a x}|)$

W_y,min	Größtes negatives Widerstandsmoment um Achse y
W_y,max	Kleinstes positives Widerstandsmoment um Achse y

Widerstandsmoment um Achse z

$W_{z} = m i n (|W_{z, m i n}|, |W_{z, m a x}|)$

W_z,min	Größtes negatives Widerstandsmoment um Achse z
W_z,max	Kleinstes positives Widerstandsmoment um Achse z

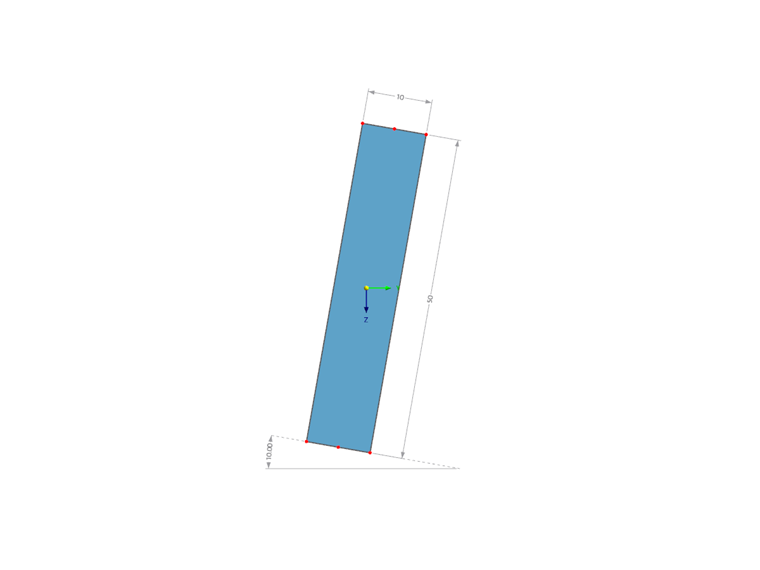
Im Bild 1 ist ein um 10° geneigter Rechteckquerschnitt mit den Abmessungen b/h = 50/10 mm dargestellt.

Rechteckquerschnitt b/h = 50/10 mm um 10° geneigt

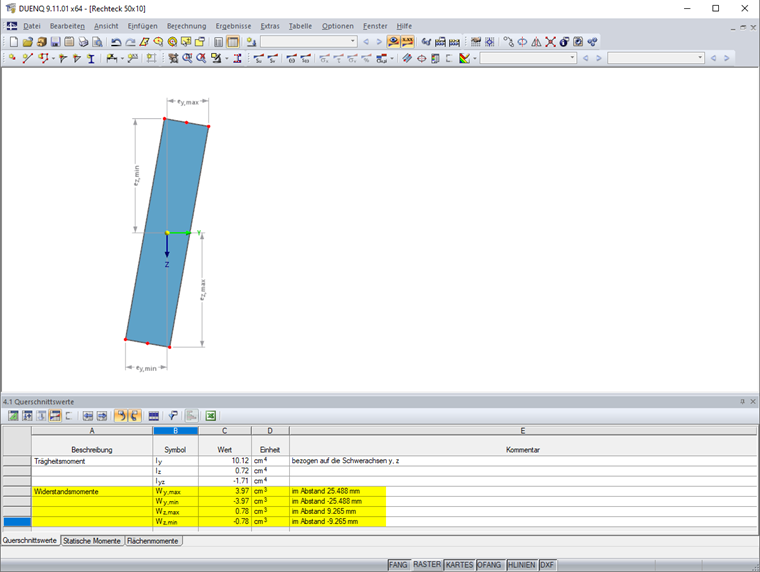
In DUENQ bzw. DICKQ ergeben sich die folgenden Widerstandsmomente W_y,min, W_y,max, W_z,min und W_z,max (Bild 2):

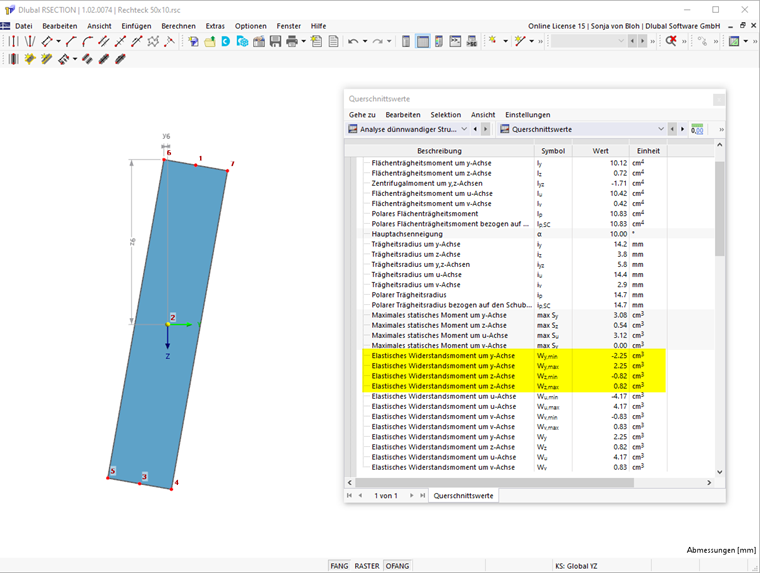
Widerstandsmomente um Achsen y, z

Minimales Widerstandsmoment um Achse y

$W_{y, m i n} = \frac{I_{y}}{e_{z, m i n}} = \frac{10, 12}{- 2, 5488} = - 3, 97 c m^{3}$

Maximales Widerstandsmoment um Achse y

$W_{y, m a x} = \frac{I_{y}}{e_{z, m a x}} = \frac{10, 12}{2, 5488} = 3, 97 c m^{3}$

Minimales Widerstandsmoment um Achse z

$W_{z, m i n} = \frac{I_{z}}{e_{y, m i n}} = \frac{0, 72}{- 0, 9265} = - 0, 78 c m^{3}$

Maximales Widerstandsmoment um Achse z

$W_{z, m a x} = \frac{I_{z}}{e_{y, m a x}} = \frac{0, 72}{0, 9265} = 0, 78 c m^{3}$

In RSECTION ergeben sich die folgenden Widerstandsmomente W_y,min, W_y,max, W_z,min und W_z,max (Bild 3):

Widerstandsmomente um Achsen y, z

Minimales Widerstandsmoment um Achse y (Punkt 6)

$W_{y, m i n} = \frac{I_{y} \cdot I_{z} - {I_{y z}}^{2}}{I_{z} \cdot z_{6} - I_{y z} \cdot y_{6}} = \frac{10, 12 \cdot 0, 72 - {(- 1, 71)}^{2}}{0, 72 \cdot (- 2, 549) - (- 1, 71) \cdot (- 0, 058)} = - 2, 25 c m^{3}$

Maximales Widerstandsmoment um Achse y (Punkt 4)

$W_{y, m a x} = \frac{I_{y} \cdot I_{z} - {I_{y z}}^{2}}{I_{z} \cdot z_{4} - I_{y z} \cdot y_{4}} = \frac{10, 12 \cdot 0, 72 - {(- 1, 71)}^{2}}{0, 72 \cdot 2, 549 - (- 1, 71) \cdot 0, 058} = 2, 25 c m^{3}$

Minimales Widerstandsmoment um Achse z (Punkt 5)

$W_{z, m i n} = \frac{I_{y} \cdot I_{z} - {I_{y z}}^{2}}{I_{y} \cdot y_{5} - I_{y z} \cdot z_{5}} = \frac{10, 12 \cdot 0, 72 - {(- 1, 71)}^{2}}{10, 12 \cdot (- 0, 927) - (- 1, 71) \cdot 2, 375} = - 0, 82 c m^{3}$

Maximales Widerstandsmoment um Achse z (Punkt 7)

$W_{z, m i n} = \frac{I_{y} \cdot I_{z} - {I_{y z}}^{2}}{I_{y} \cdot y_{7} - I_{y z} \cdot z_{7}} = \frac{10, 12 \cdot 0, 72 - {(- 1, 71)}^{2}}{10, 12 \cdot 0, 927 - (- 1, 71) \cdot (- 2, 375)} = 0, 82 c m^{3}$

Schlüsselwörter

Widerstandsmoment

Downloads

Schreiben Sie einen Kommentar...

0 Kommentieren

0 0

Gehe zu
Events
Videos
Modelle
Knowledge Base
Screenshots
Produkt-Features
Häufig gestellte Fragen
Kundenprojekte

Empfohlene Veranstaltungen

Bemessung von massiven RSECTION-Querschnitten in RFEM 6

Webinar 14. September 2023 14:00 - 15:00 CEST

Bemessung von massiven RSECTION-Querschnitten in RFEM 6

Webinar 12. September 2023 14:00 - 15:00 CEST

Bemessung kaltgeformter Stahlprofile nach AISI S100/CSA S136 in RFEM 6 (USA)

Webinar 21. Juni 2023 14:00 - 15:00 EDT

RSECTION | Studenten | Einführung in die Festigkeitslehre

Online-Schulung 24. April 2023 16:00 - 17:00 CEST

Modellierung und Bemessung kaltgeformter Stahlprofile nach EC 3 in RFEM 6

Webinar 20. April 2023 14:00 - 15:00 CEST

Modellierung und Bemessung kaltgeformter Stahlprofile nach EC 3 in RFEM 6

Webinar 18. April 2023 14:00 - 15:00 CEST

Modellierung von Querschnitten in RSECTION 1

Webinar 30. März 2023 14:00 - 15:00 CEST

Modellierung von Querschnitten in RSECTION 1

Webinar 28. März 2023 14:00 - 15:00 CEST

RSECTION | Studenten | Einführung in die Festigkeitslehre

Online-Schulung 18. Oktober 2022 16:00 - 17:30 CEST

Ermittlung der Querschnittswerte und Spannungsanalyse in RSECTION 1

Ermittlung von Querschnittswerten und Spannungsanalyse in RSECTION 1

Webinar 18. August 2022 14:00 - 15:00 CEST

Ermittlung von Querschnittswerten in RSECTION 1

Ermittlung von Querschnittswerten und Spannungsanalyse in RSECTION 1

Webinar 16. August 2022 14:00 - 15:00 CEST

$Aluminiumbemessung nach ADM 2020 \n in RFEM 6$

Aluminiumbemessung nach ADM 2020 in RFEM 6 (USA)

Webinar 25. Mai 2022 14:00 - 15:00 EDT

Weitere Veranstaltungen

Videos

Webinar | Bemessung von massiven RSECTION-Querschnitten in RFEM 6

Länge min

Bemessung von massiven RSECTION-Querschnitten in RFEM 6

Länge 45:04 min

KB 001826 | Erstellung von Querschnitten mittels DXF-Vorlage

Länge 2:16 min

WIN | 08/2023 - Was ist neu in RFEM 6 und RSTAB 9?

Länge 2:15 min

Bemessung kaltgeformter Stahlprofile nach AISI S100/CSA S136 in RFEM 6 (USA)

Länge 1:03:17 min

RFEM 6 für Studenten | Einführung in die Festigkeitslehre | 18.04.2023

Länge 1:17:15 min

Modellierung von Querschnitten in RSECTION 1

Länge 52:55 min

WIN | 02/2023 - Was ist neu in RFEM 6 und RSTAB 9?

Länge 1:56 min

WIN | 01/2023 - Was ist neu in RFEM 6 und RSTAB 9?

Länge 1:36 min

Weitere Videos

Modelle zum Herunterladen

Beiträge aus der Knowledge Base

Neu

Erstellung von Querschnitten mittels DXF-Vorlage

In diesem Beitrag wird Ihnen die Erstellung von Querschnitten mithilfe von DXF-Dateien gezeigt.

Nutzung der WebService API in Verbindung mit EXCEL und Python Analyse dünnwandiger Strukturen in RSECTION 1 Ermittlung der Querschnittswerte und Spannungsnachweis in RSECTION 1 Statik, die Spaß macht…

Weitere Beiträge aus der Knowledge Base

Screenshots

Beiträge zu Produkt-Features

Neu

Bemessung von RSECTION-Querschnitten im Add-On Betonbemessung

RSECTION-Querschnitt aus DXF-Datei erzeugen Eigenform für Forminstabilität Speichern als Version Intuitiver Aufruf der Handbuchkapitel

Weitere Produkt-Features

Häufig gestellte Fragen (FAQs)

Weitere häufig gestellte Fragen

Kundenprojekte

Fußgängerbrücke Freischütz

Isarsteg Nord bei Freising

Hervester Brücke Nr. 423 über den Wesel-Datteln-Kanal

Neubau der Güsener Straßenbrücke B 10 über den Elbe-Havel-Kanal

Baku Flame Towers, Aserbaidschan

Neubau einer Tiefbohranlage

Oberwagen Schiffsbelader

Brücke über Schleifenwagen für Förderbandanlage in Usbekistan

Bandbrücke für Förderbandanlage in Usbekistan

Weitere Kundenprojekte

Widerstandsmomente um Achsen y, z

Fragen & Antworten, die Ihnen weiterhelfen

Wie werden in RSECTION 1, DUENQ und DICKQ die Widerstandsmomente um die Achsen y, z berechnet?

Antwort

Schlüsselwörter

Downloads