Retour aux manuels en ligne

2365x

000483

Dipl.-Ing. (FH) Robert Vogl

27.04.2023

Sélectionner le Manuel

Aperçu

Interface graphique utilisateur et paramètres

Dlubal Center

Modèle - Données de base

Structure

Imperfections

Cas de charge et combinaisons

Assistants de charge

Charges

Objets de résultats

Calcul

Résultats

Objets repère

Fonctionnalités du programme

Évaluation des résultats

Rapport d’impression

Résultats par solide

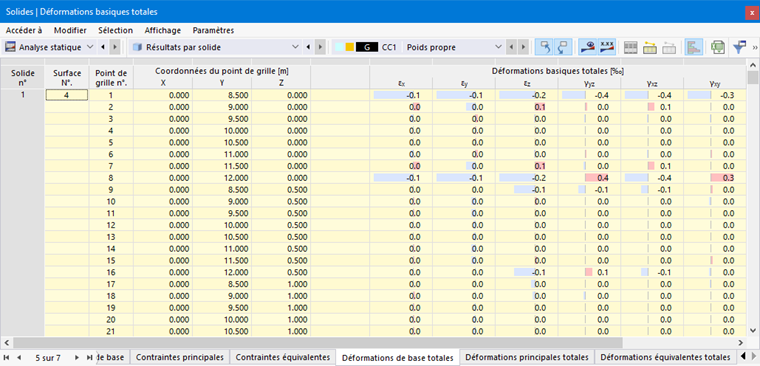
Vous pouvez afficher les résultats pour le volume graphiquement via la catégorie du navigateur Corps volumétriques. Les résultats numériques des volumes se trouvent dans la catégorie de tableaux Résultats par volume.

Résultats par solide dans le tableau

Informations

Dans le tableau et dans le graphique, les résultats présents sur les surfaces limites du corps volumétrique sont affichés. Pour vérifier les résultats à l'intérieur du corps volumétrique, activez dans la catégorie inférieure Valeurs sur surfaces l'option Sur les points de maillage FE. Les valeurs à l'intérieur du corps volumétrique peuvent ensuite être lues via un plan de coupe (voir chapitre Plans de coupe).

Déformations

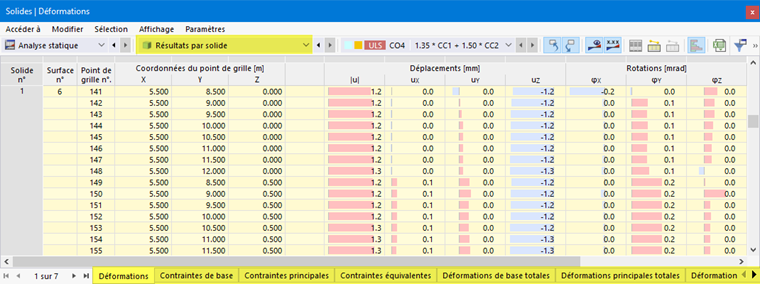
L'image Résultats par volume dans tableau montre le tableau avec les déformations des surfaces limites. Les déplacements et les rotations sont affichés dans les points de grille des surfaces (voir chapitre Surfaces ).

Astuce

Pour les petites surfaces, la maille de grille standard de 0.5 m peut entraîner l'existence de peu de points de grille. Adaptez dans ce cas le nombre ou l'espacement des points de grille à la taille de la surface.

Les déformations signifient :

\|u\|	Valeur absolue du déplacement total
u_X	Déplacement dans la direction de l'axe global X
u_Y	Déplacement dans la direction de l'axe global Y
u_Z	Déplacement dans la direction de l'axe global Z
φ_X	Rotation autour de l'axe global X
φ_Y	Rotation autour de l'axe global Y
φ_Z	Rotation autour de l'axe global Z

Contraintes

Sélectionner les contraintes dans les solides dans le navigateur

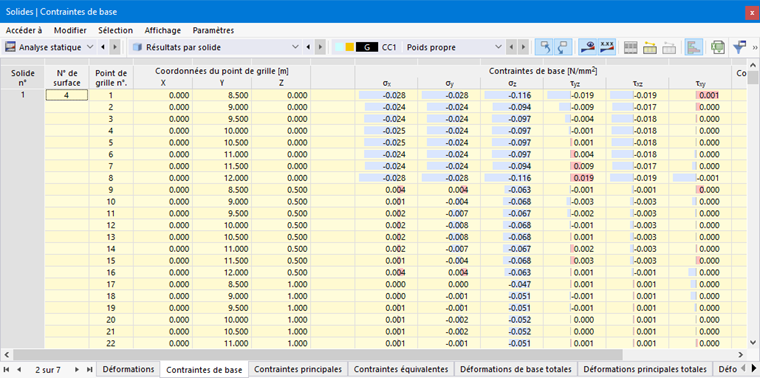
Contraintes des solides dans le tableau

Définissez dans le navigateur quelles contraintes doivent être affichées sur les surfaces limites des volumes. Le tableau répertorie les contraintes de ces surfaces selon les spécifications définies dans le Gestionnaire de tableaux de résultats .

Les contraintes volumétriques sont divisées en catégories suivantes :

Contraintes de base
Contraintes principales
Contraintes équivalentes
Invariants de contrainte

Les contraintes volumétriques ne peuvent pas être décrites comme les contraintes surfaciques avec des équations simples. Les contraintes de base σ_x, σ_y et σ_z y compris les contraintes de cisaillement τ_yz, τ_xz et τ_xy sont directement déterminées par le noyau de calcul.

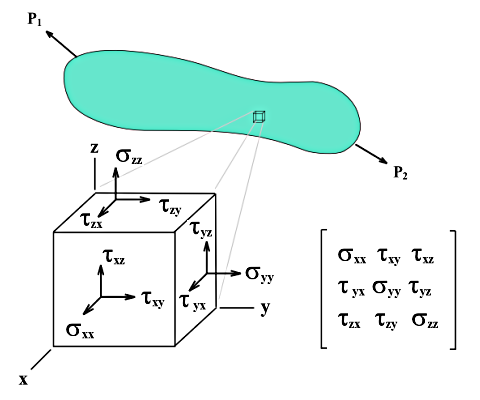
Si un cube de dimensions d_x, d_y et d_z est coupé dans un corps soumis à des contraintes multiaxiales, les contraintes sur chaque face du cube peuvent être décomposées en contraintes normales et de cisaillement. En négligeant la force volumique et également les différences de contrainte sur les faces parallèles, l'état de contrainte dans le système de coordonnées local du cube peut être décrit par neuf composants de contrainte.

Volumenelement mit Spannungskomponenten

La matrice du tenseur de contrainte est donnée par :

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Matrice du tenseur des contraintes

Les valeurs propres du tenseur donnent les contraintes principales σ₁, σ₂ et σ_{3> comme suit :}

\det (S - σ E) = 0

E	3x3 Einheitsmatrix

Contraintes principales

La '''contrainte de cisaillement''' maximale τ_max est déterminée selon le cercle de contrainte de Mohr :

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Contrainte maximale de cisaillement

Astuce

Avec l'entrée du navigateur '''σ₁₂₃''', vous pouvez afficher graphiquement les trajectoires des contraintes principales.

Les '''contraintes équivalentes''' σ_v selon von Mises peuvent être déterminées par deux formules équivalentes.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Contrainte équivalente σ_{v, Mises} à partir des contraintes principales

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Contrainte équivalente σ_v,Mises à partir des contraintes de base

Pour la détermination de la contrainte équivalente σ_v selon Tresca , les différences des contraintes principales sont examinées afin de déterminer la valeur maximale.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Contrainte équivalente σ_v,Tresca

La contrainte équivalente σ_v selon Rankine est déterminée à partir des valeurs absolues maximales des contraintes principales.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Contrainte équivalente_{v, Rankine}

Pour déterminer la contrainte équivalente σ_v selon Bach , les différences de contrainte principales sont examinées, en tenant compte du coefficient de Poisson ν, afin de déterminer la valeur maximale.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Contrainte équivalente_{v, Bach}

Les '''invariants de contrainte''' permettent une évaluation ciblée de l'état de contrainte. À partir des contraintes principales, la contrainte moyenne p est déterminée :

p = \frac{σ_{1} + σ_{2} + σ_{3}}{3} = \frac{I_{1}}{3}

σ₁ , σ₂ , σ₃	Contraintes principales
I₁	Premier invariant des contraintes

Pression moyenne p

La contrainte déviatorique q est déterminée comme suit :

q = \sqrt{{σ_{1}}^{2} + {σ_{2}}^{2} + {σ_{3}}^{2} - σ_{1} σ_{2} - σ_{2} σ_{3} - σ_{3} σ_{1}}

= \frac{1}{\sqrt{2}} \sqrt{{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}} = \sqrt{{I_{1}}^{2} - 3 I_{2}} = \sqrt{3 J_{2}}

I₁	Première Invariante de contrainte
I₂	Deuxième invariant de contrainte
J₂	Deuxième invariant de contrainte déviatoire

Contrainte déviatorique q

L'angle de Lode θ peut être considéré comme une mesure du type de chargement. Il se situe entre -30° et +30° et est déterminé comme suit :

θ = \frac{1}{3} \sin^{- 1} (- \frac{3 \sqrt{3}}{2} \frac{J_{3}}{{J_{2}}^{3 / 2}})

J₂	Deuxième invariant de contrainte de déviation : 1/6 [(σ₁ – σ₂)² + (σ₂ – σ₃)² + (σ₃ – σ₂)²]
J₃	Troisième invariant des contraintes déviatoires : 1/27 (2σ₁ – σ₂ – σ₃) (2σ₂ – σ₃ – σ₁) (2σ₃ – σ₁ – σ₂)

Angle de Lode θ

== Déformations ==

Sélection des distorsions de volume dans le Navigateur

Sélectionner « Distorsions de solide » dans le Navigateur

Déformations de solides dans le tableau

Définissez dans le navigateur quelles déformations doivent être affichées sur les surfaces limites des volumes. Le tableau répertorie les déformations de ces surfaces selon les spécifications définies dans le Gestionnaire de tableaux de résultats . Les déformations volumétriques sont divisées en catégories suivantes : * Déformations totales de base * Déformations principales totales * Déformations totales équivalentes * Invariants de déformation Les '''déformations totales de base''' y compris les déformations de cisaillement sont directement déterminées par le noyau de calcul. Pour l'état de déformation spatial, la définition générale du tenseur est la suivante :

ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]

Tenseur pour l'état de déformation

Les éléments du tenseur sont définis comme suit :

ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})

Éléments tenseurs

À partir des déformations de base, les '''déformations principales totales''' ε₁, ε₂ et ε₃ sont déterminées.

Astuce

Avec l'entrée du navigateur '''ε₁₂₃''', vous pouvez afficher graphiquement les trajectoires des déformations principales.

Les '''déformations totales équivalentes''' ε_v sont déterminées comme suit selon quatre hypothèses de contrainte différentes.

ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}

Déformation totale comparative ε_v,Mises

ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)

R	Matrice (voir ci-dessous)

Déformation totale comparative ε_v,Tresca (Différences de valeurs propres maximales selon la matrice R)

ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)

R	Matrix (siehe unten)

Vergleichsgesamtdehnung ε_v,Rankine (Maximum der Eigenwerte gemäß Matrix R)

ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)

R	Matrice (voir ci-dessous)

Déformation totale comparative ε_v,Bach (Différences de valeurs propres maximales selon la matrice R avec prise en compte du coefficient de Poisson ν)

R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]

Matrice R

Les '''invariants de déformation''' permettent une évaluation ciblée de l'état de déformation. À partir des déformations principales, l'invariant de déformation volumétrique ε_v est déterminé :

ε_{v} = ε_{11} + ε_{22} + ε_{33}

Invariante de déformation volumétrique ε_v

Les déformations de cisaillement ε_q sont déterminées comme suit :

ε_{q} = \frac{1}{3} \sqrt{2 [{(ε_{11} - ε_{22})}^{2} + {(ε_{22} - ε_{33})}^{2} + {(ε_{33} - ε_{11})}^{2}] + 3 (2 {ε_{12}}^{2} + 2 {ε_{23}}^{2} + 2 {ε_{31}}^{2})}

Déformation de cisaillement ε_q

Chapitre parent

Résultats