Zpět k online manuálům

2360x

000483

Dipl.-Ing. (FH) Robert Vogl

27.4.2023

Vybrat manuál

Přehled

Uživatelské prostředí a nastavení

Dlubal centrum

Základní údaje o modelu

Konstrukce

Imperfekce

Zatěžovací stavy a kombinace

Generátor zatížení

Zatížení

Výsledkové objekty

Výpočet

Výsledky

Pomocné objekty

Funkce programu

Vyhodnocení výsledků

Tiskové protokoly

Výsledky po objemech

Výsledky pro objemy můžete zobrazit graficky v navigátoru v kategorii Tělesa. Numerické objemové výsledky naleznete v kategorii tabulek Výsledky podle objemů.

Výsledky podle těles v tabulce

Informace

V tabulce a v grafice jsou zobrazeny výsledky platné na ohraničujících plochách objemového tělesa. Pro kontrolu výsledků uvnitř objemu aktivujte v dolní části kategorie Hodnoty na plochách možnost Na FE síťových bodech. Hodnoty v objemovém tělese můžete následně odečíst pomocí ořezové roviny (viz kapitola Ořezové roviny).

Deformace

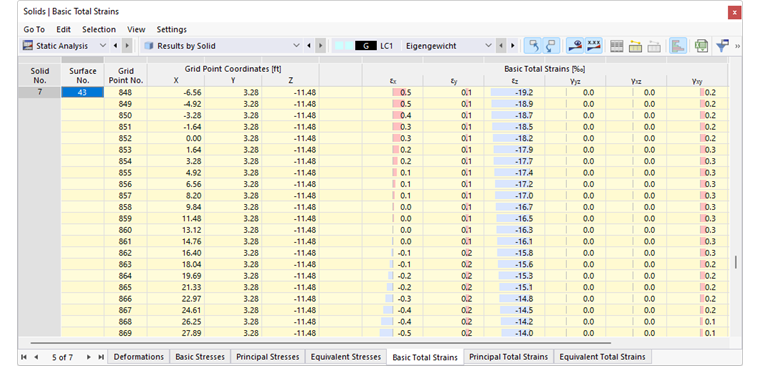
Obrázek Výsledky podle objemů v tabulce ukazuje tabulku s deformacemi ohraničujících ploch. Posuny a natočení jsou vypsány v síťových bodech ploch (viz kapitola Plochy ).

Tip

Při malých plochách může standardní síť s velikostí oka 0,5 m vést k tomu, že existuje jen několik síťových bodů. Přizpůsobte v takovém případě počet nebo vzdálenost síťových bodů velikosti plochy.

Deformace znamenají:

\|u\|	Absolutní hodnota celkového posunu
u_X	Posun ve směru globální osy X
u_Y	Posun ve směru globální osy Y
u_Z	Posun ve směru globální osy Z
φ_X	Natočení kolem globální osy X
φ_Y	Natočení kolem globální osy Y
φ_Z	Natočení kolem globální osy Z

Napětí

Výběr hlavních napětí v pevných látkách v navigátoru

Napětí těles v tabulce

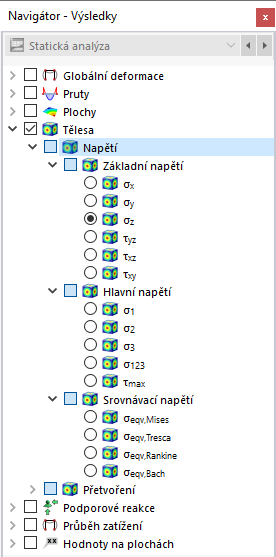
V navigátoru určete, která napětí na ohraničujících plochách objemů mají být zobrazena. Tabulka obsahuje napětí těchto ploch podle specifikací nastavených v Správce výsledkových tabulek .

Objemová napětí jsou rozdělena do následujících kategorií:

Základní napětí
Hlavní napětí
Ekvivalentní napětí
Invarianty napětí

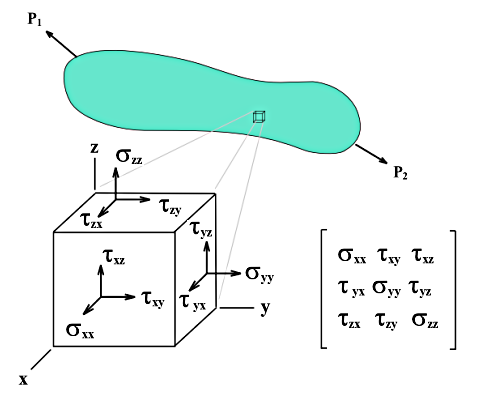
Objemová napětí nelze popsat jednoduchými rovnicemi jako napětí na plochách. Základní napětí σ_x, σ_y a σ_z včetně smykových napětí τ_yz, τ_xz a τ_xy jsou přímo vypočítána výpočetním jádrem.

Odřízneme-li krychli s délkami hran d_x, d_y a d_z z tělesa namáhaného více osově, můžeme napětí v každé ploše krychle rozdělit na normální a smyková napětí. Při zanedbání objemové síly a rozdílů napětí na rovnoběžných plochách lze v lokálním souřadném systému krychle popsat stav napětí devíti komponentami napětí.

Volumenelement mit Spannungskomponenten

Matici napěťového tenzoru tvoří:

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Matice tenzoru napětí

Z vlastní hodnot tenzoru se hlavní napětí σ₁, σ₂ a σ₃ určí následujícím způsobem:

\det (S - σ E) = 0

E	3x3 Einheitsmatrix

Hlavní napětí

Maximální smykové napětí τ_max je určeno podle Mohrského kruhu napětí:

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Maximální smykové napětí

Tip

Pomocí navigačního záznamu σ₁₂₃ můžete graficky zobrazit trajektorie hlavních napětí.

Ekvivalentní napětí σ_v podle von Mises lze určit pomocí dvou rovnocenných vzorců.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Srovnávací napětí σ_{v, Mises} z hlavních napětí

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Srovnávací napětí σ_{v, Mises} ze základních napětí

Pro určení ekvivalentního napětí σ_v podle Tresca se zkoumají rozdíly hlavních napětí s cílem určit maximální hodnotu.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Srovnávací napětí σ_{v, Tresca}

Ekvivalentní napětí σ_v podle Rankine se určuje z největších absolutních hodnot hlavních napětí.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Srovnávací napětí σv_{, Rankine}

Pro určení ekvivalentního napětí σ_v podle Bach jsou zkoumány rozdíly hlavních napětí s přihlédnutím k Poissonově číslu ν, a určuje se z nich maximální hodnota.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Srovnávací napětí σ_{v, Bach}

Invarianty napětí umožňují cílené posouzení stavu napětí. Z hlavních napětí se určí střední napětí p:

p = \frac{σ_{1} + σ_{2} + σ_{3}}{3} = \frac{I_{1}}{3}

σ₁ , σ₂ , σ₃	Hlavní napětí
I₁	První invariant napětí

Střední napětí p

Deviatorické napětí q se vypočítá následujícím způsobem:

q = \sqrt{{σ_{1}}^{2} + {σ_{2}}^{2} + {σ_{3}}^{2} - σ_{1} σ_{2} - σ_{2} σ_{3} - σ_{3} σ_{1}}

= \frac{1}{\sqrt{2}} \sqrt{{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}} = \sqrt{{I_{1}}^{2} - 3 I_{2}} = \sqrt{3 J_{2}}

I₁	První invariant napětí
I₂	Druhý invariat napětí
J₂	Druhá deviátorická invariant napětí

Deviátorové napětí q

Lodeho úhel θ může být považován za měřítko druhu zatížení. Nachází se v rozmezí mezi -30° a +30° a je určen následovně:

θ = \frac{1}{3} \sin^{- 1} (- \frac{3 \sqrt{3}}{2} \frac{J_{3}}{{J_{2}}^{3 / 2}})

J₂	Druhá invariant deviátového napětí: 1/6 [(σ1 – σ2)^2 + (σ2 – σ3)^2 + (σ3 – σ1)^2]
J₃	Třetí deviátorický invariant napětí: 1/27 (2σ₁ – σ₂ – σ₃) (2σ₂ – σ₃ – σ₁) (2σ₃ – σ₁ – σ₂)

Natočení podpory θ

Deformace

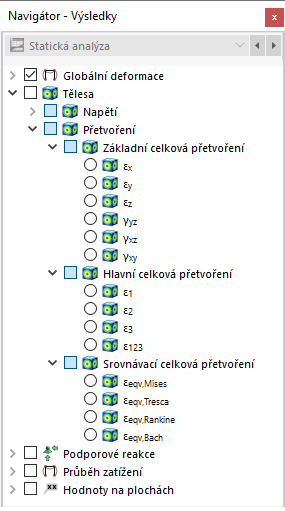
Výběr volumetrických deformací v navigátoru

Výběr deformací tělesa v navigátoru

Přetvoření na tělesech v tabulce

V navigátoru určete, které deformace na ohraničujících plochách objemů mají být zobrazeny. Tabulka obsahuje deformace těchto ploch podle specifikací nastavených v Správce výsledkových tabulek .

Objemové deformace jsou rozděleny do následujících kategorií:

Základní celkové deformace
Hlavní celkové deformace
Ekvivalentní celkové deformace
Invarianty deformací

Základní celkové deformace včetně smykových deformací jsou přímo vypočítány výpočetním jádrem. Pro prostorový stav deformace je obecná definice tenzoru: