Назад к руководствам онлайн

2375x

000483

Dipl.-Ing. (FH) Robert Vogl

2023-04-27

Выбрать руководство

Обзор

Графический интерфейс пользователя и настройки

Центр Dlubal

основные данные о модели

Конструкция

Несовершенства

Загружения и сочетания нагрузок

Мастера нагрузок

Нагрузки

Результирующие объекты

Вычисление

Результат

Вспомогательные объекты

Функции программы

Анализ результатов

Протокол результатов

Результаты по телам

Вы можете графически отобразить результаты для объемов в категории навигатора Объемные тела. Числовые результаты по объему найдены в категории таблиц Результаты по объему.

Результаты по телам в таблице

Инфо

В таблице и на графике отображаются результаты, имеющиеся на граничных поверхностях объемного тела. Чтобы проверить результаты внутри объемного тела, активируйте в нижней категории Значения на поверхностях опцию В узлах конечных элементов. Значения внутри объемного тела можно затем считать с помощью отсечной плоскости (см. главу Отсечные плоскости).

Деформации

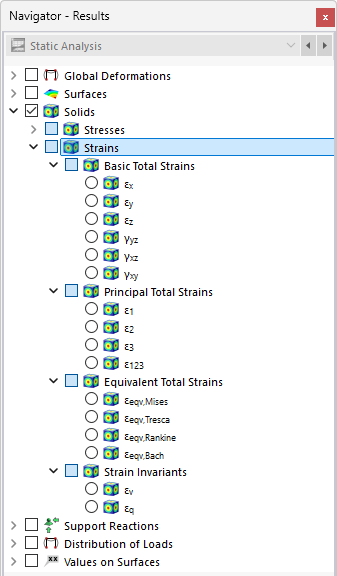
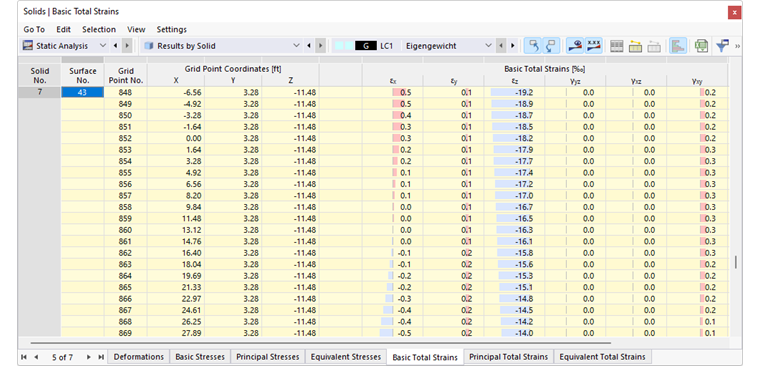
Изображение Результаты по объему в таблице показывает таблицу с деформациями граничных поверхностей. Смещения и вращения выводятся в узлах сетки на поверхности (см. главу Поверхности ).

Совет

Для небольших площадей стандартная сетка с шагом 0.5 м может привести к existованию только нескольких узлов сети. В этом случае настройте количество или расстояние между узлами сетки в соответствии с размером площади.

Деформации означают:

\|u\|	Абсолютное значение общего смещения
u_X	Смещение в направлении глобальной X-оси
u_Y	Смещение в направлении глобальной Y-оси
u_Z	Смещение в направлении глобальной Z-оси
φ_X	Вращение вокруг глобальной X-оси
φ_Y	Вращение вокруг глобальной Y-оси
φ_Z	Вращение вокруг глобальной Z-оси

Напряжения

Выбор напряжений тела в навигаторе

Напряжения тел в таблице

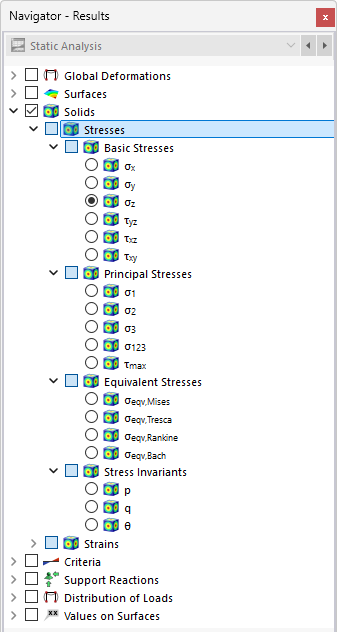
Определите в навигаторе, какие напряжения необходимо отображать на граничных поверхностях объемов. Таблица перечисляет напряжения этих поверхностей в соответствии с настройками, заданными в Менеджер таблиц результатов .

Объемные напряжения разделены на следующие категории:

Основные напряжения
Главные напряжения
Эквивалентные напряжения
Инварианты напряжений

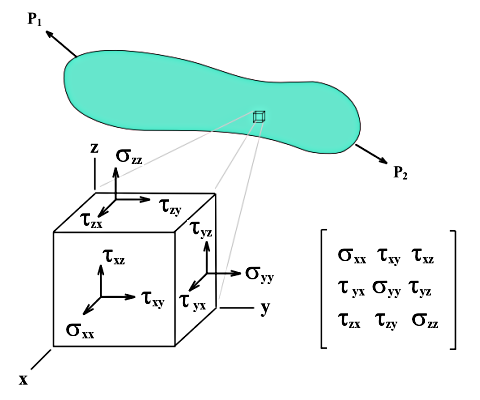
Объемные напряжения не могут быть описаны как поверхностные напряжения с помощью простых уравнений. Основные напряжения σ_x, σ_y и σ_z вместе с касательными напряжениями τ_yz, τ_xz и τ_xy напрямую определяются расчетным ядром.

Если от тела, подвергнутого многосекционному напряжению, отрезать куб с ребрами d_x, d_y и d_z, напряжения на каждой грани куба могут быть разложены на нормальные и касательные компоненты. Игнорируя объемные силы и различия напряжений на параллельных плоскостях, в локальной системе координат куба состояние напряжений может быть описано девятью компонентами напряжений.

Volumenelement mit Spannungskomponenten

Матрица тензора напряжений выглядит следующим образом:

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Матрица тензора напряжений

Собственные значения тензора определяются главные напряжения σ₁, σ₂ и σ_3>:

\det (S - σ E) = 0

E	3x3 Einheitsmatrix

Главные напряжения

Максимальное '''касательное напряжение''' τ_max определяется на основе круга напряжений Мора:

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Макс. касательные напряж.

Совет

С записом навигатора '''σ₁₂₃''' вы можете графически изобразить траектории главных напряжений.

'''Эквивалентные напряжения''' σ_v согласно методу Мизеса можно определить по двум равноценным формулам.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Эквивалентное напряжение σ_{v, Мизес} от главных напряжений

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Эквивалентное напряжение σ_{v, Мизес} от основных напряжений

Для определения эквивалентного напряжения σ_v по Треска изучаются разности главных напряжений, чтобы найти максимальное значение.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Эквивалентное напряжение σ_{v, Tresca}

Эквивалентное напряжение σ_v по Ранкину определяется из наибольших абсолютных значений главных напряжений.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Эквивалентное напряжение σ_{v, по Ранкина}

Для определения эквивалентного напряжения σ_v по Баху берутся к учету разницы главных напряжений с учетом коэффициента Пуассона ν, чтобы определить максимальное значение.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Эквивалентное напряжение σ_{v, Бах}

'''Инварианты напряжений''' позволяют целенаправленно оценить состояние напряжений. Из главных напряжений определяется среднее напряжение p:

p = \frac{σ_{1} + σ_{2} + σ_{3}}{3} = \frac{I_{1}}{3}

σ₁ , σ₂ , σ₃	Главные напряжения
I₁	Первый инвариант напряжений

Среднее напряжение p

Девиаторное напряжение q определяется следующим образом:

q = \sqrt{{σ_{1}}^{2} + {σ_{2}}^{2} + {σ_{3}}^{2} - σ_{1} σ_{2} - σ_{2} σ_{3} - σ_{3} σ_{1}}

= \frac{1}{\sqrt{2}} \sqrt{{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}} = \sqrt{{I_{1}}^{2} - 3 I_{2}} = \sqrt{3 J_{2}}

I₁	Первый инвариант напряжений
I₂	Второй инвариант напряжённоти
J₂	Второй инвариант девиаторных напряжений

Отклонённое напряжение q

Угол Лоде θ можно рассматривать как меру типа нагружения. Он находится в диапазоне от -30° до +30° и определяется следующим образом:

θ = \frac{1}{3} \sin^{- 1} (- \frac{3 \sqrt{3}}{2} \frac{J_{3}}{{J_{2}}^{3 / 2}})

J₂	Вторичный инвариант девиаторного напряжения: 1/6 [(σ1 – σ2)² + (σ2 – σ3)² + (σ3 – σ2)²]
J₃	Третья инварианта девиаторного напряжения: 1/27 (2σ₁ – σ₂ – σ₃) (2σ₂ – σ₃ – σ₁) (2σ₃ – σ₁ – σ₂)

Угол Лоде θ

== Деформации ==

Искажение объёмов в навигаторе

Деформации тел в таблице

Определите в навигаторе, какие деформации необходимо отображать на граничных поверхностях объемов. Таблица перечисляет деформации этих поверхностей в соответствии с настройками, заданными в Менеджер таблиц результатов . Объемные деформации разделены на следующие категории: * Основные суммарные деформации * Главные суммарные деформации * Эквивалентные суммарные деформации * Инварианты деформаций '''Основные суммарные деформации''', включая касательные деформации, напрямую определяются расчетным ядром. Для пространственного состояния деформации общее определение тензора выглядит следующим образом:

ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]

Тензор для деформированного состояния

Элементы тензора определяются следующим образом:

ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})

Тензорные элементы

Из основных деформаций определяются '''главные суммарные деформации''' ε₁, ε₂ и ε₃.

Совет

С записом навигатора '''ε₁₂₃''' вы можете графически изобразить траектории главных деформаций.

'''Эквивалентные суммарные деформации''' ε_v определяются по четырем различным гипотезам напряжения.

ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}

Сравнительная полная деформация ε_{v, по Мизесу}

ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)

R	Matrix (см.ниже)

Сравнительная общая деформация ε_v,Tresca (максимум разностей собственных значений по матрице R)

ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)

R	Matrix (siehe unten)

Vergleichsgesamtdehnung ε_v,Rankine (Maximum der Eigenwerte gemäß Matrix R)

ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)

R	Matrix (см.ниже)

Сравнительная полная деформация ε_{v, Бах} (максимум разности собственных чисел по матрице R с учетом коэффициента Пуассона ν)

R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]

Матрица R

'''Инварианты деформаций''' позволяют целенаправленно оценить состояние деформации. Из главных деформаций определяется объемное искажение ε_v:

ε_{v} = ε_{11} + ε_{22} + ε_{33}

Инвариант объёмного деформации ε_v

Касательные деформации ε_q определяются следующим образом:

ε_{q} = \frac{1}{3} \sqrt{2 [{(ε_{11} - ε_{22})}^{2} + {(ε_{22} - ε_{33})}^{2} + {(ε_{33} - ε_{11})}^{2}] + 3 (2 {ε_{12}}^{2} + 2 {ε_{23}}^{2} + 2 {ε_{31}}^{2})}

Сдвиговая деформация ε_q

Исходная глава

Результат