Torna a Manuali online

2361x

000483

Dipl.-Ing. (FH) Robert Vogl

2023-04-27

Seleziona il manuale

Panoramica

Interfaccia grafica utente e impostazioni

Dlubal Center

Dati di base del modello

Struttura

Imperfezioni

Casi e combinazioni di carico

Creazione guidata di carichi

Carichi

Oggetti risultanti

Calcolo

Risultati

Oggetti ausiliari

Strumenti

Valutazione dei risultati

Relazione di calcolo

Risultati per solido

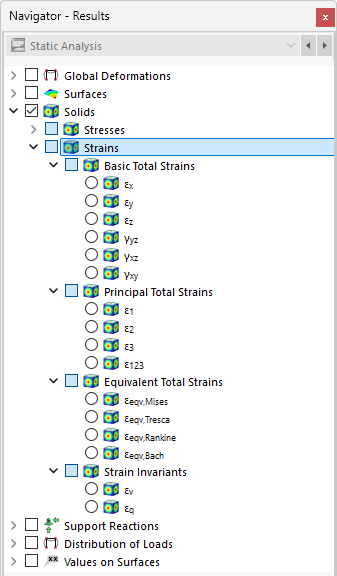
È possibile visualizzare i risultati per il volume graficamente attraverso la categoria del navigatore Volumenkörper. I risultati numerici del volume sono disponibili nella categoria tabella Ergebnisse volumenweise.

Risultati per solido nella tabella

Informazione

Nella tabella e nel grafico vengono visualizzati i risultati presenti sulle superfici di delimitazione del corpo volumetrico. Per verificare i risultati all'interno del corpo volumetrico, attivare nella categoria inferiore Valori sulle superfici l'opzione AI nodi di rete FE. I valori nel corpo volumetrico possono essere quindi letti tramite un piano di ritaglio (vedere capitolo Clippingebenen).

Deformazioni

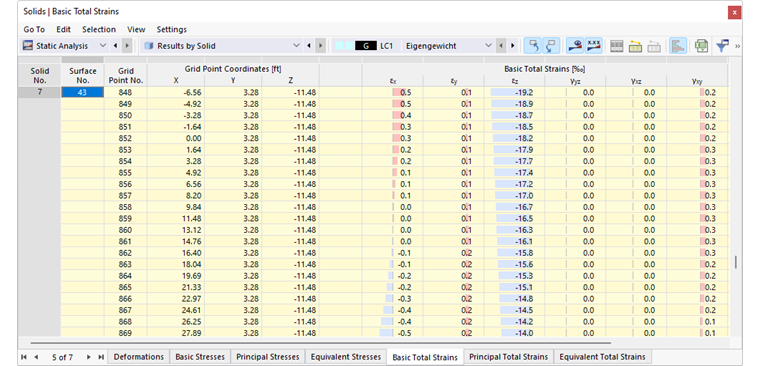
L'immagine Risultati volumenweise in tabella mostra la tabella con le deformazioni delle superfici di delimitazione. Gli spostamenti e le rotazioni vengono forniti nei punti di griglia delle superfici (vedi capitolo Flächen ).

Suggerimento

In caso di superfici piccole, la mesh standard della griglia di 0.5 m può comportare l'esistenza di pochi punti di griglia. In tal caso, adattare il numero o la distanza dei punti di griglia alla dimensione della superficie.

Le deformazioni significano:

\|u\|	Valore assoluto dello spostamento totale
u_X	Spostamento nella direzione dell'asse globale X
u_Y	Spostamento nella direzione dell'asse globale Y
u_Z	Spostamento nella direzione dell'asse globale Z
φ_X	Rotazione attorno all'asse globale X
φ_Y	Rotazione attorno all'asse globale Y
φ_Z	Rotazione attorno all'asse globale Z

Tensioni

Selezione delle tensioni solide nel Navigatore

Tensioni dei solidi nella tabella

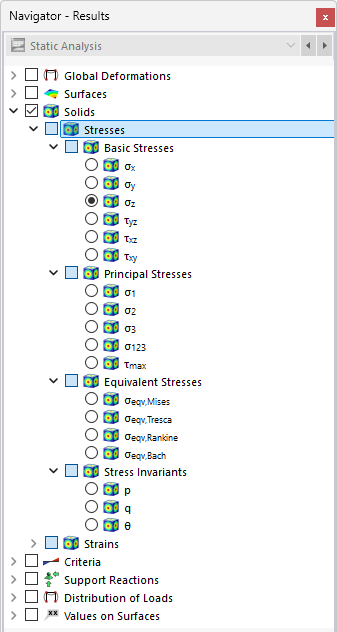
Nel navigatore, specificare quali tensioni devono essere visualizzate sulle superfici di delimitazione dei volumi. La tabella elenca le tensioni di queste superfici secondo le impostazioni specificate nel Manager delle tabelle dei risultati .

Le tensioni volumetriche sono suddivise nelle seguenti categorie:

Tensioni di base
Tensioni principali
Tensioni equivalenti
Invarianti di tensione

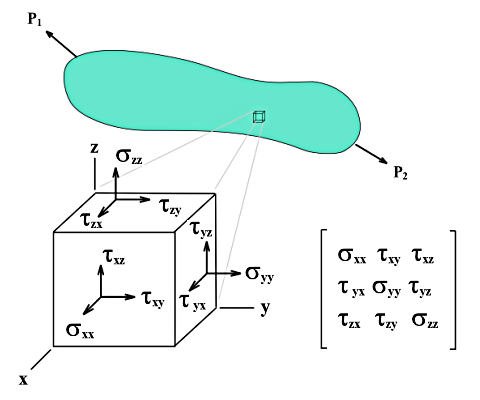
Le tensioni volumetriche non possono essere descritte con semplici equazioni come le tensioni sulle superfici. Le tensioni di base σ_x, σ_y e σ_z comprese le tensioni di taglio τ_yz, τ_xz e τ_xy vengono determinate direttamente dal nucleo di calcolo.

Quando viene tagliato un cubo con lunghezze laterali d_x, d_y e d_z da un corpo sottoposto a sforzo multiasse, le tensioni in ciascuna faccia del cubo possono essere decomposte in tensioni normali e di taglio. Trascurando la forza nello spazio e anche le differenze di tensione sulle superfici parallele, lo stato di tensione nel sistema di coordinate locale del cubo può essere descritto da nove componenti di tensione.

Volumenelement mit Spannungskomponenten

La matrice del tensore delle tensioni è la seguente:

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Matrice del tensore delle tensioni

Dai valori propri del tensore derivano le tensioni principali σ₁, σ₂ e σ_{3> nel modo seguente:}

\det (S - σ E) = 0

E	3x3 Einheitsmatrix

Tensioni principali

La '''tensione di taglio''' massima τ_max viene determinata secondo il cerchio di Mohr della tensione:

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Massima tensione tangenziale

Suggerimento

Con la voce del navigatore '''σ₁₂₃''' è possibile rappresentare graficamente le traiettorie delle tensioni principali.

Le '''tensioni equivalenti''' σ_v secondo von Mises possono essere determinate mediante due formule equivalenti.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Tensione equivalente σ_v,Mises dalle tensioni principali

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Tensione equivalente σ_v,Mises dalle tensioni di base

Per la determinazione della tensione equivalente σ_v secondo Tresca , vengono esaminati le differenze dalle tensioni principali per determinare il valore massimo.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Tensione equivalente_{v, Tresca}

La tensione equivalente σ_v secondo Rankine viene calcolata dai maggiori valori assoluti delle tensioni principali.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Tensione equivalente_{v, Rankine}

Per la determinazione della tensione equivalente σ_v secondo Bach , vengono esaminati le differenze delle tensioni principali considerando il coefficiente di Poisson ν per determinare il valore massimo.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Tensione equivalente_{v, Bach}

Le '''invarianti di tensione''' consentono una valutazione mirata dello stato di tensione. Dalle tensioni principali viene determinata la tensione media p:

p = \frac{σ_{1} + σ_{2} + σ_{3}}{3} = \frac{I_{1}}{3}

σ₁ , σ₂ , σ₃	Tensioni principali
I₁	Prima invariante di tensione

Pressione media p

La tensione deviatorica q viene calcolata come segue:

q = \sqrt{{σ_{1}}^{2} + {σ_{2}}^{2} + {σ_{3}}^{2} - σ_{1} σ_{2} - σ_{2} σ_{3} - σ_{3} σ_{1}}

= \frac{1}{\sqrt{2}} \sqrt{{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}} = \sqrt{{I_{1}}^{2} - 3 I_{2}} = \sqrt{3 J_{2}}

I₁	Primo invariante di tensione
I₂	Seconda invariante di tensione
J₂	Seconda invariante di tensione deviatric

Sforzo deviatorico q

L'angolo di Lode θ può essere considerato una misura del tipo di carico. Si trova nell'intervallo tra -30° e +30° e viene determinato come segue:

θ = \frac{1}{3} \sin^{- 1} (- \frac{3 \sqrt{3}}{2} \frac{J_{3}}{{J_{2}}^{3 / 2}})

J₂	Seconda invariante delle tensioni deviatoriche: 1/6 [(σ₁ – σ₂)² + (σ₂ – σ₃)² + (σ₃ – σ₂)²]
J₃	Invariante di tensione deviatorica del terzo ordine: 1/27 (2σ₁ – σ₂ – σ₃) (2σ₂ – σ₃ – σ₁) (2σ₃ – σ₁ – σ₂)

Angolo di carico θ

== Deformazioni ==

Selezione delle distorsioni volumetriche nel navigatore

Selezione della distorsione volumetrica nel navigatore

Deformazioni sui solidi nella tabella

Nel navigatore, specificare quali deformazioni devono essere visualizzate sulle superfici di delimitazione dei volumi. La tabella elenca le deformazioni di queste superfici secondo le impostazioni specificate nel Manager delle tabelle dei risultati . Le deformazioni volumetriche sono suddivise nelle seguenti categorie: * Deformazioni totali di base * Deformazioni totali principali * Deformazioni totali equivalenti * Invarianti di deformazione Le '''deformazioni totali di base''' comprese le deformazioni di taglio vengono determinate direttamente dal nucleo di calcolo. Per lo stato di deformazione spaziale, la definizione generale del tensore è la seguente:

ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]

Tensore per lo stato di deformazione

Gli elementi del tensore sono definiti come segue:

ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})

Elementi tensori

Dalle deformazioni di base, vengono determinate le '''deformazioni totali principali''' ε₁, ε₂ e ε₃.

Suggerimento

Con la voce del navigatore '''ε₁₂₃''' è possibile rappresentare graficamente le traiettorie delle deformazioni principali.

Le '''deformazioni totali equivalenti''' ε_v vengono determinate nel modo seguente secondo quattro diverse ipotesi di tensione.

ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}

Deformazione totale comparativa_{v, Mises}

ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)

R	Matrice (vedi sotto)

Deformazione totale comparativa ε_v,Tresca (massimo delle differenze di autovalori secondo la matrice R)

ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)

R	Matrix (siehe unten)

Vergleichsgesamtdehnung ε_v,Rankine (Maximum der Eigenwerte gemäß Matrix R)

ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)

R	Matrice (vedi sotto)

Deformazione totale comparativa_v,Bach (massimo delle differenze di autovalori secondo la matrice R tenendo conto del rapporto di Poisson's)

R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]

Matrice R

Le '''invarianti di deformazione''' consentono una valutazione mirata dello stato di deformazione. Dalle deformazioni principali viene determinata l'invariante volumetrica della deformazione ε_v:

ε_{v} = ε_{11} + ε_{22} + ε_{33}

Invariante di deformazione volumetrica ε_v

Le deformazioni di taglio ε_q vengono calcolate come segue:

ε_{q} = \frac{1}{3} \sqrt{2 [{(ε_{11} - ε_{22})}^{2} + {(ε_{22} - ε_{33})}^{2} + {(ε_{33} - ε_{11})}^{2}] + 3 (2 {ε_{12}}^{2} + 2 {ε_{23}}^{2} + 2 {ε_{31}}^{2})}

Deformazione da taglio ε_q

Capitolo principale

Risultati