Zurück zu Online-Handbüchern

2381x

000483

Dipl.-Ing. (FH) Robert Vogl

27. April 2023

Handbuch wählen

Übersicht

Benutzeroberfläche und Einstellungen

Dlubal Center

Modell-Basisangaben

Struktur

Imperfektionen

Lastfälle und Kombinationen

Lastassistenten

Lasten

Ergebnisobjekte

Berechnung

Ergebnisse

Hilfsobjekte

Programmfunktionen

Ergebnisauswertung

Ausdruckprotokolle

Ergebnisse volumenweise

Sie können die Ergebnisse für Volumen grafisch über die Navigator-Kategorie Volumenkörper anzeigen. Die numerischen Volumenergebnisse finden Sie in der Tabellen-Kategorie Ergebnisse volumenweise.

Ergebnisse volumenweise in Tabelle

Info

In der Tabelle und in der Grafik werden die Ergebnisse angezeigt, die an den Begrenzungsflächen des Volumenkörpers vorliegen. Um die Ergebnisse im Inneren des Volumenkörpers zu überprüfen, aktivieren Sie in der unteren Kategorie Werte an Flächen die Option An FE-Netzpunkten. Die Werte im Volumenkörper können Sie dann über eine Clippingebene ablesen (siehe Kapitel Clippingebenen).

Verformungen

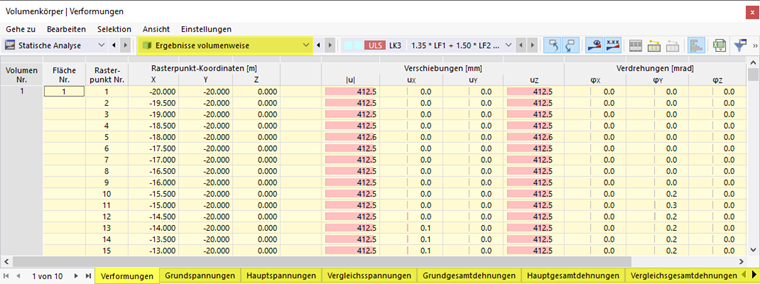
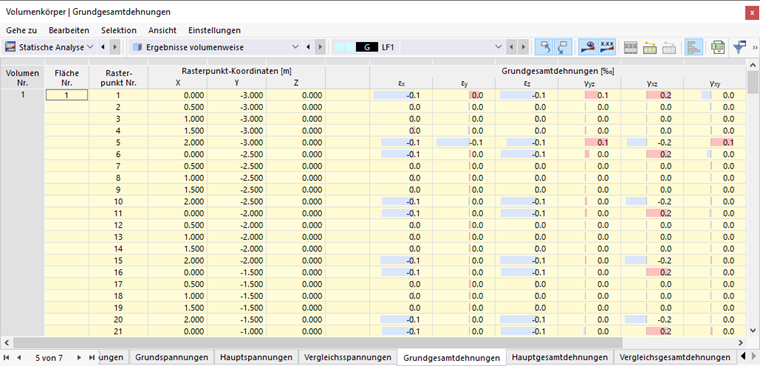
Das Bild Ergebnisse volumenweise in Tabelle zeigt die Tabelle mit den Verformungen der Begrenzungsflächen. Die Verschiebungen und Verdrehungen werden in den Flächen-Rasterpunkten ausgegeben (siehe Kapitel Flächen ).

Tipp

Bei kleinen Flächen kann die Standardmaschenweite des Rasters von 0.5 m dazu führen, dass nur wenige Rasterpunkte existieren. Passen Sie in diesem Fall die Anzahl oder den Abstand der Rasterpunkte an die Flächengröße an.

Die Verformungen bedeuten:

\|u\|	Absolutwert der Gesamtverschiebung
u_X	Verschiebung in Richtung der globalen X-Achse
u_Y	Verschiebung in Richtung der globalen Y-Achse
u_Z	Verschiebung in Richtung der globalen Z-Achse
φ_X	Verdrehung um die globale X-Achse
φ_Y	Verdrehung um die globale Y-Achse
φ_Z	Verdrehung um die globale Z-Achse

Spannungen

Volumenspannungen im Navigator auswählen

Spannungen der Volumen in Tabelle

Legen Sie im Navigator fest, welche Spannungen an den Begrenzungsflächen der Volumen angezeigt werden sollen. Die Tabelle listet die Spannungen dieser Flächen nach den Vorgaben auf, die im Ergebnistabellen-Manager festgelegt sind.

Die Volumenspannungen sind in folgende Kategorien unterteilt:

Grundspannungen
Hauptspannungen
Vergleichsspannungen
Spannungsinvarianten

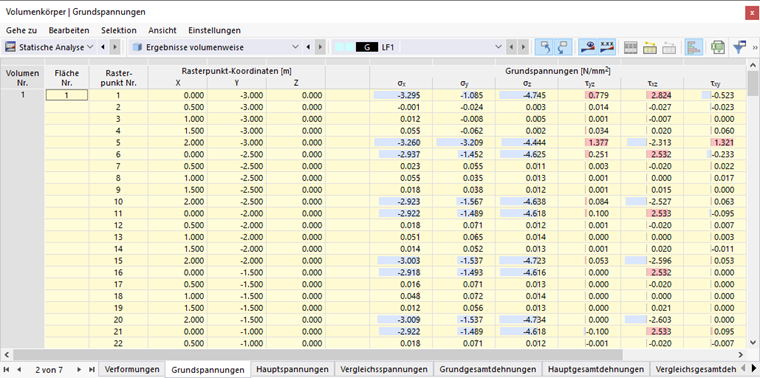
Grundspannungen

Volumenspannungen lassen sich nicht wie Flächenspannungen mit einfachen Gleichungen beschreiben. Die Grundspannungen σ_x, σ_y und σ_z einschließlich der Schubspannungen τ_yz, τ_xz und τ_xy werden direkt vom Rechenkern ermittelt.

Wird ein Würfel mit den Kantenlängen d_x, d_y und d_z aus einem mehrachsig beanspruchten Körper herausgeschnitten, so können die Spannungen in jeder Würfelfläche in Normal- und Schubspannungen zerlegt werden. Unter Vernachlässigung der Raumkraft und auch der Spannungsunterschiede an parallelen Flächen lässt sich im lokalen Koordinatensystem des Würfels der Spannungszustand durch neun Spannungskomponenten beschreiben.

Volumenelement mit Spannungskomponenten

Die Matrix des Spannungstensors lautet:

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Matrix des Spannungstensors

Hauptspannungen

Aus den Eigenwerten des Tensors ergeben sich die Hauptspannungen σ₁, σ₂ und σ₃ wie folgt:

\det (S - σ E) = 0

E	3x3 Einheitsmatrix

Hauptspannungen

Die maximale Schubspannung τ_max wird nach dem Mohrschen Spannungskreis bestimmt:

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Maximale Schubspannung

Tipp

Mit dem Navigatoreintrag σ₁₂₃ können Sie die Trajektorien der Hauptspannungen grafisch darstellen.

Vergleichsspannungen

Die Vergleichsspannungen σ_v nach von Mises lassen sich durch zwei gleichwertige Formeln bestimmen.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Vergleichsspannung σ_v,Mises aus Hauptspannungen

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Vergleichsspannung σ_v,Mises aus Grundspannungen

Für die Ermittlung der Vergleichsspannung σ_v nach Tresca werden die Differenzen aus den Hauptspannungen untersucht, um daraus den Maximalwert zu bestimmen.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Vergleichsspannung σ_v,Tresca

Die Vergleichsspannung σ_v nach Rankine ermittelt sich aus den größten Absolutwerten der Hauptspannungen.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Vergleichsspannung σ_v,Rankine

Zur Ermittlung der Vergleichsspannung σ_v nach Bach werden die Hauptspannungsdifferenzen unter Berücksichtigung der Querdehnzahl ν untersucht, um daraus den Maximalwert zu bestimmen.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Vergleichsspannung σ_v,Bach

Spannungsinvarianten

Spannungsinvarianten ermöglichen eine koordinatenunabhängige und somit objektive Beschreibung des Spannungszustands eines Materials. Als skalare Größen bleiben sie unter beliebigen Drehungen des Koordinatensystems unverändert und erfassen die physikalisch relevanten Eigenschaften dieser Zustände unabhängig von der gewählten Tensorrepräsentation. Ihre besondere Bedeutung liegt darin, dass viele mechanische Phänomene – insbesondere plastisches Fließen, Versagen und Bruch – nicht von einzelnen Spannungskomponenten, sondern von invarianten Maßzahlen abhängen. Damit bilden Spannungsinvarianten die Grundlage zahlreicher etablierter Fließ- und Versagenskriterien, wie etwa der von Mises-, der Tresca- oder der Drucker-Prager-Theorie.

Die mittlere Spannung p ist mit der ersten Spannungsinvariante I₁ verknüpft und beschreibt die hydrostatische Spannung. Sie ergibt sich aus dem arithmetischen Mittel der drei Hauptspannungen und bildet den Abstand des Spannungspunkts vom Koordinatenursprung auf der Raumdiagonalen ab.

p = \frac{σ_{1} + σ_{2} + σ_{3}}{3} = \frac{I_{1}}{3}

σ₁ , σ₂ , σ₃	Hauptspannungen
I₁	Erste Spannungsinvariante

Mittlere Spannung p

Sie charakterisiert den mittleren Normalspannungszustand und ist maßgeblich für Volumenänderungen verantwortlich. Physikalisch entspricht p einem gleichmäßigen Druck- bzw. Zugzustand, der keine Formänderung, sondern ausschließlich Kompression oder Dilatation bewirkt. In vielen Materialien, insbesondere in der Boden- und Gesteinsmechanik sowie in druckempfindlichen Werkstoffen, beeinflusst p wesentlich das Festigkeits- und Verformungsverhalten.

Die deviatorische Spannung q ist mit der zweiten Invariante des Spannungsdeviators J₂ verknüpft. Sie ermittelt sich wie folgt:

q = \sqrt{{σ_{1}}^{2} + {σ_{2}}^{2} + {σ_{3}}^{2} - σ_{1} σ_{2} - σ_{2} σ_{3} - σ_{3} σ_{1}}

= \frac{1}{\sqrt{2}} \sqrt{{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}} = \sqrt{{I_{1}}^{2} - 3 I_{2}} = \sqrt{3 J_{2}}

I₁	Erste Spannungsinvariante
I₂	Zweite Spannungsinvariante
J₂	Zweite deviatorische Spannungsinvariante

Deviatorische Spannung q

Sie beschreibt den Anteil des Spannungszustands, der für Formänderungen (Scherverzerrungen) verantwortlich ist, ohne das Volumen zu ändern. Der deviatorische Anteil treibt insbesondere plastisches Fließen und Versagen in duktilen Materialien an. Das von Mises-Fließkriterium basiert direkt auf J₂ bzw. q und verdeutlicht, dass plastische Deformation primär durch deviatorische Spannungen kontrolliert wird.

Der Lode-Winkel θ gibt die Lage des Spannungspunktes in der Deviatorebene an. Die Deviatorebene wird in sechs Sektoren aufgeteilt, sodass −30° ≤ θ ≤ 30° gilt. Der Winkel wird wie folgt bestimmt:

θ = \frac{1}{3} \sin^{- 1} (- \frac{3 \sqrt{3}}{2} \frac{J_{3}}{{J_{2}}^{3 / 2}})

J₂	Zweite deviatorische Spannungsinvariante: 1/6 [(σ₁ – σ₂)² + (σ₂ – σ₃)² + (σ₃ – σ₁)²]
J₃	Dritte deviatorische Spannungsinvariante: 1/27 (2σ₁ – σ₂ – σ₃) (2σ₂ – σ₃ – σ₁) (2σ₃ – σ₁ – σ₂)

Lode-Winkel θ

Eine reine Schubbeanspruchung ergibt sich für θ = 0, während für θ = 30° der Spannungszustand σ₁ > σ₂ = σ₃ entsteht, der einem triaxialen Kompressionsversuch entspricht. Aus θ = −30° resultiert der Spannungszustand eines triaxialen Zugversuchs mit σ₁ < σ₂ = σ₃.

Verzerrungen

Volumenverzerrungen im Navigator auswählen

Dehnungen der Volumen in Tabelle

Legen Sie im Navigator fest, welche Verzerrungen an den Begrenzungsflächen der Volumen angezeigt werden sollen. Die Tabelle listet die Dehnungen dieser Flächen nach den Vorgaben auf, die im Ergebnistabellen-Manager festgelegt sind.

Die Volumenverzerrungen sind in folgende Kategorien unterteilt:

Grundgesamtdehnungen
Hauptgesamtdehnungen
Vergleichsgesamtdehnungen
Dehnungsinvarianten

Grundgesamtdehnungen

Die Grundgesamtdehnungen einschließlich der Schubverzerrungen werden direkt vom Rechenkern ermittelt. Für den räumlichen Verzerrungszustand lautet die allgemeine Definition des Tensors:

ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]

Tensor für Verzerrungszustand

Die Elemente des Tensors sind wie folgt definiert:

ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})

Tensorelemente

Hauptgesamtdehnungen

Aus den Grunddehnungen werden die Hauptgesamtdehnungen ε₁, ε₂ und ε₃ ermittelt.

Tipp

Mit dem Navigatoreintrag ε₁₂₃ können Sie die Trajektorien der Hauptdehnungen grafisch darstellen.

Vergleichsgesamtdehnungen

Die Vergleichsgesamtdehnungen ε_v werden wie folgt nach vier verschiedenen Spannungshypothesen ermittelt.

ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}

Vergleichsgesamtdehnung ε_v,Mises

ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)

R	Matrix (siehe unten)

Vergleichsgesamtdehnung ε_v,Tresca (Maximum der Eigenwertdifferenzen gemäß Matrix R)

ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)

R	Matrix (siehe unten)

Vergleichsgesamtdehnung ε_v,Rankine (Maximum der Eigenwerte gemäß Matrix R)

ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)

R	Matrix (siehe unten)

Vergleichsgesamtdehnung ε_v,Bach (Maximum der Eigenwertdifferenzen gemäß Matrix R unter Berücksichtigung der Querdehnzahl ν)

R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]

Matrix R

Dehnungsinvarianten

Dehnungsinvarianten sind Kennwerte des Dehnungstensors, die unabhängig von der Orientierung des Koordinatensystems bleiben. Sie ermöglichen eine klare Trennung zwischen Volumenänderung und Formänderung eines Materials. Die Unterscheidung ist zentral für die Analyse von Materialverhalten, Festigkeitskriterien und Plastizitätsmodellen.

Die volumetrische Dehnungsinvariante ε_v entspricht dem isotropen Anteil der Gesamtdehnungen. Sie wird aus den Hauptdehnungen ermittelt:

ε_{v} = ε_{11} + ε_{22} + ε_{33}

Volumetrische Dehnungsinvariante ε_v

Die deviatorische Dehnungen ε_q oder auch Scherdehnungen γ_s beschreiben die reine Formänderung ohne Volumenänderung. Sie ermitteln sich wie folgt:

ε_{q} = \frac{1}{3} \sqrt{2 [{(ε_{11} - ε_{22})}^{2} + {(ε_{22} - ε_{33})}^{2} + {(ε_{33} - ε_{11})}^{2}] + 3 (2 {ε_{12}}^{2} + 2 {ε_{23}}^{2} + 2 {ε_{31}}^{2})}

Scherdehnung ε_q

Übergeordnetes Kapitel

Ergebnisse