Volver a manuales en línea

2360x

000483

Dipl.-Ing. (FH) Robert Vogl

27-04-2023

Seleccionar manual

Visión de conjunto

Interfaz gráfica de usuario y configuración

Dlubal Center

Datos básicos del modelo

Estructura

Imperfecciones

Casos de carga y combinaciones

Asistentes de carga

Cargas

Objetos de resultado

Cálculo

Resultados

Objetos auxiliares

Funciones del programa

Evaluación de resultados

Informes

Resultados por sólido

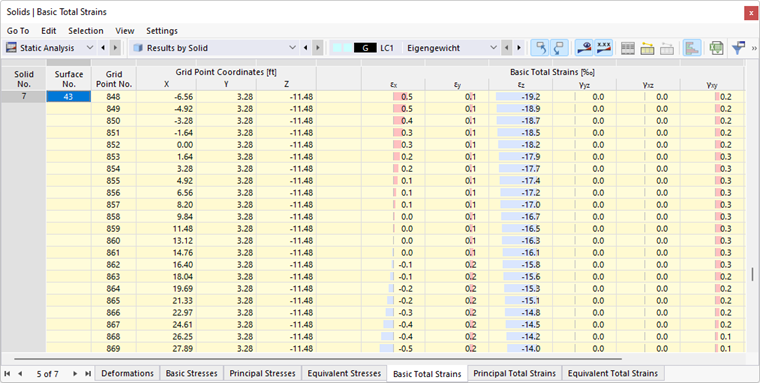
Puede mostrar los resultados para el volumen gráficamente a través de la categoría del navegador Cuerpo de volumen. Los resultados numéricos del volumen se pueden encontrar en la categoría de tabla Resultados por volumen.

Resultados por sólido en la tabla

Información

En la tabla y en el gráfico se muestran los resultados presentes en las superficies delimitadoras del cuerpo de volumen. Para verificar los resultados dentro del cuerpo de volumen, active la opción En puntos de la malla FE en la categoría inferior Valores en superficies. Luego, puede leer los valores dentro del cuerpo de volumen a través de un plano de recorte (ver capítulo Planos de recorte).

Deformaciones

La imagen Resultados por volumen en tabla muestra la tabla con las deformaciones de las superficies delimitadoras. Los desplazamientos y torsiones se presentan en los puntos de cuadrícula de las superficies (ver capítulo Superficies ).

Consejo

En superficies pequeñas, la cuadrícula estándar de 0.5 m puede resultar en solo unos pocos puntos de cuadrícula. En este caso, ajuste la cantidad o la distancia entre los puntos de la cuadrícula al tamaño de la superficie.

Las deformaciones significan:

\|u\|	Valor absoluto del desplazamiento total
u_X	Desplazamiento en dirección del eje X global
u_Y	Desplazamiento en dirección del eje Y global
u_Z	Desplazamiento en dirección del eje Z global
φ_X	Rotación alrededor del eje X global
φ_Y	Rotación alrededor del eje Y global
φ_Z	Rotación alrededor del eje Z global

Tensiones

Seleccionar tensiones de sólidos en el navegador

Tensiones de sólidos en tabla

Especifique en el navegador qué tensiones se deben mostrar en las superficies delimitadoras del volumen. La tabla lista las tensiones de estas superficies según las especificaciones establecidas en el Gestor de tablas de resultados .

Las tensiones de volumen están categorizadas en:

Tensiones básicas
Tensiones principales
Tensiones equivalentes
Invariantes de tensión

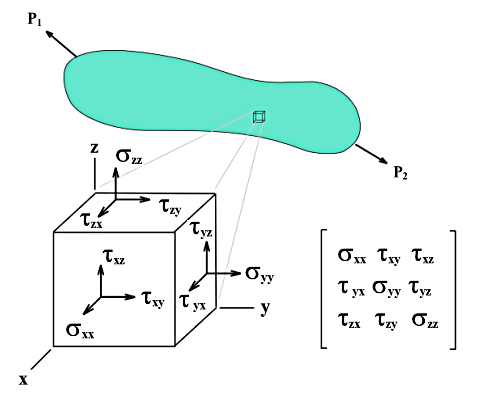
Las tensiones de volumen no se pueden describir como las tensiones de superficie con ecuaciones simples. Las tensiones básicas σ_x, σ_y y σ_z incluyendo las tensiones de corte τ_yz, τ_xz y τ_xy son determinadas directamente por el núcleo de cálculo.

Si se corta un cubo con las dimensiones d_x, d_y y d_z de un cuerpo sujeto a múltiples cargas, las tensiones en cada cara del cubo se pueden descomponer en tensiones normales y de corte. Despreciando las fuerzas del espacio y también la diferencia de tensiones en superficies paralelas, el estado de tensión local en el sistema de coordenadas del cubo se puede describir por nueve componentes de tensión.

Elemento de un sólido con los componentes de la tensión

La matriz del tensor de tensión se expresa como:

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Matriz del tensor de tensiones

A partir de los valores propios del tensor, se determinan las tensiones principales σ₁, σ₂ y σ_{3> de la siguiente manera:}

\det (S - σ E) = 0

E	3x3 Einheitsmatrix

Tensiones principales

La '''tensión de corte''' máxima τ_max se determina según el círculo de tensión de Mohr:

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Tensión tangencial máxima

Consejo

Con la entrada del navegador '''σ₁₂₃''', puede representar gráficamente las trayectorias de las tensiones principales.

Las '''tensiones equivalentes''' σ_v según von Mises se pueden determinar con dos ecuaciones equivalentes.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Tensión equivalente σ_v,Mises de las tensiones principales

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Tensión equivalente σ_v,Mises de las tensiones básicas

Para determinar la tensión equivalente σ_v según Tresca , se evalúan las diferencias entre las tensiones principales para determinar el valor máximo.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Tensión equivalente σ_v,Tresca

La tensión equivalente σ_v según Rankine se calcula a partir de los mayores valores absolutos de las tensiones principales.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Tensión equivalente σ_v,Rankine

Para determinar la tensión equivalente σ_v según Bach , se evalúan las diferencias entre las tensiones principales con consideración del coeficiente de Poisson ν para encontrar el valor máximo.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Tensión equivalente σ_v,Bach

Las '''invariantes de tensión''' permiten una evaluación específica del estado de tensión. A partir de las tensiones principales, se determina la tensión media p:

p = \frac{σ_{1} + σ_{2} + σ_{3}}{3} = \frac{I_{1}}{3}

σ₁ , σ₂ , σ₃	Tensiones principales
I₁	Primer invariante de tensión

Presión media p

La tensión deviatórica q se calcula como sigue:

q = \sqrt{{σ_{1}}^{2} + {σ_{2}}^{2} + {σ_{3}}^{2} - σ_{1} σ_{2} - σ_{2} σ_{3} - σ_{3} σ_{1}}

= \frac{1}{\sqrt{2}} \sqrt{{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}} = \sqrt{{I_{1}}^{2} - 3 I_{2}} = \sqrt{3 J_{2}}

I₁	Primer invariante de tensiones
I₂	Segundo invariante del esfuerzo
J₂	Segunda invariante del esfuerzo desviador

Esfuerzo de desviación q

El ángulo de Lode θ se puede considerar como una medida del tipo de carga. Varía entre -30° y +30° y se determina de la siguiente manera:

θ = \frac{1}{3} \sin^{- 1} (- \frac{3 \sqrt{3}}{2} \frac{J_{3}}{{J_{2}}^{3 / 2}})

J₂	Segunda invariante de tensión desviadora: 1/6 [(σ₁ – σ₂)² + (σ₂ – σ₃)² + (σ₃ – σ₂)²]
J₃	Invariante de tensión desviadora de tercer orden: 1/27 (2σ₁ – σ₂ – σ₃) (2σ₂ – σ₃ – σ₁) (2σ₃ – σ₁ – σ₂)

Ángulo de Lode θ

== Deformaciones ==

Seleccionar distorsiones volumétricas en el Navegador

Deformaciones en sólidos en la tabla

Especifique en el navegador qué deformaciones se deben mostrar en las superficies delimitadoras del volumen. La tabla lista las deformaciones de estas superficies según las especificaciones establecidas en el Gestor de tablas de resultados . Las deformaciones de volumen están categorizadas en: * Deformaciones básicas totales * Deformaciones principales totales * Deformaciones equivalentes totales * Invariantes de deformación Las '''deformaciones básicas totales''', incluyendo las deformaciones de corte, son determinadas directamente por el núcleo de cálculo. Para el estado de deformación espacial, la definición general del tensor es:

ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]

Tensor para el estado de deformación

Los elementos del tensor se definen como sigue:

ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})

Elementos tensores

De las deformaciones básicas se obtienen las '''deformaciones principales totales''' ε₁, ε₂ y ε₃.

Consejo

Con la entrada del navegador '''ε₁₂₃''', puede representar gráficamente las trayectorias de las deformaciones principales.

Las '''deformaciones equivalentes totales''' ε_v se determinan de la siguiente manera según cuatro hipótesis de tensión diferentes.

ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}

Deformación total comparativa ε_v,Mises

ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)

R	Matriz (ver a continuación)

Deformación total comparativa ε_v,Tresca (la máxima diferencia entre valores propios según la matriz R)

ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)

R	Matrix (siehe unten)

Deformación total comparativa ε_v,Rankine (la máxima diferencia entre valores propios según la matriz R)

ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)

R	Matriz (ver a continuación)

Deformación total comparativa ε_v,Bach (la máxima diferencia entre valores propios según la matriz R considerando el coeficiente de Poisson ν)

R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]

Matriz R

Las '''invariantes de deformación''' permiten una evaluación específica del estado de deformación. A partir de las deformaciones principales, se determina la invariante de deformación volumétrica ε_v:

ε_{v} = ε_{11} + ε_{22} + ε_{33}

Invariante de deformación volumétrica ε_v

Las deformaciones de corte ε_q se calculan como sigue:

ε_{q} = \frac{1}{3} \sqrt{2 [{(ε_{11} - ε_{22})}^{2} + {(ε_{22} - ε_{33})}^{2} + {(ε_{33} - ε_{11})}^{2}] + 3 (2 {ε_{12}}^{2} + 2 {ε_{23}}^{2} + 2 {ε_{31}}^{2})}

Deformación por cortante ε_q

Capítulo principal

Resultados