Powrót do Instrukcji online

2380x

000483

Dipl.-Ing. (FH) Robert Vogl

2023-04-27

Wybór ręczny

Przegląd

Graficzny interfejs użytkownika i jego ustawienia

Dlubal Center

Dane podstawowe modelu

Konstrukcja

Imperfekcje

Przypadki obciążeń i kombinacje

Asystenci obciążeń

Obciążenia

Obiekty wynikowe

Obliczenia

Wyniki

Obiekty pomocnicze

Funkcje programu

Wizualizacja wyników

Raport

Wyniki według brył

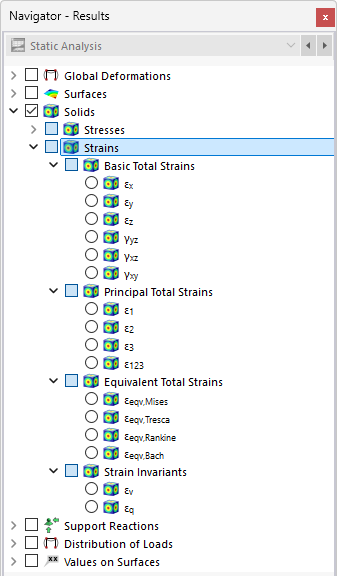
Możesz wyświetlić wyniki dla objętości graficznie przez kategorię nawigatora Ciało stałe. Numeryczne wyniki objętości znajdziesz w kategorii tabeli Wyniki dla objętości.

Wyniki w tabeli według brył

Informacje

W tabeli i na grafice wyświetlane są wyniki występujące na powierzchniach ograniczających ciała stałego. Aby sprawdzić wyniki wewnątrz ciała stałego, w dolnej kategorii Wartości na powierzchniach aktywuj opcję W węzłach siatki MES. Wartości wewnątrz ciała stałego można wtedy odczytać za pomocą płaszczyzny przycinania (zobacz rozdział Płaszczyzny przycinania).

Deformacje

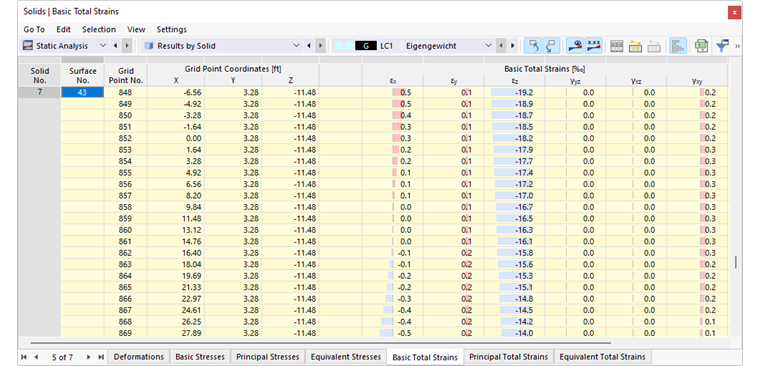
Obraz Wyniki dla objętości w tabeli pokazuje tabelę z deformacjami powierzchni ograniczających. Przemieszczenia i obroty są podawane w punktach siatki powierzchni (zobacz rozdział Powierzchnie ).

Wskazówka

Dla małych powierzchni standardowa gęstość siatki o rozstawie 0,5 m może prowadzić do istnienia jedynie kilku punktów siatki. W takim przypadku dostosuj liczbę lub rozstaw punktów siatki do rozmiaru powierzchni.

Deformacje oznaczają:

\|u\|	Wartość absolutna całkowitego przemieszczenia
u_X	Przemieszczenie w kierunku globalnej osi X
u_Y	Przemieszczenie w kierunku globalnej osi Y
u_Z	Przemieszczenie w kierunku globalnej osi Z
φ_X	Obrót wokół globalnej osi X
φ_Y	Obrót wokół globalnej osi Y
φ_Z	Obrót wokół globalnej osi Z

Naprężenia

Wybór naprężeń brył w nawigatorze

Naprężenia brył w tabeli

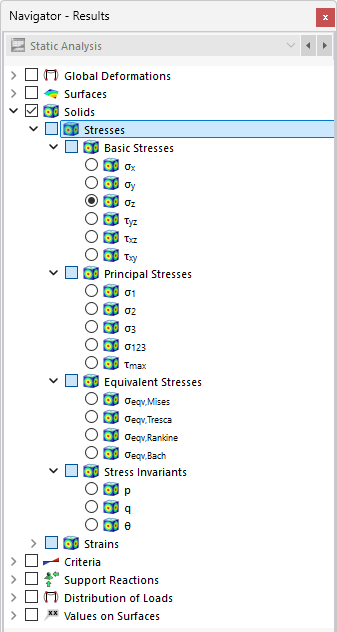
Ustal w nawigatorze, jakie naprężenia mają być wyświetlane na powierzchniach ograniczających objętości. Tabela wylicza naprężenia tych powierzchni zgodnie z ustaleniami w Menedżer tablic wyników .

Naprężenia objętości są podzielone na następujące kategorie:

Naprężenia podstawowe
Naprężenia główne
Naprężenia zastępcze
Niezmienniki naprężeń

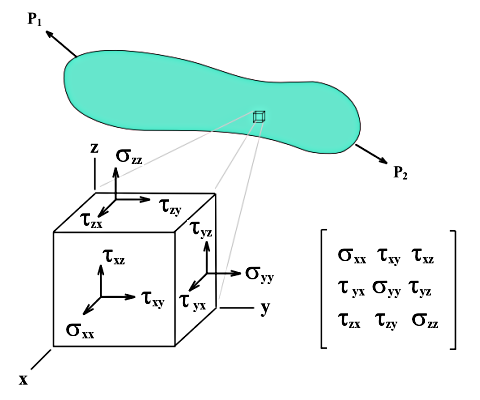
Naprężenia objętości nie można opisać prostymi równaniami jak naprężenia na powierzchniach. Naprężenia podstawowe σ_x, σ_y i σ_z oraz naprężenia ścinające τ_yz, τ_xz i τ_xy są określane bezpośrednio przez rdzeń obliczeniowy.

Jeśli sześcian o krawędziach d_x, d_y i d_z zostanie wycięty z ciała obciążonego wieloosiowo, to naprężenia na każdej powierzchni sześcianu można rozłożyć na naprężenia normalne i ścinające. Pomijając siły powierzchniowe i różnice naprężeń na powierzchniach równoległych, stan naprężenia w lokalnym układzie współrzędnych sześcianu można opisać dziewięcioma składowymi naprężenia.

Volumenelement mit Spannungskomponenten

Macierz tensora naprężenia to:

S = [\begin{matrix} σ_{x} & τ_{xy} & τ_{xz} \\ τ_{yx} & σ_{y} & τ_{yz} \\ τ_{zx} & τ_{zy} & σ_{z} \end{matrix}]

Macierz tensora naprężeń

Z wartości własnych tensora wynikają naprężenia główne σ₁, σ₂ i σ_{3> w następujący sposób:}

\det (S - σ E) = 0

E	3x3 Einheitsmatrix

Naprężenia główne

Maksymalne '''naprężenie ścinające''' τ_max jest określane za pomocą koła naprężeń Mohr’a:

τ_{\max} = \frac{1}{2} (σ_{1} - σ_{3})

Max naprężenie styczne

Wskazówka

Z wpisem nawigatora '''σ₁₂₃''' możesz graficznie wyświetlić trajektorie naprężeń głównych.

'''Naprężenia zastępcze''' σ_v według von Mises wyznaczane są za pomocą dwóch równoważnych formuł.

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Naprężenie równoważne σ_{v, Mises} z naprężeń głównych

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Naprężenie równoważne σ_v,Mises z naprężeń podstawowych

Dla określenia naprężenia zastępczego σ_v według Tresca bada się różnice pomiędzy naprężeniami głównymi w celu wyznaczenia maksymalnej wartości.

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Naprężenie równoważne σ_{v, Tresca}

Naprężenie zastępcze σ_v według Rankine oblicza się z najwięszych wartości absolutnych naprężeń głównych.

σ_{v, Rankine} = max (|σ_{1}|; |σ_{2}|; |σ_{3}|)

Naprężenie równoważne σ_v,Rankine

Do ustalenia naprężenia zastępczego σ_v według Bacha bada się różnice naprężeń głównych z uwzględnieniem wartość charakterystycznej liczby, aby określić maksymalną wartość.

σ_{v, Bach} = max [|σ_{1} - ν (σ_{2} + σ_{3})|; |σ_{2} - ν (σ_{3} + σ_{1})|; |σ_{3} - ν (σ_{1} + σ_{2})|]

Naprężenie równoważne σ_{v, Bach}

'''Niezmienniki naprężeń''' umożliwiają szczegółową ocenę stanu naprężenia. Z naprężeń głównych oblicza się średnie naprężenie p:

p = \frac{σ_{1} + σ_{2} + σ_{3}}{3} = \frac{I_{1}}{3}

σ₁ , σ₂ , σ₃	Naprężenia główne
I₁	Pierwsza niezmiennicza naprężenia

Średnie naprężenie p

Naprężenie dewiacyjne q jest określane w następujący sposób:

q = \sqrt{{σ_{1}}^{2} + {σ_{2}}^{2} + {σ_{3}}^{2} - σ_{1} σ_{2} - σ_{2} σ_{3} - σ_{3} σ_{1}}

= \frac{1}{\sqrt{2}} \sqrt{{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}} = \sqrt{{I_{1}}^{2} - 3 I_{2}} = \sqrt{3 J_{2}}

I₁	Pierwsza niezmiennicza naprężeniowa
I₂	Drugi niezmiennik naprężenia
J₂	Drugi niezmiennik naprężeń dewiacyjnych

Naprężenie dewiacyjne q

Kąt Lode’a (θ) może być uznawany za miarę charakteru obciążenia. Zawiera się w przedziale od -30° do +30° i określa się go następująco:

θ = \frac{1}{3} \sin^{- 1} (- \frac{3 \sqrt{3}}{2} \frac{J_{3}}{{J_{2}}^{3 / 2}})

J₂	Drugi niezmiennik naprężenia dewiatora: 1/6 [(σ₁ – σ₂)² + (σ₂ – σ₃)² + (σ₃ – σ₂)²]
J₃	Trzecia niezmiennicza naprężenia dewiacyjnego: 1/27 (2σ₁ – σ₂ – σ₃) (2σ₂ – σ₃ – σ₁) (2σ₃ – σ₁ – σ₂)

Kąt Lode'a θ

== Odkształcenia ==

Wybór odkształceń objętościowych w nawigatorze

Odkształcenia na bryłach w tabeli

Ustal w nawigatorze, jakie odkształcenia mają być wyświetlane na powierzchniach ograniczających objętości. Tabela wylistuje przemieszczenia tych powierzchni zgodnie z ustaleniami w Menedżer tablic wyników . Odkształcenia objętości są podzielone na następujące kategorie: * Podstawowe całkowite odkształcenia * Główne całkowite odkształcenia * Zastępcze całkowite odkształcenia * Niezmienniki odkształceń '''Podstawowe całkowite odkształcenia''' w tym ścinające są określane bezpośrednio przez rdzeń obliczeniowy. Ogólna definicja tensora dla przestrzennego stanu odkształcenia jest następująca:

ε = [\begin{matrix} ε_{x x} & ε_{x y} & ε_{x z} \\ ε_{y x} & ε_{y y} & ε_{y z} \\ ε_{z x} & ε_{z y} & ε_{z z} \end{matrix}]

Tensor stanu odkształcenia

Elementy tensora są zdefiniowane następująco:

ε_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})

Elementy tensorowe

Z podstawowych odkształceń są określane '''główne całkowite odkształcenia''' ε₁, ε₂ i ε₃.

Wskazówka

Z wpisem nawigatora '''ε₁₂₃''' możesz graficznie wyświetlić trajektorie głównych odkształceń.

'''Zastępcze całkowite odkształcenia''' ε_v są określane według czterech różnych hipotez naprężenia, jak pokazano poniżej.

ε_{v, Mises} = \frac{1}{1 + ν} \sqrt{{ε_{x}}^{2} + {ε_{y}}^{2} + {ε_{z}}^{2} - ε_{x} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x} + \frac{3}{4} ({γ_{x y}}^{2} + {γ_{y z}}^{2} + {γ_{x z}}^{2})}

Porównawcze odkształcenie całkowite ε_v,Mises

ε_{v, Tresca} = \max (|R_{1} - R_{2}|; |R_{2} - R_{3}|; |R_{3} - R_{1}|)

R	Macierz (patrz niżej)

Porównawcze odkształcenie całkowite ε_v,Tresca (maksimum różnic wartości własnych według macierzy R)

ε_{v, Rankine} = \max (|R_{1}|; |R_{2}|; |R_{3}|)

R	Matrix (siehe unten)

Vergleichsgesamtdehnung ε_v,Rankine (Maximum der Eigenwerte gemäß Matrix R)

ε_{v, Bach} = \max (|R_{1} - ν (R_{2} + R_{3})|; |R_{2} - ν (R_{3} + R_{1})|; |R_{3} - ν (R_{1} + R_{2})|)

R	Macierz (patrz niżej)

Porównawcze odkształcenie całkowite ε_v,Bacha (maksymalne różnice wartości własnych według macierzy R uwzględniające współczynnik Poissona ν)

R = \frac{1}{1 + ν} [\begin{matrix} \frac{(1 - ν) ε_{x} + ν (ε_{y} + ε_{z})}{1 - 2 ν} & \frac{γ_{x y}}{2} & \frac{γ_{x z}}{2} \\ \frac{γ_{x y}}{2} & \frac{(1 - ν) ε_{y} + ν (ε_{x} + ε_{z})}{1 - 2 ν} & \frac{γ_{y z}}{2} \\ \frac{γ_{x z}}{2} & \frac{γ_{y z}}{2} & \frac{(1 - ν) ε_{z} + ν (ε_{x} + ε_{z})}{1 - 2 ν} \end{matrix}]

Macierz R

'''Niezmienniki odkształceń''' pozwalają na szczegółową ocenę stanu odkształcenia. Z odkształceń głównych wyznacza się wolumetryczny niezmiennik odkształcenia ε_v:

ε_{v} = ε_{11} + ε_{22} + ε_{33}

Inwariant objętościowy odkształcenia ε_v

Szerokie odkształcenia ε_q są określane w następujący sposób:

ε_{q} = \frac{1}{3} \sqrt{2 [{(ε_{11} - ε_{22})}^{2} + {(ε_{22} - ε_{33})}^{2} + {(ε_{33} - ε_{11})}^{2}] + 3 (2 {ε_{12}}^{2} + 2 {ε_{23}}^{2} + 2 {ε_{31}}^{2})}

Odkształcenie postaciowe ε_q

Rozdział nadrzędny

Wyniki