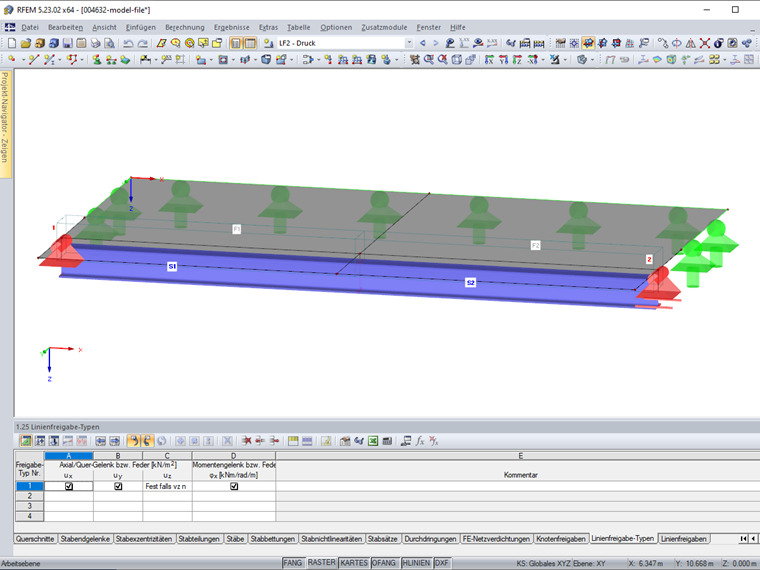
Im Bild 1 ist ein System dargestellt, in dem die Flächen 1 und 2 auf den Stäben 1 und 2 aufliegen sollen. Die Stäbe 1 und 2 sollen durch die Knotenlager 1 und 2 gelagert sein.
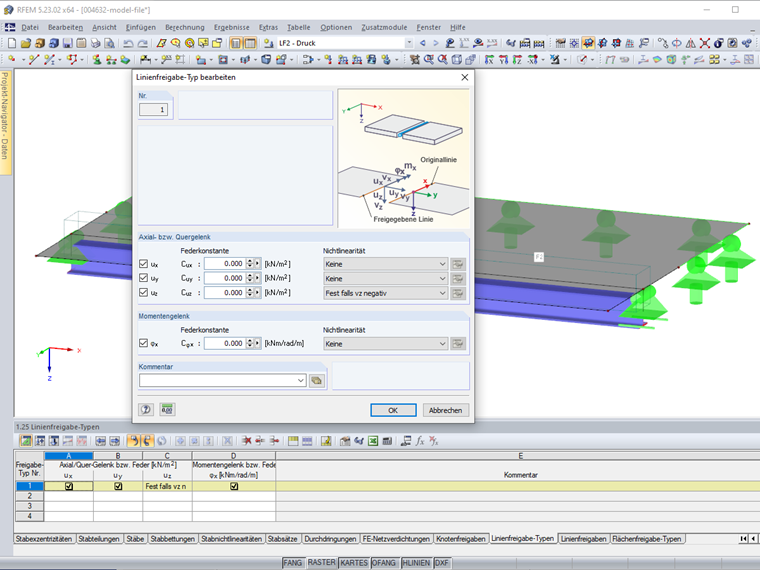
Für die Entkopplung der Stäbe von den Flächen ist der im Bild 2 dargestellte Linienfreigabe-Typ definiert. Die Verschiebung uz wird nur bei einer Zugkraft, die anderen Verschiebungen ux, uy sowie die Verdrehung φx werden immer freigegeben.
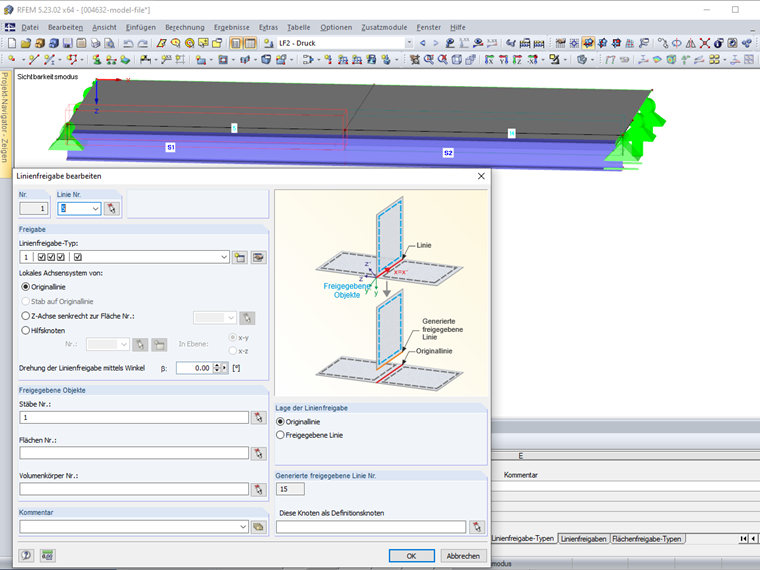
Die Linienfreigabe 1 ist an Linie 5 definiert und gibt den Stab 1 frei (Bild 3).
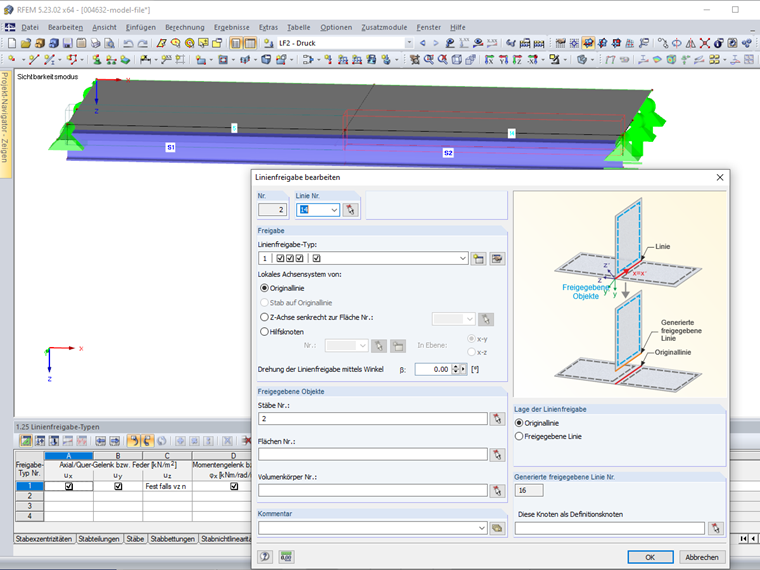
Die Linienfreigabe 2 ist an Linie 14 definiert und gibt den Stab 2 frei (Bild 4).
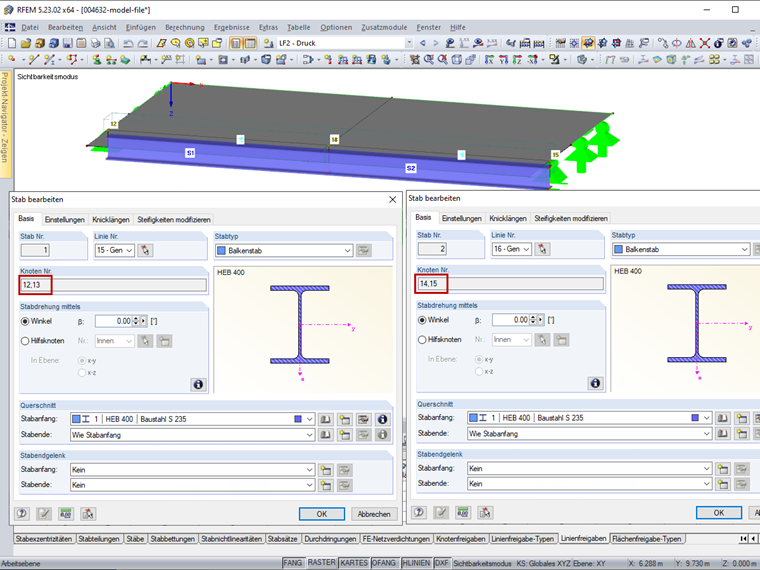
Stab 1 ist nun an der von der Linienfreigabe generierten Linie 15 mit den Knoten 12 und 13 und Stab 2 an der von der Linienfreigabe generierten Linie 16 mit den Knoten 14 und 15 definiert (Bild 5). Die Stäbe 1 und 2 haben an ihrem Schnittpunkt unterschiedliche Knoten (13 und 14) und sind damit nicht verbunden.
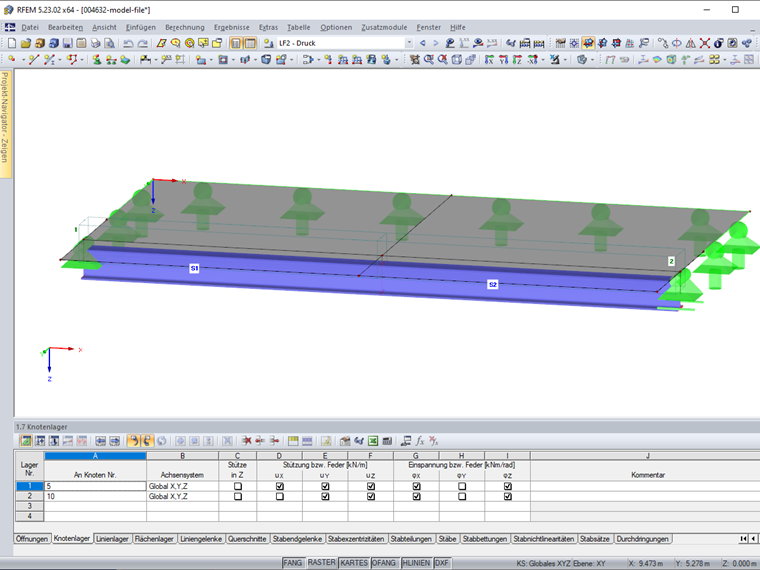
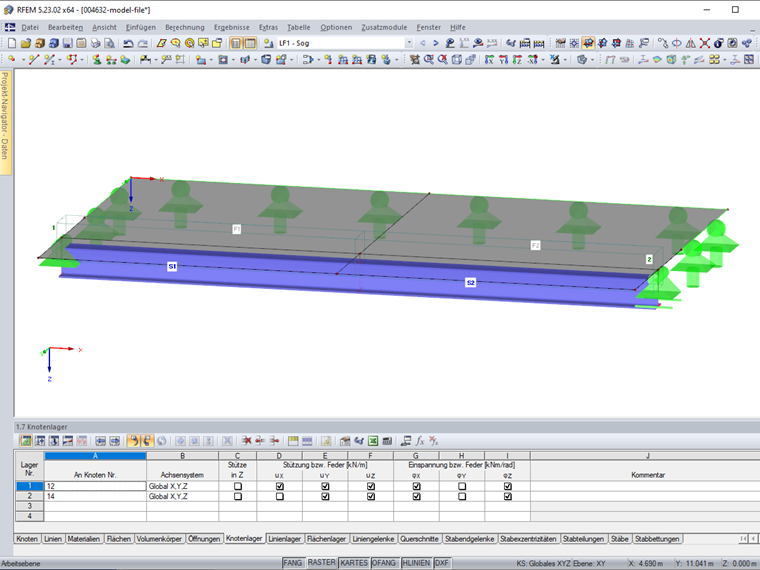
Des Weiteren sind die Knotenlager 1 und 2 an den Knoten 5 und 10 definiert und lagern damit die Flächen jedoch nicht die Stäbe (Bild 6).
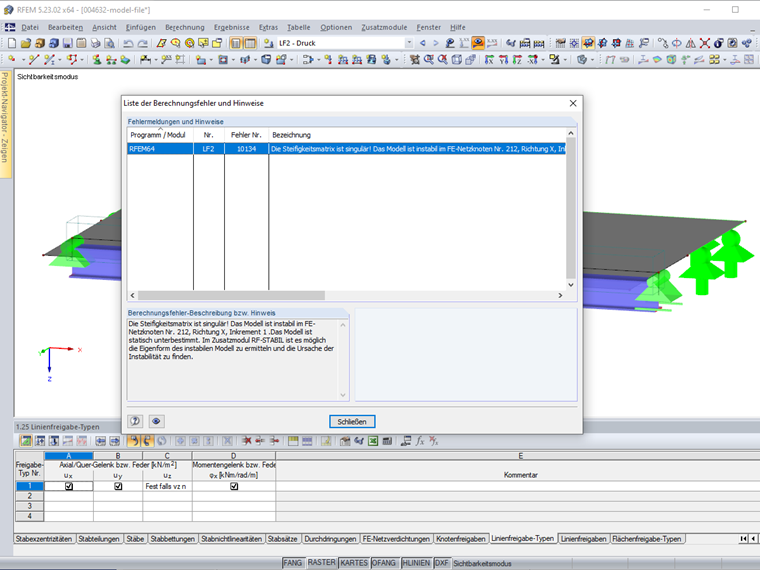
Bei einer Berechnung wird die im Bild 7 dargestellte Instabilitätsmeldung ausgegeben, da die Stäbe ungelagert sind.
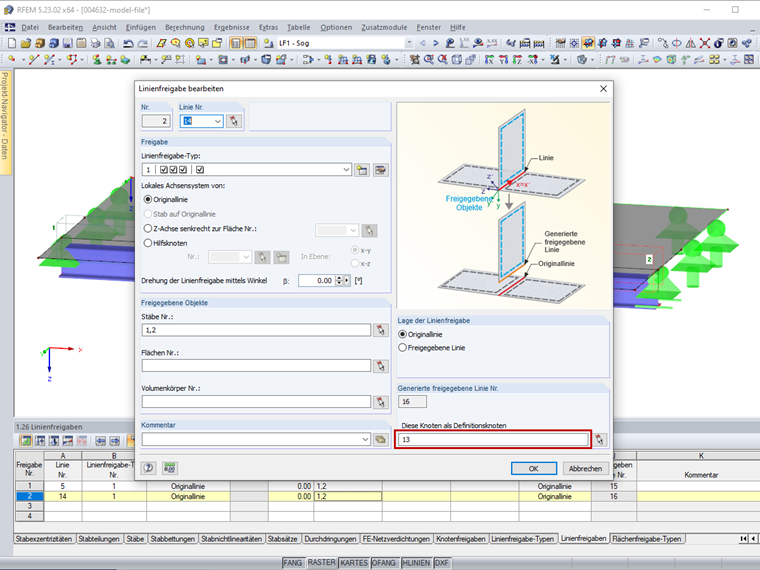
Die Verbindung der Stäbe 1 und 2 kann hergestellt werden, indem in der Linienfreigabe 2 der von der Linienfreigabe 1 generierte Knoten 13 als Definitionsknoten definiert wird (Bild 8). Die Stäbe 1 und 2 teilen sich dann denselben Knoten 13 und sind damit verbunden.
Des Weiteren sind die Knotenlager 1 und 2 an den Knoten der Stäbe 1 und 2 zu definieren (Bild 9).