Назад к руководствам онлайн

7660x

000076

Dipl.-Ing. Франк Фаулстих

2023-12-14

Выбрать руководство

Обзор

Графический интерфейс пользователя и настройки

Центр Dlubal

основные данные о модели

Конструкция

Несовершенства

Загружения и сочетания нагрузок

Мастера нагрузок

Нагрузки

Результирующие объекты

raschet

Результат

Вспомогательные объекты

Функции программы

Анализ результатов

Протокол результатов

Нелинейная работа материалов

Материальные модели

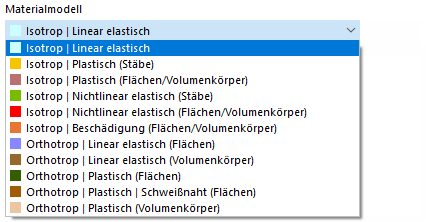
Если в Основные данные модели активирован дополнительный анализ Пластическое материалповедение (требуется лицензия), в списке материалов доступны дополнительные варианты помимо моделей 'Изотропный | Линейный упругий' и 'Ортотропный | Линейный упругий'.

Модели материалов для аддона анализа "Нелинейное поведение материалов"

Модели материалов для аддона Анализ нелинейных материалов

Методики расчетов

При использовании нелинейной модели материала всегда выполняется итеративный расчет. В зависимости от модели материала определяется различная зависимость между напряжением и деформацией.

Жесткость конечных элементов корректируется в ходе итераций до выполнения закономерности напряжение-деформация. Корректировка проводится всегда для целого поверхностного или объемного элемента. При оценке напряжений следует использовать тип сглаживания Константный в элементах сети.

Сглаживание результатов

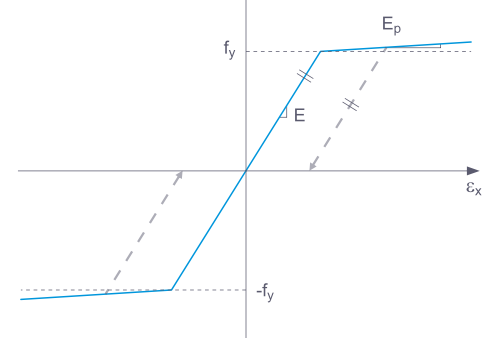
Некоторые модели материала в RFEM обозначены как 'пластические', другие - как 'нелинейно упругие'. Если снята нагрузка с нелинейно упругого материала, деформация возвращается по тому же пути. При полном снятии нагрузки не остается остаточной деформации.

Диаграмма напряжение-деформация, нелинейно-упругая

При снятии нагрузки с компонента с пластической моделью материала после полного снятия нагрузки остается остаточная деформация.

Диаграмма напряжение-деформация, пластическая

Нагрузка и разгрузка могут быть смоделированы с помощью аддона софт-rfem/аддоны-для-rfem-6/дополнительная-аналез/анализ-состояний-зданий Анализ строительных условий.

Фоновая информация о нелинейных моделях материала доступна в статье Закон упрочнения для изотропной нелинейной упругости.

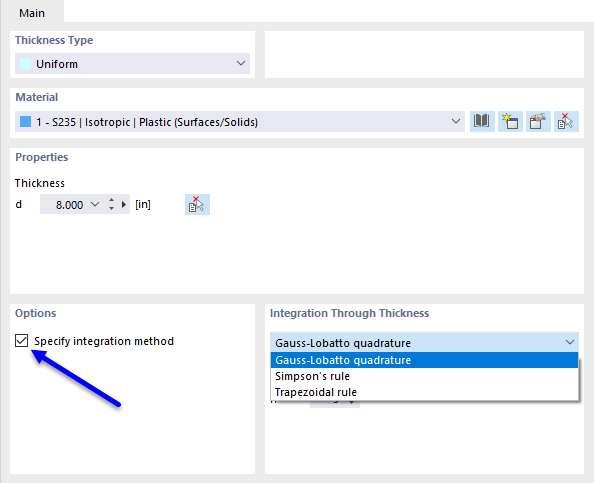
Внутренние усилия в пластинах с нелинейным материалом получаются в результате численной интеграции напряжений по толщине пластины. Чтобы установить метод интеграции по толщине, в диалоге 'Редактировать толщину' отметьте флажок Указать метод интеграции. Предлагаются следующие методы интеграции:

Гаусс-Лобатто-Квадратура
Правило Симпсона
Правило Трапеции

Определить метод интегрирования для толщины поверхности

Кроме того, вы можете задать 'Число точек интеграции' по толщине пластины от 3 до 99.

Инфо

Теоретическое объяснение отдельных методов интеграции приведено в руководстве Многослойные поверхности.

Изотропный пластический (стержни)

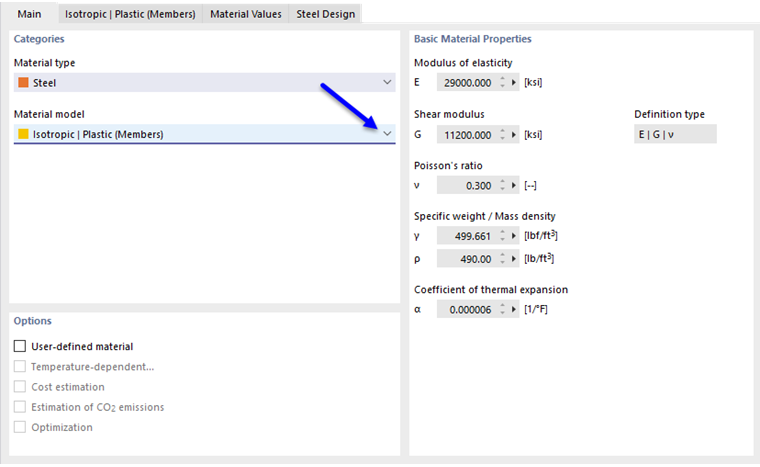
Если в выпадающем списке 'Модель материала' выбрать пункт Изотропный | Пластический (Стержни), активируется вкладка для ввода нелинейных параметров материала.

Активация нелинейной модели материала

Определение нелинейных параметров материала

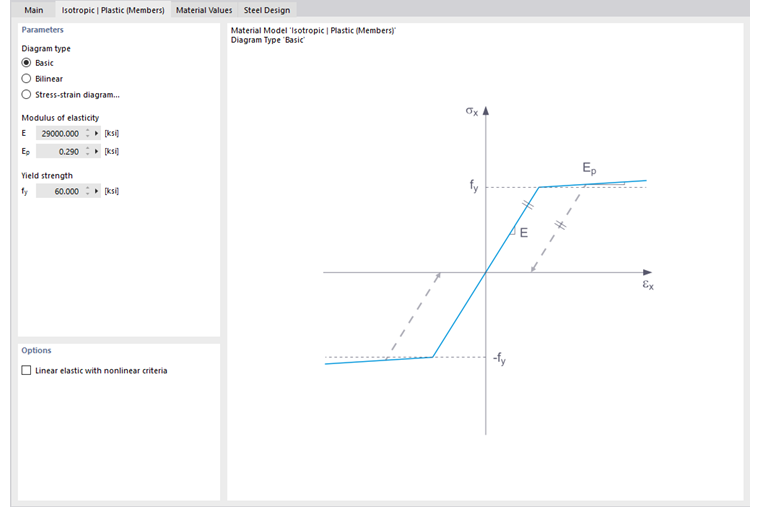
В этой вкладке вы определяете диаграмму напряжение-деформация. Вы можете выбрать следующие варианты:

Стандартный
Билинейный
Диаграмма

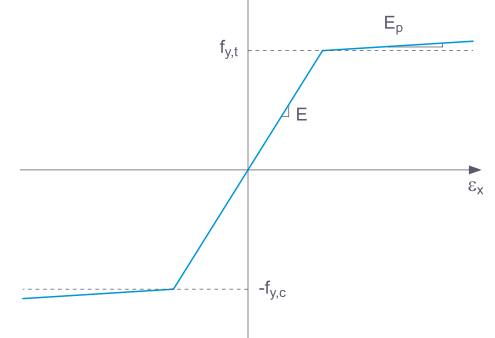
Если выбран Стандартный, то RFEM использует билинейную модель материала. Значения для модуля упругости E и предела текучести f_y берутся из базы данных материалов. По численным причинам, ветвь не горизонтальна, а имеет небольшой наклон E_p.

Если вы хотите изменить значения предела текучести и модуля упругости, отметьте в вкладке 'Базовый' контрольное поле Пользовательский материал.

Активировать пользовательский материал

При билинейном определении вы также можете ввести значение для E_p.

Более сложные зависимости между напряжением и деформацией вы определяете с помощью диаграммы напряжение-деформация. Если вы выберете эту опцию, появится вкладка 'Диаграмма напряжение-деформация'.

Ввод пользовательской диаграммы напряжение-деформация

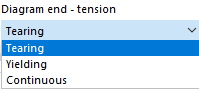
Определите в каждой строке точку для зависимости напряжение-деформация. Как диаграмма должна продолжаться после последней точки определения, можно выбрать в списке 'Конец диаграммы' под диаграммой:

Плавный переход от последней точки определения

Переход после последней точки определения

При 'Разрыве' напряжение после последней точки определения возвращается к нулю. 'Течение' означает, что напряжение при увеличении деформации остается постоянным. 'Непрерывно' означает, что кривая продолжается с наклоном последнего сегмента.

Инфо

В этой модели материала диаграмма напряжение-деформация относится к продольному напряжению σ_x. Разные пределы текучести для растяжения и сжатия с этой моделью материала учесть нельзя.

Изотропный нелинейно упругий (Поверхности/Объемные элементы)

Если в выпадающем списке 'Модель материала' выбрать пункт Изотропный | Пластический (Поверхности/Объемные элементы), активируется вкладка для ввода нелинейных параметров материала.

Выберите модель пластического материала

Сначала выберите 'Гипотезу разрушения по напряжениям'. Выбор предложенных гипотез:

Мизеса (Гипотеза энергии изменения формы)
Треска (Гипотеза касательных напряжений)
Друкер-Прагера
Мора-Кулона

Определение гипотезы разрушения при напряжении

Если вы выберете по Мизесу, в диаграмме напряжение-деформация используются следующие напряжения:

Поверхности

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

Эквивалентное напряжение из основных напряжений по фон Мизесу

Объемные элементы

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Эквивалентное напряжение σ_{v, Мизес} от основных напряжений

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Эквивалентное напряжение σ_{v, Мизес} от главных напряжений

Согласно гипотезе Треска используются следующие напряжения:

Поверхности

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

Эквивалентное напряжение по Треске

Объемные элементы

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Эквивалентное напряжение σ_{v, Tresca}

Согласно гипотезе Друкер-Прагера используется это напряжение для поверхностей и объемов:

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	Пограничное напряжение для сжатия
σ_t	Предел прочности при растяжении

Критерий текучести по Друкеру-Прагеру

Согласно гипотезе Мора-Кулона для поверхностей и объемов используются следующие напряжения:

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

Мор - Кулон

Изотропный нелинейно упругий (Стержни)

Функционал аналогичен модели материала Изотропный пластический (Стержни), но, в отличие от него, после разгрузки не остается пластической деформации.

Изотропный нелинейно упругий (Поверхности/Объемные элементы)

Функционал аналогичен модели материала Изотропный пластический (Поверхности/Объемные элементы), но, в отличие от него, после разгрузки не остается пластической деформации.

Изотропное повреждение (Поверхности/Объемные элементы)

В отличие от других моделей материала, диаграмма напряжение-деформация для этой модели материала не симметрична относительно начала координат. Таким образом, на этой модели материала можно, например, представить поведение бетона с фибровым армированием. Подробные инструкции по моделированию бетона с фибровым армированием вы можете найти в статье Свойства материалов для бетона с фибровым армированием.

Модель материала «Изотропная | Ущерб »

Изотропная жесткость уменьшается с использованием скалярного параметра повреждения. Этот параметр повреждения определяет зависимость от хода напряжений, установленного в диаграмме. При этом не учитывается направление главных напряжений, а повреждение происходит в направлении эквивалентной деформации, которая также затрагивает третье направление, перпендикулярное к плоскости. Зоны натяжения и сжатия в тензоре напряжений обрабатываются отдельно. Для каждого случая применяются различные параметры повреждения.

'Размер референтного элемента' управляет тем, как деформация в зоне трещины масштабируется по длине элемента. При установленном по умолчанию значении ноль, масштабирование не выполняется. Это позволяет реалистично моделировать материалповедение бетона с фибровым армированием.

Теоретические основы материала 'Изотропное повреждение' изложены в статье Нелинейное моделирование повреждений.

Ортотропный пластический (Поверхности) / Ортотропный пластический (Объемные элементы)

Модель материала по Цай-Ву сочетает в себе пластические и ортотропные свойства. Это позволяет выполнять специфическое моделирование материалов с анизотропной характеристикой, таких как армированные волокном пластики или дерево.

При пластической деформации материала напряжения остаются постоянными. Происходит перераспределение в зависимости от жесткостей, которые присутствуют по отдельным направлениям.

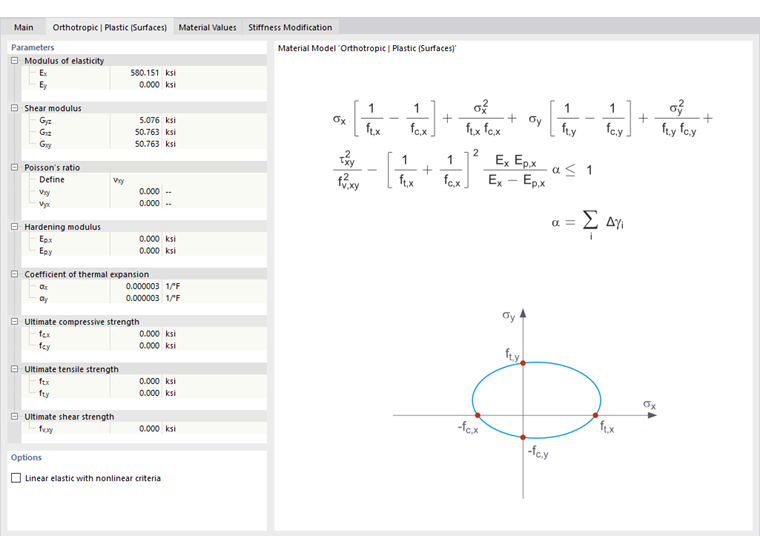
Модель материала «Ортотропная | Пластик (поверхности) »

Модель материала ' ортотропная | Пластик (сплошной) '

Упругий диапазон соответствует модели материала Ортотропный линейный упругий (Объемные элементы). Для пластического диапазона применяется следующее условие текучести по Цай-Ву:

Поверхности

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

\frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} - {[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Цай-Ву, Планарное напряженное состояние

Объемные элементы

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

σ_{z} [\frac{1}{f_{t, z}} - \frac{1}{f_{c, z}}] + \frac{{σ_{z}}^{2}}{f_{t, z} f_{c, z}} +

\frac{{τ_{yz}}^{2}}{{f_{v, yz}}^{2}} + \frac{{τ_{xz}}^{2}}{{f_{v, xz}}^{2}} + \frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} -

{[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Цай-Ву, Пространственное напряжение

Все устойчивости должны задаваться как положительные.

Условие текучести можно представить в виде эллипсоидной поверхности в шестиосном пространстве напряжений. Если одну из трех компонентов напряжения принять постоянной, поверхность можно проецировать на трехмерное напряженно-пространство.

Если значение для f_y(σ) по уравнению Tsai-Wu, плоское напряженное состояние меньше единицы, напряжение находится в упругом диапазоне. Пластический диапазон достигается, как только f_y(σ) = 1. Значения больше единицы недопустимы. Модель ведет себя идеально-пластически, то есть упрочнение отсутствует.

Ортотропный пластический сварной шов (Поверхности)

Эта модель материала используется в анализах с добавлением аддона софт-rfem/аддоны-для-rfem-6/соединения/сталесоединения/сталесоединения-ввод Стальные соединения для адекватного отображения поведения сварных швов в соответствии с нормами. В замещающей поверхности возникают только напряжения, соответствующие компонентам напряжений σ_⊥, τ_⊥ и τ_|| сварного шва. В остальном направлениях напряжений жесткость замещающей поверхности стремится к нулю.

Модель материала “Ортороп | Пластический | Сварной шов (поверхности)”

Модель материала «Ортотропный | Пластический | Сварной шов (поверхности)»

На вкладке 'Ортотропный | Пластический | Сварной шов (Поверхности)' можно настроить параметры для учета пластического упрочнения материала в сварных швах, такие как предельные значения f_ekv и f_x для проверки напряжений по "направленному методу" согласно EN 1993-1-8 [1] для сварных швов, модифицированного на долю пластичности (см. также статью Проверка сварных швов).

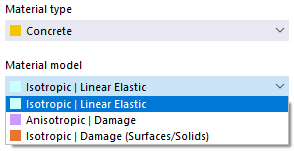
Бетон

Для типа материала 'Бетон' доступны нелинейные модели материала 'Анизотропное | Повреждение' и 'Изотропное | Повреждение (Поверхности/Объемные элементы)'.

Модели материалов для бетона

Эти модели материала описаны в главе Анизотропное | Повреждение руководства по бетону или в разделе Изотропное повреждение выше.

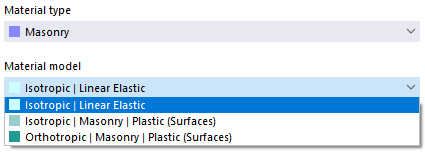
Кирпичная кладка

Если в Основные данные модели активирован аддон расчета Расчет кирпичной кладки (требуется лицензия), для типа материала 'Кирпичная кладка' доступны нелинейные модели материалов 'Изотропная | Кирпичная кладка | Пластическая (Поверхности)' и 'Ортотропная | Кирпичная кладка | Пластическая (Поверхности)'.

Модели материалов для кладки

Обе модели материала описаны в главе Материалы руководства по кирпичной кладке.

Ссылки

Европейский комитет по стандартизации. (2009). Еврокод 3: Расчет стальных конструкций. Часть 1-8: Bemessung von Anschlüssen. Beuth Verlag GmbH, Berlin, 2010

Исходная глава

Материалы

Модели

1343x

120x

Материальный нелинейный расчёт

709x

45x

Модель материала Цай-Ву | Ортотропная упруго-пластичная

1338x

113x

Угловое соединение рамы