用户使用手册 RFEM 6

返回在线手册

7688x

000076

Dipl.-Ing.弗兰克·福尔施蒂奇

2023-12-14

选择手册

概览

图形用户界面和设置

Dlubal 中心

模型 - 基本数据

结构

缺陷

荷载工况和组合

荷载向导

荷载

结构对象

计算

结果

辅助对象

程序功能

结果评估

计算书

材料的非线性行为

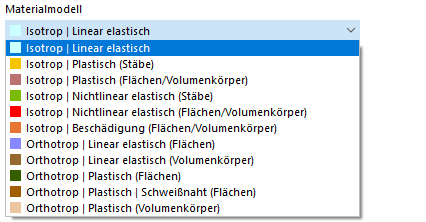
材料模型

如果在 Modell-Basisangaben 中启用了分析附加组件非线性材料行为 (需要许可证)，除了材料模型 '各向同性 | 线性弹性' 和 '正交各向异性 | 线性弹性' 之外，材料模型列表中还有其他选项可供选择。

“非线性材料行为”分析模块材料模型

计算方法

如果您使用非线性材料模型，将始终执行迭代计算。根据材料模型的不同，会定义不同的应力与应变之间的关系。

有限元的刚度在迭代过程中不断调整，直到满足应力-应变关系。调整总是针对整个表面或体积单元进行。因此，在评估应力时，始终应使用平滑类型恒定在网格元素内。

结果平滑

在 RFEM 中，一些材料模型称为 '塑性'，另一些则称为 '非线性弹性'。如果用 非线性弹性 材料的构件卸载，变形沿同一路径返回。完全卸载后，无变形残留。

应力-应变图，非线性弹性

用塑性材料模型的构件卸载后，完全卸载后会残留变形。

应力-应变图，塑性

加载和卸载可以通过附加组件建筑状态分析模拟。

有关非线性材料模型的背景信息，请参阅技术文章等向非线性弹性材料模型的流变法则。

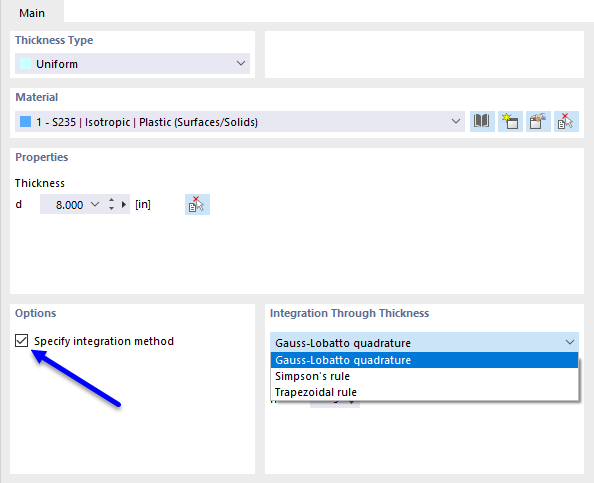
板材中非线性材料的内力是通过板厚度的应力数值积分得出的。要设置厚度的积分方法，请在 '编辑厚度' 对话框中勾选选项 指定积分方法。可选择的积分方法如下：

高斯-罗巴托数值积分
辛普森法则
梯形法则

定义面厚度的积分方法

此外，您可以在板厚度范围内从 3 到 99 指定 '积分点的数量'。

信息

关于各个积分方法的理论解释，请参阅手册多层表面。

各向同性塑性 (杆件)

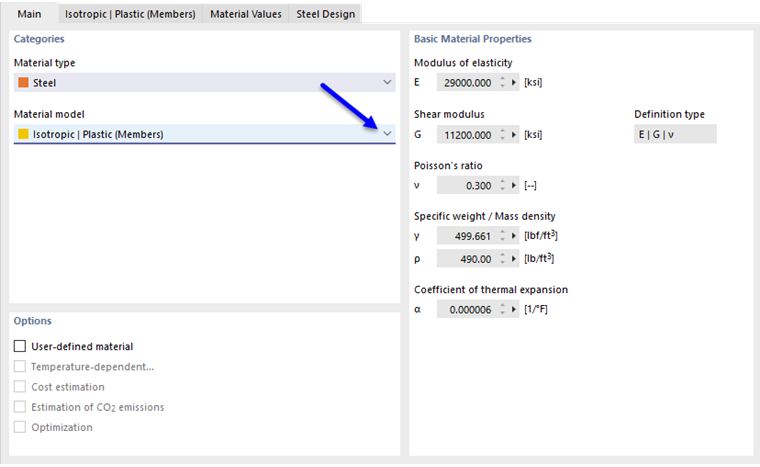
如果在 '材料模型' 下拉列表中选择 各向同性 | 塑性 (杆件)，则将激活输入非线性材料参数的选项卡。

激活非线性材料模型

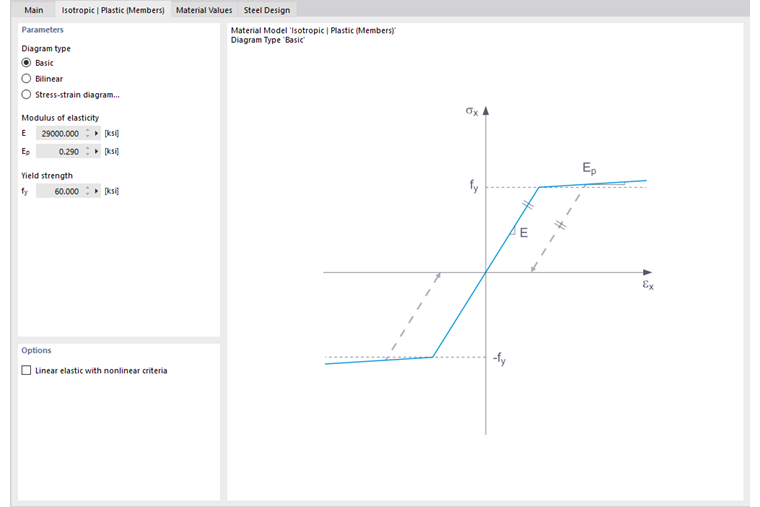
定义非线性材料参数

在此选项卡中，您可以定义应力-应变图。可供选择的选项有：

标准
双线性
图形

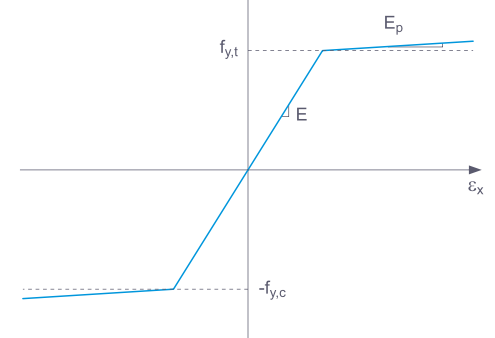
如果选择了标准，RFEM 将使用双线性材料模型。弹性模量 E 和屈服强度 f_y 的值将取自材料数据库。出于数值原因，曲线并非完全水平，而是有一个小的上升 E_p。

如果要更改屈服强度和弹性模量的值，请在 '基本' 选项卡中启用复选框 自定义材料。

激活用户自定义材料

在 双线性 定义中，您也可以输入 E_p 的值。

更复杂的应力与应变关系可以通过 应力-应变图 来定义。如果选择此选项，则将显示 '应力-应变图' 选项卡。

输入用户自定义的应力-应变图

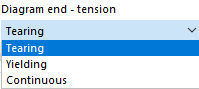
在每一行定义应力-应变关系的一个点。您可以在图的下方的 '图终点' 列表中选择该图在最后定义点后的走向：

最后一个定义点之后的曲线变化

在 '断裂' 情况下，应力在最后一个定义点后回落至零。'流动' 意味着随着应变的增加，应力保持不变。'连续' 意味着曲线继续以最后一段的斜率延伸。

信息

在此材料模型中，应力-应变图指的是纵向应力 σ_x。该材料模型无法考虑不同的拉伸和压缩屈服强度。

各向同性塑性 (面/体)

如果在 '材料模型' 下拉列表中选择 各向同性 | 塑性 (面/体)，则将激活输入非线性材料参数的选项卡。

选择塑性材料模型

首先选择 '应力失效假设'。可选择的假设有：

冯·米塞斯 (形变能假设)
特雷斯卡 (剪应力假设)
德鲁克-普拉格
摩尔-库仑

定义应力破坏假设

如果选择 冯·米塞斯，应力-应变图中将使用以下应力：

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

根据 von Mises 由基本应力计算等效应力

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

根据基本应力计算等效应力 σ_v,Mises

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

由主应力计算的等效应力 σ_v,Mises

根据 特雷斯卡 假设，使用以下应力：

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

根据 Tresca 的等效应力

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

等效应力 σ_v,Tresca

根据 德鲁克-普拉格 假设，面和体使用以下应力：

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	压力极限应力
σ_t	拉应力的极限

Drucker-Prager 屈服准则

根据 摩尔-库仑 假设，面和体使用以下应力：

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

莫尔-库伦

各向同性非线性弹性 (杆件)

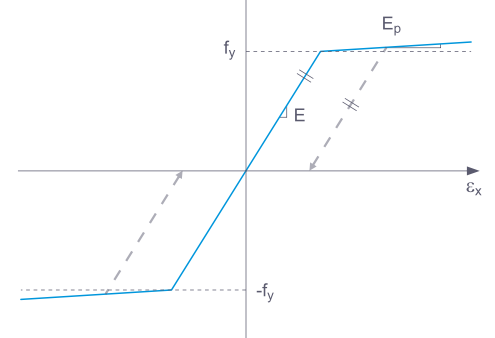
工作方式与材料模型各向同性塑性 (杆件) 大体相同。与之不同的是，卸载后不会残留塑性变形。

各向同性非线性弹性 (面/体)

工作方式与材料模型各向同性塑性 (面/体) 大体相同。与之不同的是，卸载后不会残留塑性变形。

各向同性损伤 (面/体)

与其他材料模型不同，该材料模型的应力-应变图并不关于原点对称。因此，使用此材料模型可以模拟例如钢纤维混凝土的行为。关于钢纤维混凝土建模的详细信息，请参阅技术文章钢纤维混凝土的材料特性。

材料模型“各向同性” | 损伤"

各向同性刚度通过标量损伤参数被减弱。损伤参数由图中定义的应力路径确定，并不考虑主应力的方向，而是损伤发生在拉伸变形的方向，同时第三个方向垂直于平面。应力张量的拉伸和压缩部分被分别处理，分别有不同的损伤参数。

'参考元素尺寸' 控制裂缝区域的变形如何按元素长度缩放。默认值为零，表示不进行缩放。这样可以更真实地反映钢纤维混凝土的材料行为。

关于 '各向同性损伤' 材料模型的理论背景，请参阅技术文章非线性材料模型损伤。

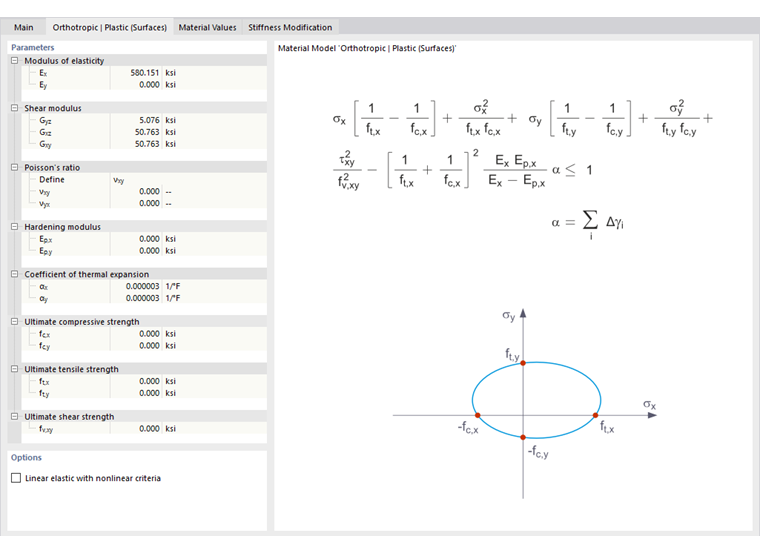
正交各向异性塑性 (面) / 正交各向异性塑性 (体)

根据 "蔡-吴" 材料模型结合了塑性和正交各向异性特性。它允许对具有各向异性特征的材料进行特殊建模，如纤维增强塑料或木材。

材料塑性化后，应力保持不变。相应依据信赖的刚度进行重分布。

材料模型“正交各向异性” | 塑性（面）"

材料模型 ' 正交各向异性 | 塑料（实体）'

弹性区域遵循材料模型正交各向同性线性弹性 (体)。对于塑性区域，依据 "蔡-吴" 公式的流动条件如下：

正交各向异性塑性焊缝 (面)

此材料模型用于分析附加组件钢连接，以规范地模拟焊缝行为。在替代面上，仅产生与焊缝应力分量 σ_⊥、τ_⊥ 和 τ_|| 相应的应力。替代面的其他应力方向的刚度趋于零。

材料模型“正交各向异性 | 塑性 | 焊缝(面)”

在 '正交各向异性 | 塑性 | 焊缝 (面)' 选项卡中，您可以设置考虑焊缝塑性材料硬化的参数，例如焊缝的应力验证极限值 f_ekv 和 f_x 按照 EN 1993-1-8 [1] 的 "方向性方法" 以及经过修改的塑性成分 (详见技术文章角焊缝验证 )。

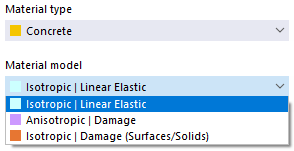
混凝土

对于材料类型 '混凝土'，可选择的非线性材料模型有 '各向异性 | 损伤' 和 '各向同性 | 损伤 (面/体)'。

混凝土的材料模型

这些材料模型在混凝土手册的章节各向异性 | 损伤或在上面各向同性损伤部分中描述。

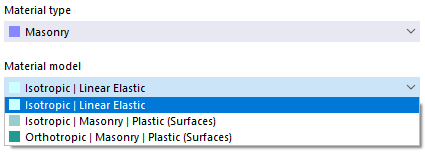
砌体

如果在 Modell-Basisangaben 中启用了设计附加组件砌体设计 (需要许可证)，则对于材料类型 '砌体'，可选择的非线性材料模型有 '各向同性 | 砌体 | 塑性 (面)' 和 '正交各向异性 | 砌体 | 塑性 (面)'。

砌体材料模型

这两种材料模型在砌体手册的章节材料中描述。

参考

欧洲标准化委员会。 (2009)。欧洲规范 3： Bemessung und Konstruktion von Stahlbauten – Teil 1-8: Bemessung von Anschlüssen. Beuth Verlag GmbH, Berlin, 2010

上级章节

材料

模型

1348x

121x

材料非线性分析

710x

46x

Tsai-Wu 材料模型| 正交各向异性弹塑性

1344x

113x

框架节点