Zpět k online manuálům

7550x

000076

Dipl.-Ing. Frank Faulstich

14.12.2023

Vybrat manuál

Přehled

Uživatelské prostředí a nastavení

Dlubal centrum

Základní údaje o modelu

Konstrukce

Imperfekce

Zatěžovací stavy a kombinace

Generátor zatížení

Zatížení

Výsledkové objekty

Výpočet

Výsledky

Pomocné objekty

Funkce programu

Vyhodnocení výsledků

Tiskové protokoly

Nelineární chování materiálu

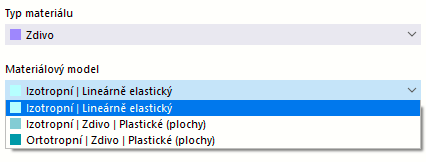
Materiálové modely

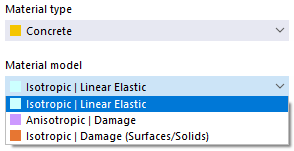
Pokud je v Modelové základní údaje aktivováno add-on Nelineární materiálové chování (vyžadována licence), jsou kromě materiálových modelů 'Izotropní | Lineárně elastický' a 'Ortropní | Lineárně elastický' v seznamu materiálových modelů k dispozici další možnosti.

Materiálové modely pro addon Nelineární chování materiálu

Výpočetní metody

Pokud používáte nelineární materiálový model, vždy se provádí iterativní výpočet. V závislosti na materiálovém modelu se definuje jiný vztah mezi napětími a deformacemi.

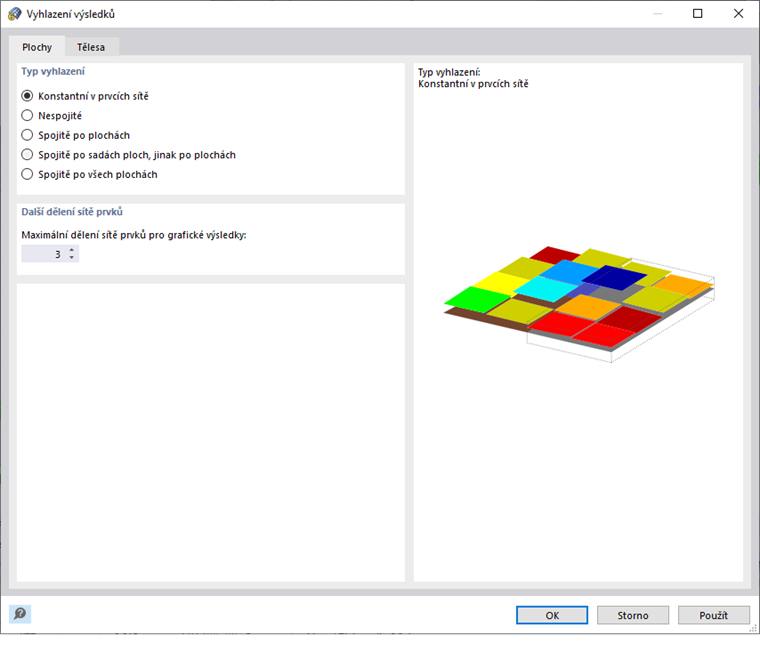
Tuhost prvků konečných elementů se v průběhu iterací neustále přizpůsobuje, dokud není dodržen vztah napětí-deformace. Přizpůsobení se provádí vždy pro celý plošný nebo objemový prvek. Při vyhodnocování napětí by proto měla být vždy použita metoda vyhlazení Konstanta v síťových prvcích.

Vyhlazení výsledků

Některé materiálové modely v RFEMu jsou označeny jako 'plastické', jiné jako 'nelineárně elastické'. Pokud je prvek s nelineárně elastickým materiálem uvolněn, vrací se deformace po stejné cestě zpět. Po úplném uvolnění nezůstává žádná deformace.

Pracovní diagram, nelineárně elastický

Při uvolnění prvku s plastickým materiálovým modelem zůstává po úplném uvolnění deformace.

Pracovní diagram, plastický

Zatížení a odlehčení lze simulovat pomocí add-onu Analýza stavebních stavů.

Informace na pozadí o nelineárních materiálových modelech naleznete v odborném článku Tokové zákony v materiálovém modelu Izotropní nelineárně elastický.

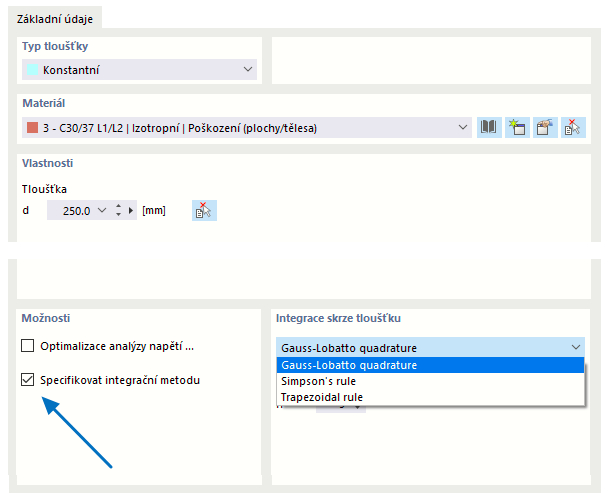
Vnitřní síly v deskách s nelineárním materiálem vznikají z numerické integrace napětí přes tloušťku desky. Pro stanovení integrační metody pro tloušťku zatrhněte v dialogu 'Upravit tloušťku' volbu Zadat integrační metodu. Poté jsou k dispozici následující integrační metody pro výběr:

Gauss-Lobatto kvadratura
Simpsonovo pravidlo
Trapezové pravidlo

Zadat integrační metodu pro tloušťku plochy

Dále můžete stanovit 'Počet integračních bodů' přes tloušťku desky od 3 do 99.

Informace

Teoretické vysvětlení jednotlivých integračních metod najdete v příručce Vícevrstvé plochy.

Izotropní plastický (Pruty)

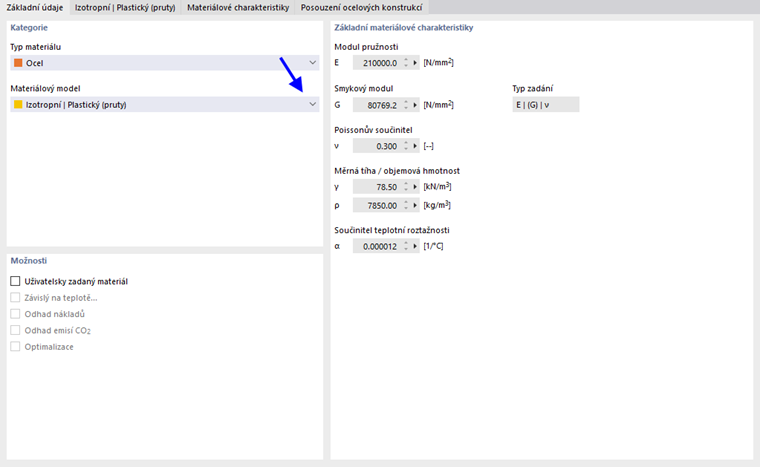
Pokud v rozbalovacím seznamu 'Materiálový model' vyberete položku Izotropní | Plastický (Pruty), pak se otevře záložka pro zadání nelineárních materiálových parametrů.

Aktivujte nelineární materiálový model

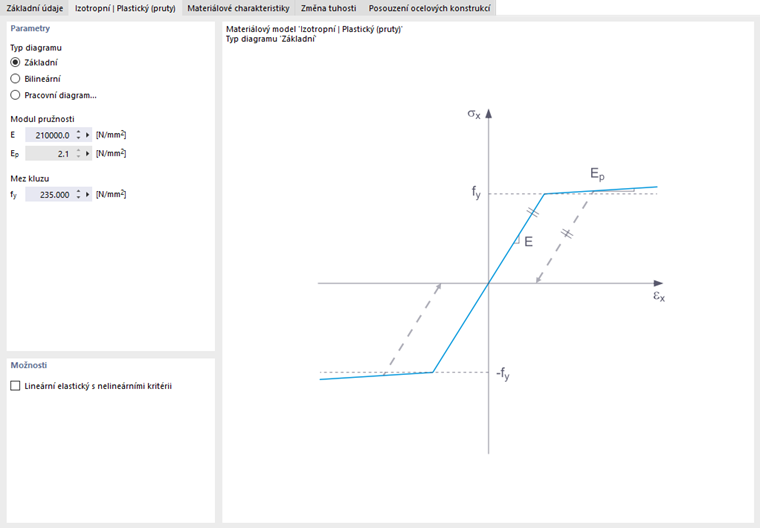
Definujte nelineární parametry materiálu

V této záložce definujete diagram napětí-deformace. Pro tento účel jsou k dispozici následující možnosti:

Standard
Bilineární
Diagram

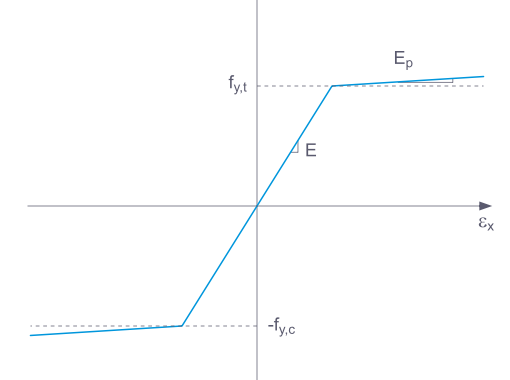
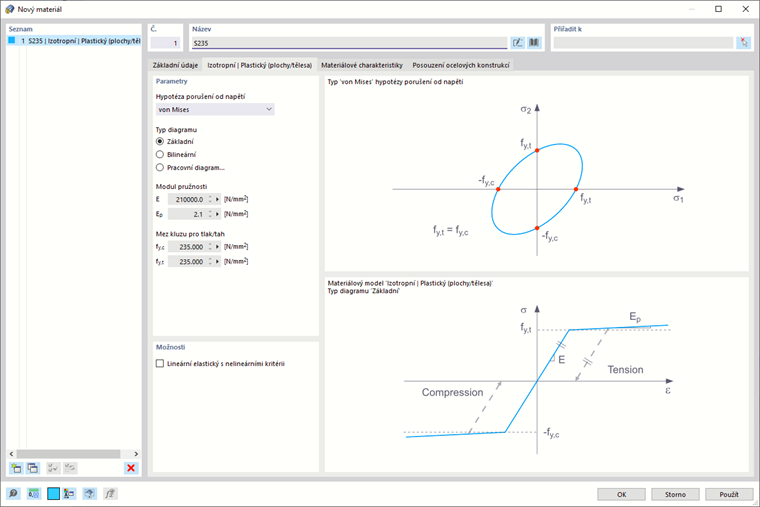
Pokud je vybrána možnost Standard, pak RFEM používá bilineární materiálový model. Hodnoty modulu pružnosti E a mez kluzu f_y se používají z materiálové databáze. Z numerických důvodů není průběh přesně horizontální, ale má malý vzrost E_p.

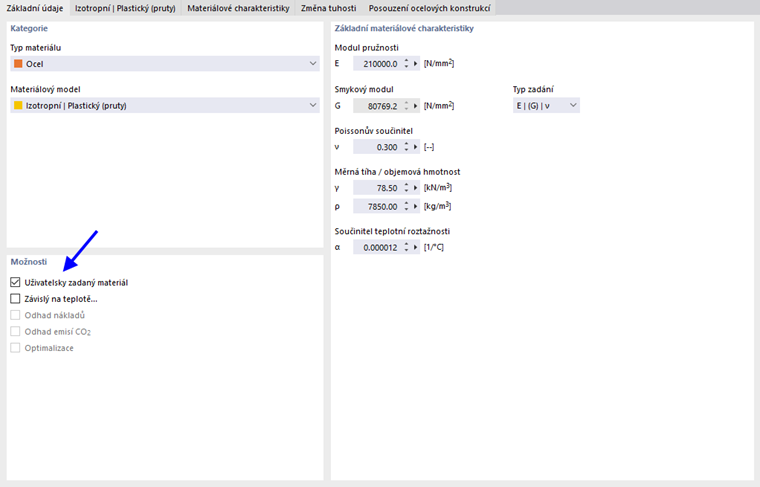
Pokud chcete změnit hodnoty pro mez kluzu a modul pružnosti, aktivujte v záložce 'Základ' pole Vlastní materiál.

Aktivovat uživatelsky definovaný materiál

Při bilineární definici můžete také zadat hodnotu pro E_p.

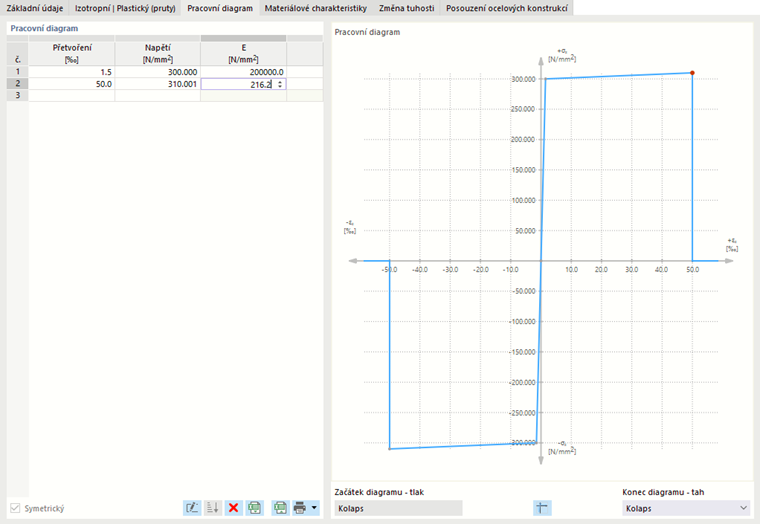
Složitější vztahy mezi napětím a deformací definujete pomocí Diagramu napětí-deformace. Pokud tuto možnost vyberete, pak se zobrazí záložka 'Diagram napětí-deformace'.

Zadejte uživatelsky definovaný pracovní diagram

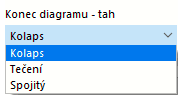
V každém řádku definujte bod pro vztah napětí-deformace. Jak má být diagram rozšířen za poslední definiční bod, si můžete zvolit v seznamu 'Konec diagramu' pod diagramem:

Pokračování za posledním definičním bodem

Při 'Přetržení' napětí po posledním definičním bodě skáče zpět na nulu. 'Plastický průtok' znamená, že napětí při rostoucí deformaci zůstává konstantní. 'Kontinuálně' znamená, že křivka pokračuje se stoupáním posledního úseku.

Informace

U tohoto materiálového modelu se diagram napětí-deformace vztahuje na osové napětí σ_x. Různé meze kluzu pro tah a tlak nelze s tímto materiálovým modelem zohlednit.

Izotropní plastický (Plochy/Objemy)

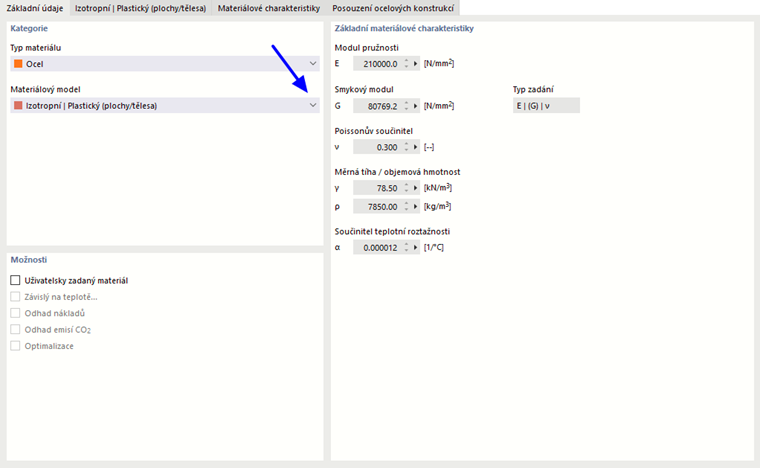
Pokud v rozbalovacím seznamu 'Materiálový model' vyberete položku Izotropní | Plastický (Plochy/Objemy), pak se otevře záložka pro zadání nelineárních materiálových parametrů.

Výběr plastického materiálového modelu

Nejprve vyberte 'Hypotézu selhání napětí'. K dispozici jsou tyto hypotézy:

Von Mises (Hypotéza tvarové změny energie)
Tresca (Hypotéza smykového napětí)
Drucker-Prager
Mohr-Coulomb

Definujte hypotézu selhání napětí

Pokud vyberete možnost Von Mises, použijí se napětí v diagramu napětí-deformace:

Plochy

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

Srovnávací napětí ze základních napětí podle von Misese

Objemové prvky

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Srovnávací napětí σ_{v, Mises} ze základních napětí

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Srovnávací napětí σ_{v, Mises} z hlavních napětí

Podle hypotézy Tresca se použijí tato napětí:

Plochy

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

Srovnávací napětí podle Trescy

Objemové prvky

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Srovnávací napětí σ_{v, Tresca}

Podle hypotézy Drucker-Prager se pro plochy a objemy použije následující napětí:

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	Mezní napětí pro tlak
σ_t	Mezní napětí pro tah

Výnosové kritérium podle Drucker-Prager

Podle hypotézy Mohr-Coulomb se pro plochy a objemy použije následující napětí:

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

Mohr - Coulomb

Izotropní nelineárně elastický (Pruty)

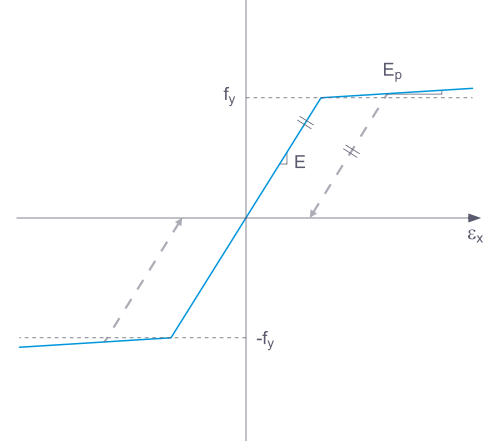
Funkce je téměř stejná jako u materiálového modelu Izotropní plastický (Pruty). Na rozdíl od tohoto modelu však po uvolnění nezůstává žádná plastická deformace.

Izotropní nelineárně elastický (Plochy/Objemové prvky)

Funkce je podobná jako u materiálového modelu Izotropní plastický (Plochy/Objemy). Na rozdíl od tohoto modelu však po uvolnění nezůstává žádná plastická deformace.

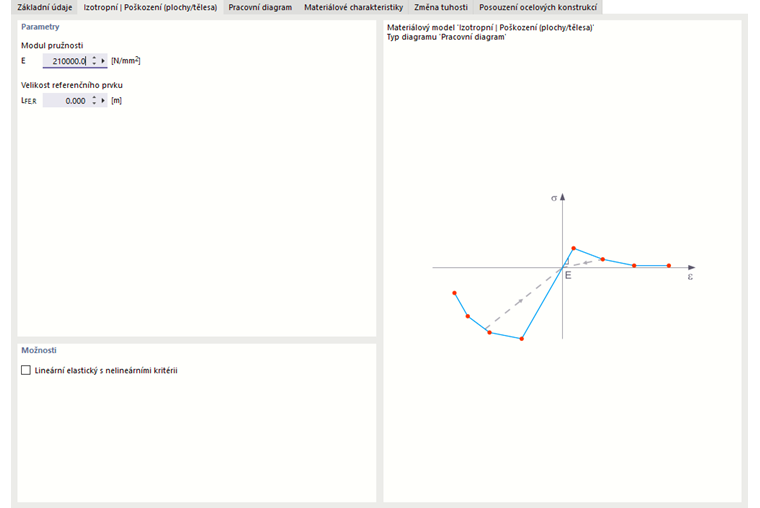
Izotropní poškození (Plochy/Objemové prvky)

Na rozdíl od jiných materiálových modelů není diagram napětí-deformace pro tento materiálový model antisymetrický vzhledem k počátku. Takže je tímto materiálovým modelem možné například modelovat chování ocelovláknobetonu. Podrobné informace o modelování ocelovláknobetonu naleznete v odborném článku Materiálové vlastnosti ocelovláknobetonu.

Materiálový model "Izotropní | Poškození "

Izotropní tuhost je snížena skalárním poškozovacím parametrem. Tento poškozovací parametr se určuje na základě průběhu napětí, které je stanoveno v diagramu. Nezohledňuje se však směr hlavních napětí, nýbrž poškození probíhá spíše ve směru ekvivalentní deformace, která zahrnuje také třetí směr kolmo na rovinu. Napěťový a tlakový rozsah napěťového tenzoru se ošetřuje samostatně. Pro každý platí jiné poškozovací parametry.

'Referenční velikost prvku' určuje, jak je deformace v trhlinové oblasti škálována na délku prvku. Při přednastavené hodnotě nula nedochází k žádné škálování. Tím se reálně zobrazuje materiálové chování ocelovláknobetonu.

Teoretické pozadí materiálového modelu 'Izotropní poškození' naleznete v odborném článku Nelineární materiálový model poškození.

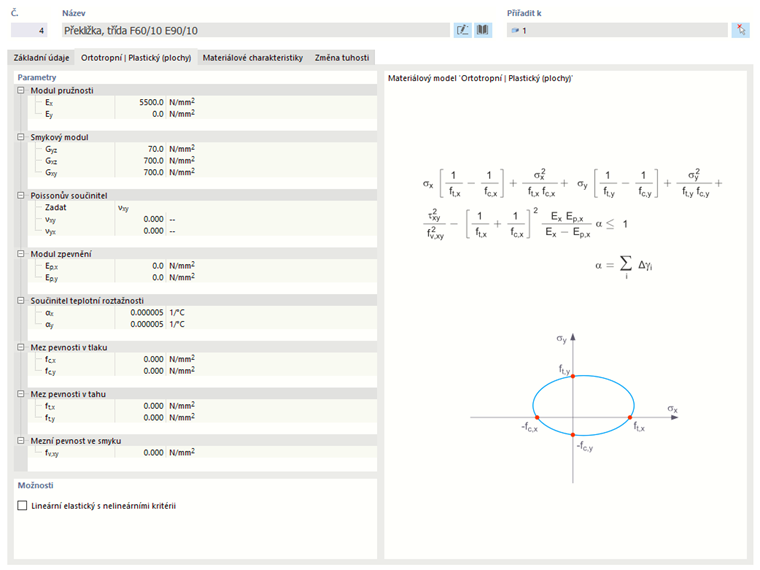
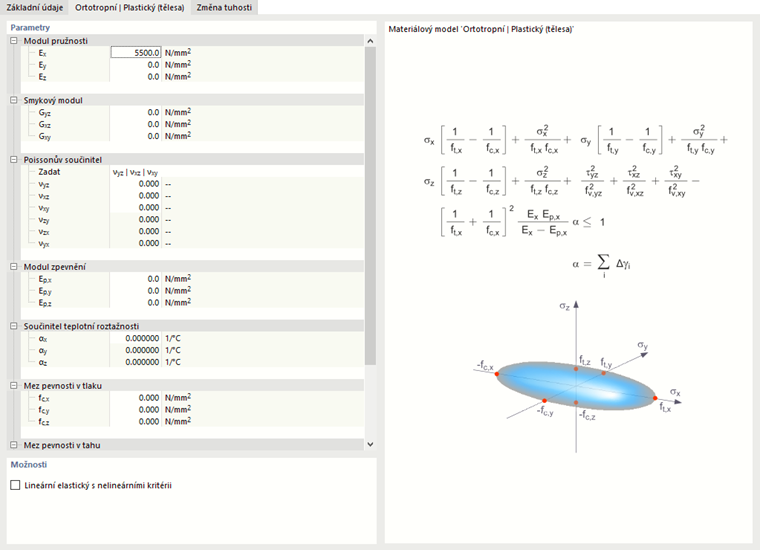
Ortropní plastický (Plochy) / Ortropní plastický (Objemy)

Materiálový model podle Tsai-Wu kombinuje plastické a ortotropní vlastnosti. To umožňuje speciální modelování materiálů s anizotropním chováním, jako jsou kompozity vyztužené vlákny nebo dřevo.

Při přetížení materiálu zůstávají napětí konstantní a dochází k přerozdělení v závislosti na tuhostech, které jsou v jednotlivých směrech.

Materiálový model "Ortotropní" | Plastika (plochy) "

Materiálový model "Ortotropní" | Plastický (těleso) '

Elastická oblast odpovídá materiálovému modelu Ortropní lineárně elastický (Objemy). Pro plastickou oblast platí následující podmínka toku podle Tsai-Wu:

Plochy

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

\frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} - {[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu, rovinný stav napětí

Objemové prvky

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

σ_{z} [\frac{1}{f_{t, z}} - \frac{1}{f_{c, z}}] + \frac{{σ_{z}}^{2}}{f_{t, z} f_{c, z}} +

\frac{{τ_{yz}}^{2}}{{f_{v, yz}}^{2}} + \frac{{τ_{xz}}^{2}}{{f_{v, xz}}^{2}} + \frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} -

{[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu, prostorový stav napětí

Všechny pevnosti musejí být definovány jako kladné.

Podmínku toku lze představit jako eliptickou plochu v šestirozměrném napěťovém prostoru. Pokud je jedna ze tří komponent napětí stanovena jako konstantní hodnota, může být plocha promítnuta do trojrozměrného napěťového prostoru.

Je-li hodnota pro f_y(σ) podle rovnice Tsai-Wu, rovinný stav napětí menší než 1, pak napětí leží v elastické oblasti. Plastická oblast je dosažena, když f_y(σ) = 1. Hodnoty větší než 1 jsou nepřípustné. Model se chová ideálně-plasticky, což znamená, že nedochází k žádnému zpevnění.

Ortropní plastický svár (Plochy)

Tento materiálový model se používá při analýzách s add-onem Ocelové spoje, aby bylo možné normově modelovat chování svárů. V náhradní ploše vznikají pouze napětí, která odpovídají složkám napětí σ_⊥, τ_⊥ a τ_|| sváru. V ostatních směrech napětí klesá tuhost náhradní plochy na nulu.

Model materiálu „Ortotropní | Plastický | Svar (plocha)“

V záložce 'Ortropní | Plastický | Svár (Plochy)' můžete nastavit parametry pro zohlednění plastického zpevnění materiálu u svárů, například hraniční hodnoty f_ekv a f_x pro ověření napětí podle "postup podle směrnic" dle EN 1993-1-8 [1] pro sváry, modifikované o plastickou složku (viz také odborný článek Ověření svárů).

Beton

Pro materiálový typ 'Beton' jsou k dispozici nelineární materiálové modely 'Anizotropní | Poškození' a 'Izotropní | Poškození (Plochy/Objemy)'.

Materiálové modely pro beton

Oba materiálové modely jsou popsány v kapitole Materiálový typ a materiálový model příručky pro beton nebo výše v části Izotropní poškození.

Zděné konstrukce

Pokud je v Modelové základní údaje aktivováno add-on pro navrhování Zděné konstrukce (vyžadována licence), jsou pro materiálový typ 'Zděné konstrukce' k dispozici nelineární materiálové modely 'Izotropní | Zděné konstrukce | Plastický (Plochy)' a 'Ortropní | Zděné konstrukce | Plastický (Plochy)'.

Materiálové modely pro zdivo

Oba materiálové modely jsou popsány v kapitole Materiály příručky pro zděné konstrukce.

Reference

Evropský výbor pro normalizaci. (2009). Eurokód 3: Navrhování ocelových konstrukcí – Část 1-8: Navrhování styčníků; ČSN EN 1993-1-8:2006-12 Beuth Verlag GmbH, Berlin, 2010

Nadřazená kapitola

Materiály

Modely

1332x

119x

Nelineární analýza materiálů

703x

45x

Materiálový model Tsai-Wu | Ortotropní elasticko-plastický

1333x

113x

Rámový přípoj