TS upravené podle Quast a Quast

Quast

Tento model k evidenci spolupůsobení betonu během tahu mezi trhlinami je založen na definovaném pracovním diagramu betonu v tahu (parabolicko-rektangulární pracovní diagram).

Základní předpoklady Quastova přístupu lze shrnout následovně:

• plný příspěvek betonu k tahu až do dosažení přetvoření na trhliny ε_cr nebo výpočtové pevnosti betonu v tahu f_ct,R
• Redukovaný příspěvek zpevnění betonu v tažené oblasti podle stávajícího přetvoření betonu.
• Žádné tahové zpevnění poté, co rozhodující výztužný prut začne povolovat.

V souhrnu to znamená, že pevnost v tahu f_ct,R použitá pro výpočet není pevná hodnota, ale vztahuje se na existující přetvoření v rozhodujícím ocelovém (tahovém) vlákně. Maximální pevnost v tahu f_ct,R lineárně klesá k nule od definovaného přetvoření na trhliny ε_cr až do dosažení přetvoření výztužné oceli v rozhodujícím ocelovém vláknu.
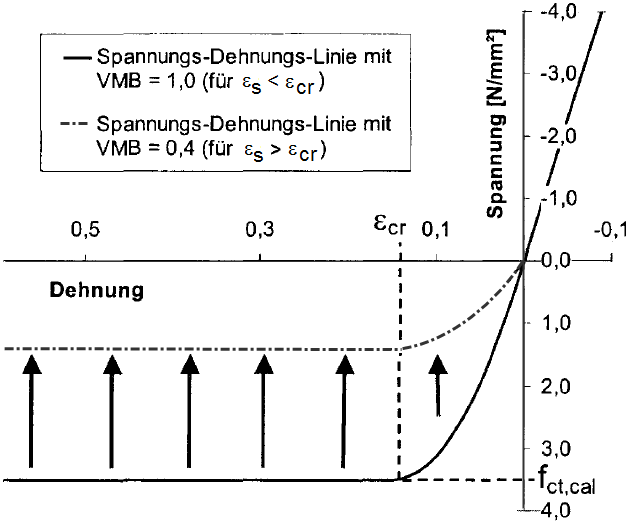
Toho lze dosáhnout pomocí diagramu napětí-přetvoření v tažené oblasti betonu (parabolický obdélníkový diagram) znázorněného na následujícím obrázku a stanovením redukčního součinitele VMB (příspěvek zpevnění betonu).

Napětí-deformace betonu v tahové oblasti s redukčním faktorem VMB = 0,4

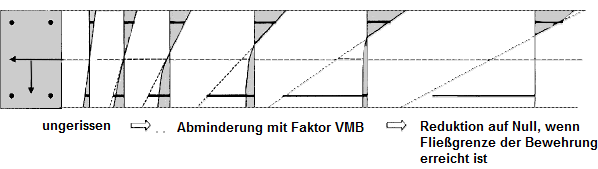
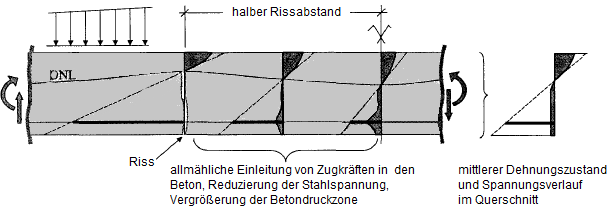
Na následujícím obrázku jsou schematicky znázorněny napěťové stavy při zvyšujícím se zatížení vlivem tahového zpevnění.

Napěťové stavy pro rostoucí zatížení s tahovým vyztužením

Pracovní diagram v tahové oblasti lze popsat pomocí následujících rovnic:

• Zakřivení paraboly v prvním řezu lze řídit pomocí exponentu n_PR.
• Exponent by měl být nastaven tak, aby byl přechod z tlačené oblasti do tažené oblasti přednostně dosažen se stejným modulem pružnosti.

Pro stanovení redukčního součinitele VMB se použije přetvoření na nejvíce namáhaném ocelovém vlákně. Poloha referenčního bodu je znázorněna v následujícím obrázku.

Stanovení zbytkové pevnosti v tahu pro tahové vyztužení podle Quasta

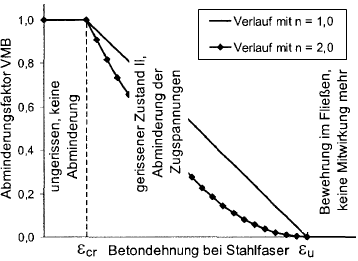
Redukční parametr VMB klesá s rostoucím přetvořením oceli. Z diagramu pro součinitel VMB (viz obrázek níže) je zřejmé, že součinitel VMB je redukován na nulu přesně v bodě, kdy začíná tečení výztuže.

Redukční fakotr VMB – tahové ztužení podle Quasta

Rozdělení pro redukční součinitel VMB ve stavu II (ε > ε_cr ) lze řídit pomocí exponentu n_VMB.

• Podle Pfeiffera[2] jsou hodnoty n_VMB = 1 (lineární) až n_VMB = 2 (parabola) pro konstrukční prvky namáhané ohybem zkušenosti.
• Quast [3] používá ve svém modelu exponent n_VMB = 1 (lineární), čímž dosahuje dobré shody při přepočítání sloupových testů.
• Podle Pfeiffera [2] lze čisté tahové zkoušky popsat s přijatelnou shodou pomocí n_VMB = 2.

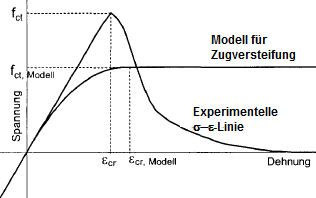
Jako pomůcku při výpočtu lze použít parabolický obdélníkový diagram pro tahovou oblast betonu s trhlinami. Na první pohled jsou vidět velké rozdíly ve srovnání s experimentálně stanovenými pracovními diagramy na tažené straně čistého betonu.

Tahové ztužení podle Quasta - porovnání modelu a laboratorní zkoušky

Daná napětí v železobetonovém průřezu v ohybu ukazují, že parabolický obdélníkový diagram je skutečně vhodnější pro popis střední hodnoty přetvoření a napětí.
V ohýbaném nosníku se mezi dvěma trhlinami vytvoří betonové těleso. Působí jako stěna, do které se postupně znovu vnášejí tahové síly výztuží. Výsledkem je velmi nepravidelné rozdělení napětí a přetvoření. V průměru však můžeme vytvořit rovinu přetvoření s parabolickým obdélníkovým průběhem, v němž lze zohlednit střední zakřivení.

Stávající stav napětí pro železobeton v ohybu

Pro model podle Quasta byly hodnoty výpočtu navrženy následovně

• pro pevnost v tahu f_ct,R

• pro přetvoření na trhliny ε_cr,R

Výpočtová hodnota pevnosti v tahu f_ct,R je tak menší, než stanoví Eurokód. Důvodem je popis vztahu napětí-přetvoření a stanovení redukčního parametru VMB, při kterém se předpokládané tahové napětí a výsledná tahová síla po překročení tahového přetvoření jen pomalu redukují. Při přetvoření 2 ⋅ ε_cr působí také napětí v tahu asi 0,95 ⋅ f_ct,R . V případě ohybu tak lze dobře předvídat redukci tuhosti. Pro čistý tah jsou výše uvedené hodnoty f_ct,R příliš malé. Podle Pfeiffera[2] by pro výpočet pevnosti v tahu měly být použity hodnoty z EC 2.
Hodnoty pro f_ct,R = 1/20 ⋅ f_cm, které doporučuje Quast [3], lze dosáhnout použitím 60 % pevností v tahu uvedených v EC 2. , lze při použití f_ct,R = 0.6 ⋅ fctm předpovědět vznik trhlin v průřezu příliš brzy. Na druhé straně se již zohledňuje snížení pevnosti v tahu při stálém zatížení (asi 70 %) nebo dočasně vyšší zatížení (např. krátkodobé použití kombinace vzácných účinků), které vede k poškozené tahové oblasti.
Jednotlivé výpočtové hodnoty pro tahovou oblast betonu lze popsat následovně:

Modifikovaný přístup podle Quast