Zurück zu Online-Handbüchern

268x

005724

11. Juli 2024

Handbuch wählen

Übersicht

Einführung

Theorie

Eingabedaten

Berechnung

Ergebnisse

Durchlässige Flächen

In RWIND 3 Pro ist es möglich, einer Oberfläche eine Permeabilität zuzuweisen. Eine kurze Theorie zur Permeabilität finden Sie in Kapitel Permeability. In RWIND 3 Pro wird die Permeabilität mithilfe einer Randbedingung modelliert, einem vorgeschriebenen Druckabfall auf definierten Oberflächen. Der Druckabfall (Druckgradient) wird durch die Gleichung angegeben:

@formula001242@

∆ p = - (D μ U + \frac{1}{2} I ρ {|\begin{matrix} U \end{matrix}|}^{2}) \cdot L

Δp[Pa]	Druckverlust
μ[Pa.s]	Dynamische Viskosität des Fluids
U[m/s]	Geschwindigkeit des Fluids
D[1/m²]	Darcy-Koeffizient
I[1/m]	Trägheitskoeffizient
ρ[kg/m³]	Dichte des Fluids
L[m]	Permeable media length in the flow direction

Druckverlust

wobei die Koeffizienten D und I definiert sind als:

@formula001244@

I = \frac{C_{F}}{\sqrt{α}}

C_F[-]	Forchheimer-Parameter
α[m²]	Durchlässigkeit

Trägheitskoeffizient

@formula001243@

D = \frac{1}{α}

α[m²]

Durchlässigkeit

Darcy-Koeffizient

In den in Kapitel Permeability besprochenen Modellen für durchlässige Medien wird auf der rechten Seite der N‑S-Gleichungen ein Quellterm im Schwerpunkt der Zellen hinzugefügt, in denen die Permeabilität gelöst werden soll. Da RWIND 3 Pro nur durchlässige Oberflächen löst (d.h. relativ dünne Elemente), wird die Permeabilität bisher mit einer zyklischen Randbedingung (porousBafflePressure) modelliert, indem der Druckgradient auf die ausgewählten Elemente (Patch) vorgeschrieben wird. Weitere Details finden Sie im OpenFOAM Guide. Dies ist ein rechnerisch einfaches Modell, und interessante Ergebnisse können in kurzer Rechenzeit erzielt werden. Es hat jedoch seine Einschränkungen, zum Beispiel kann die Verwendung des Modells für hohen Druckabfall nicht zu Konvergenz und Ergebnissen führen.

Weitere spezifische Informationen über das Permeabilitätsmodell (porousBafflePressure) finden Sie im OpenFOAM-4.1 Handbuch.

Permeabilität & Zonen

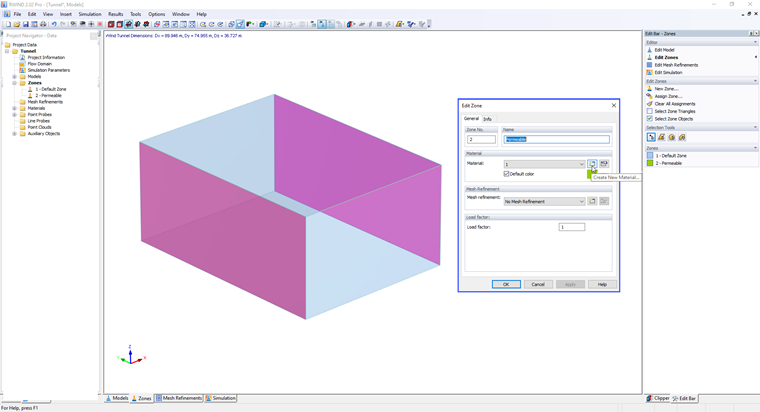
In RWIND 3 Pro wird die Permeabilität den ausgewählten Zonen als Materialeigenschaft zugewiesen, siehe das Bild unten.

@image035200@

Zonen und Durchlässigkeit

Im Dialogfeld "Zone bearbeiten", im Abschnitt "Material", klicken Sie auf "Neues Material erstellen..." oder "Material bearbeiten...". Es erscheint ein Dialogfeld mit Permeabilitätsparametern.

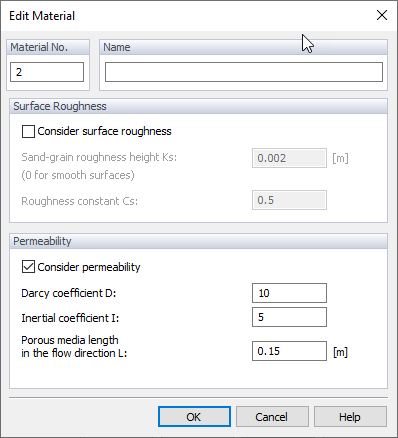
@image035201@

Bearbeiten von Material, Durchlässigkeit

Hier müssen die Permeabilitätskoeffizienten D und I sowie die Länge der durchlässigen Oberfläche (Dicke) L definiert werden. Eine Einführung, wie man diese Koeffizienten ableitet und erhält, wurde in Kapitel Permeability beschrieben. Weitere Ideen und Ansätze zur Ableitung der Koeffizienten finden Sie auch hier: Darcy-Forchheimer Calculator Eine Möglichkeit, den Koeffizienten zu erhalten und die Permeabilität zu modellieren, wird im Artikel der Wissensbasis auf der Dlubal-Website beschrieben.

KB | Verwendung der Funktion für durchlässige Flächen in RWIND Pro

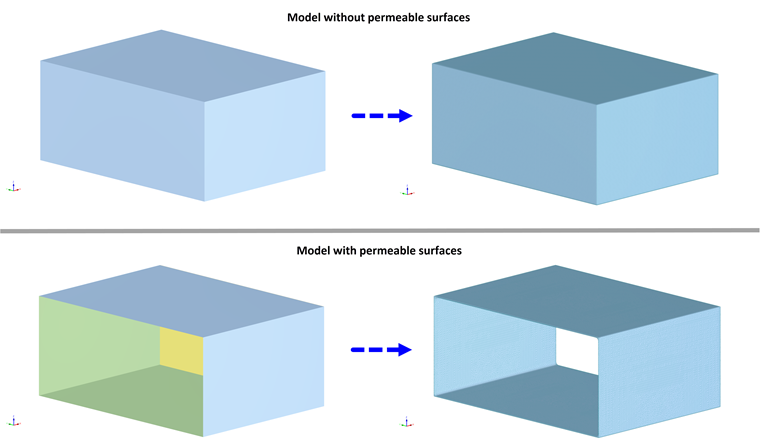
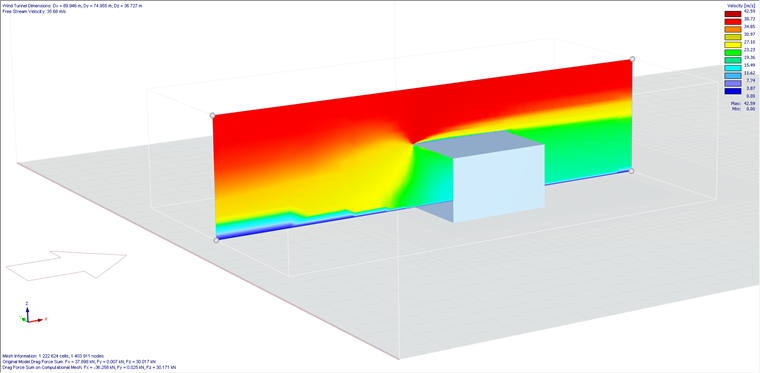
Nach der Einstellung aller Koeffizienten und der Zuordnung der Zonen zu den Oberflächen ist das Modell mit durchlässigen Oberflächen bereit für die Berechnung.

Tipp

Beim Festlegen der Koeffizienten D und I ist es wichtig, ihre physikalische Interpretation zu berücksichtigen. Der D-Koeffizient beeinflusst die Bedeutung der Reibungs-(viskosen) Kräfte, während der I-Koeffizient die Bedeutung der Trägheitskräfte der Geschwindigkeit beeinflusst, wenn der Fluss die durchlässige Oberfläche passiert.#

Wichtig

Die Berechnung mit der Oberflächenpermeabilität kann nur an vereinfachten Modellen durchgeführt werden. Das Shrink-Wrapping-Mesh stellt ein geometrisch korrektes Netz ohne offene Volumen sicher. Wenn die Modellvereinfachung deaktiviert ist, könnte das generierte Volumenmesh von geringer Qualität sein und die Ergebnisse könnten falsch sein. Hier ist es wichtig zu betonen, dass sich das vereinfachte Modell mit und ohne durchlässige Oberflächen erheblich unterscheidet; siehe das Bild „Modellnetz mit und ohne durchlässige Oberfläche“—das Modell mit durchlässigen Oberflächen bildet in diesem Fall ein offenes Volumenmodell, das dann zu einem größeren Volumenmesh führt, als dasselbe Modell ohne sie.

@image036323@

Vizualizace znázorňující dvě varianty sítě modelu, jednu s propustnou plochou a druhou bez ní.

Model sítě s propustnou plochou a bez propustné plochy

Wichtig

Das aktuelle Permeabilitätsmodell (OpenFOAM, porousBafflePressure) ist funktionsfähig für relativ einfache durchlässige Oberflächen (z. B. Drahtgeflechte, Lamellen, Barrieren usw.); d. h. einfache Formen, die durch eine Reihe von gleich orientierten Dreiecken definiert sind. Wenn wir also durchlässige Oberflächen für das gesamte Gebäude verwenden (zum Beispiel das "Eiffelturm"-Modell aus Project Manager), dann wird die Berechnung höchstwahrscheinlich instabil sein, die Ergebnisse werden falsch sein oder die Berechnung funktioniert überhaupt nicht.

@image035210@

Geschwindigkeitsfeld, durchlässige Flächen

Übergeordnetes Kapitel

Importierte Modelle