Shape Orthotropy

In the Shape Orthotropy tab, you can describe the orthotropic properties by means of geometric parameters. The program determines the stiffness matrix elements based on these specifications.

Dialog Box "New Thickness", Tab "Shape Orthotropy"

Orthotropy Type

Various types are available for selection in the list (see the image above). Define the geometric shape that corresponds to the orthotropic properties of the thickness.

The "Parameters" section is adapted to the orthotropy type so that you can describe the geometry appropriately. The individual types are described below in the Parameters description.

Orthotropy Direction

The orthotropic properties refer to the xy-axis system of the respective surfaces (see the graphics in the dialog box). If the stiffnesses do not correspond to the orientations of the surface axis system, you can adjust the direction in this section.

Adjusting Orthotropy Direction

A positive angle β rotates the orthotropic stiffnesses clockwise about the positive z-axis of the surface. The matrices are transformed accordingly and displayed in the Transformed Stiffness Matrix tab.

Consideration of Self-Weight

When using shape orthotropies, there are usually different thicknesses for both directions. Specify the thickness that the program should apply when determining the self-weight. The list provides the following "Self-weight definition" options:

• Determined from parameters: The notional thickness is determined from the parameters of the x- and y-directions.
• User-defined fictitious thickness: Define the thickness d_g manually.
• User-defined self-weight: Enter the self-weight w_g as mass per unit of area.

Parameters

In this section, define the geometric properties of the orthotropy type.

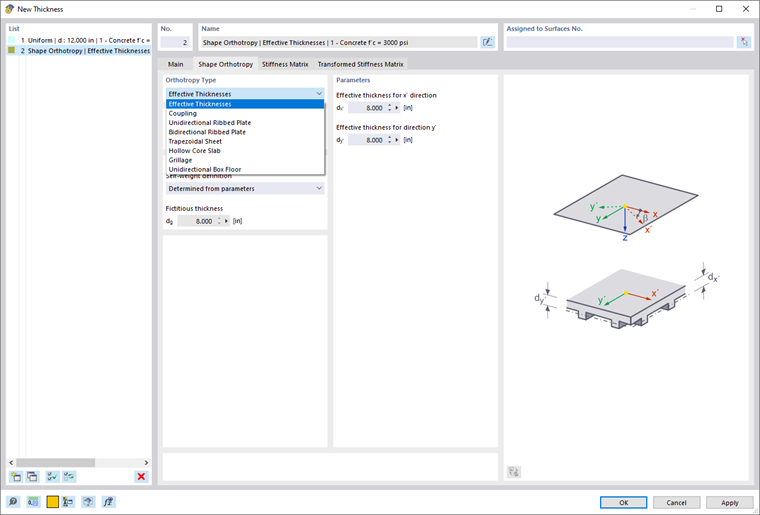
Effective Thicknesses

You can define different thicknesses in the orthotropy directions x and y to represent unequal stiffness ratios (see the image New Thickness).

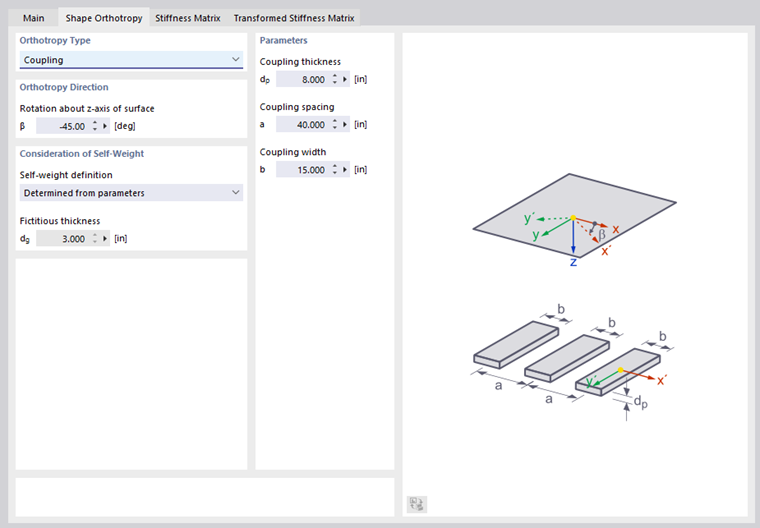
Coupling

With this orthotropy type, you can represent connections between surfaces or members that are available due to coupling elements.

Orthotropy Type "Coupling"

Enter the thickness of the coupling elements d_p, the center distance a, and the width of the coupling elements b according to the scheme. A realistic coupling model is given when the distance of the coupled elements is larger than their width.

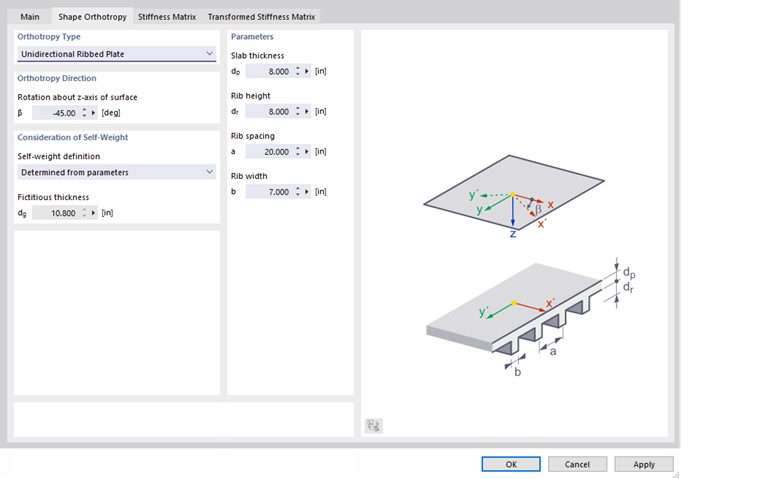
Unidirectional Ribbed Plate

The orthotropic properties of a ribbed floor are based on the principle of a uniaxially stressed T-beam slab.

Orthotropy Type "Unidirectional Ribbed Plate"

Enter the slab thickness d_p, the rib height d_r, the rib spacing a, and the rib width b according to the scheme. Based on these parameters, RFEM determines the stiffnesses for each direction.

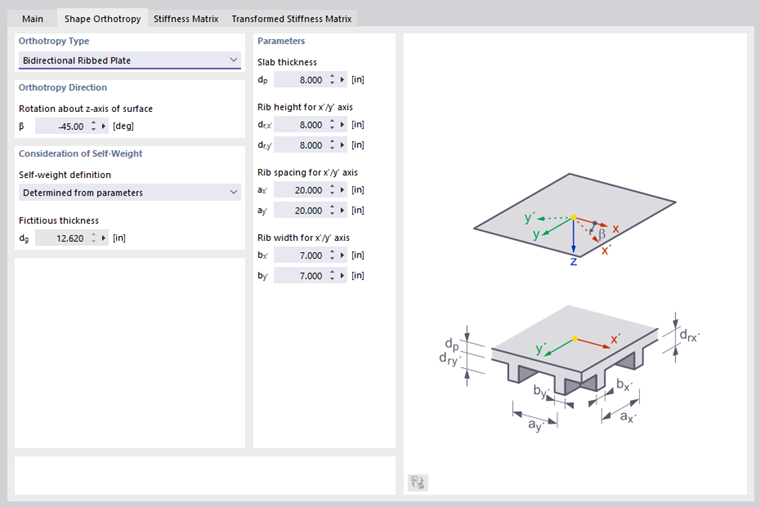
Bidirectional Ribbed Plate

This type of ceiling is characterized by webs that cross each other orthogonally in a uniform grid, thus dividing the floor into coffers.

Orthotropy Type "Bidirectional Ribbed Plate"

Enter the slab thickness d_p and the rib height d_r as well as the rib spacing a, and the rib width b according to the scheme.

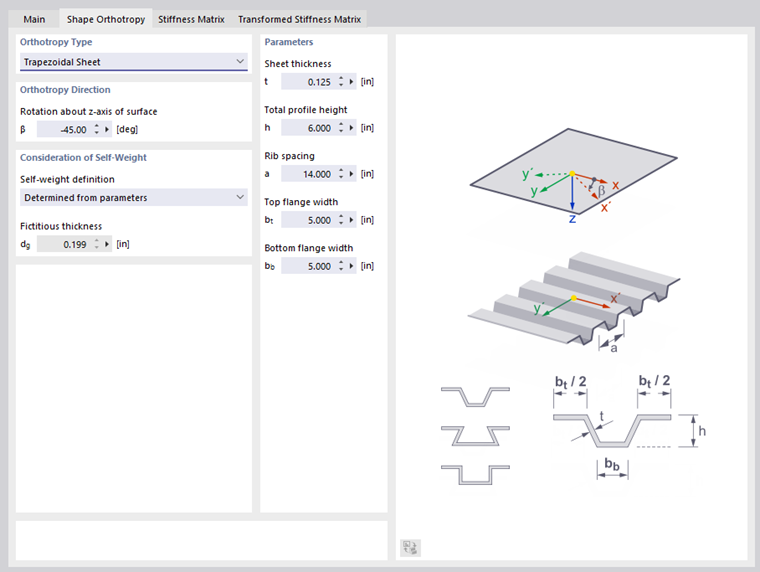
Trapezoidal Sheet

You can display a trapezoidal sheet not only as a member, but as a surface with orthotropic properties.

Orthotropy Type "Trapezoidal Sheet"

Enter the sheet thickness t, the total profile height h, and the center distance of the ribs a, as well as the top flange width b_t and the bottom flange width b_b according to the scheme.

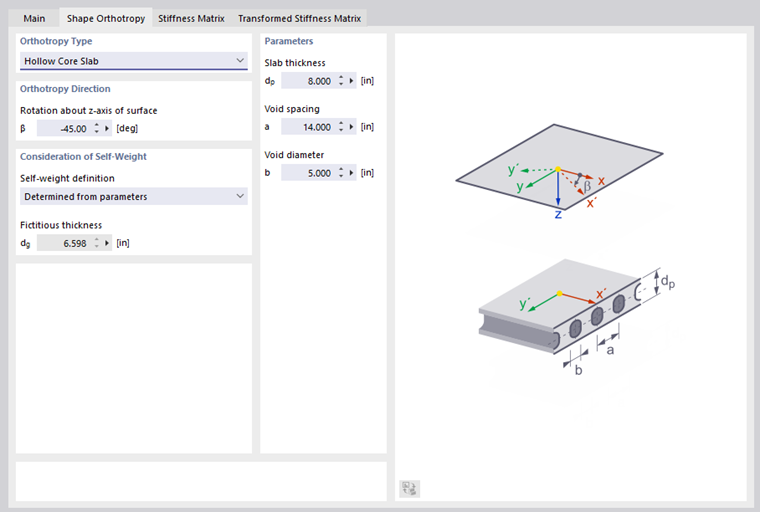
Hollow Core Slab

Hollow units built in a ceiling reduce the self-weight, but produce orthotropic structural behavior.

Orthotropy Type "Hollow Core Slab"

Enter the slab thickness d_p, the void spacing a, and the void diameter b according to the scheme.

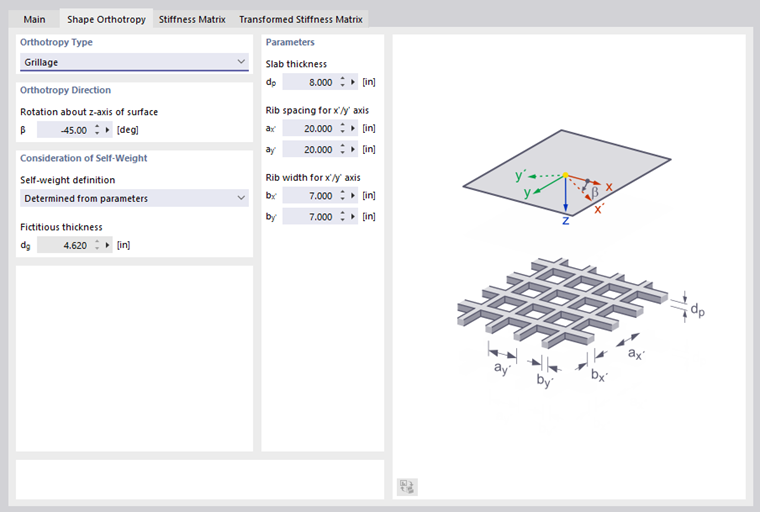
Grillage

You can display a grillage not only as a member model, but as a surface with orthotropic properties.

Orthotropy Type "Grillage"

Enter the slab thickness d_p, the center distances of the ribs a, and the rib widths b for both axes according to the scheme.

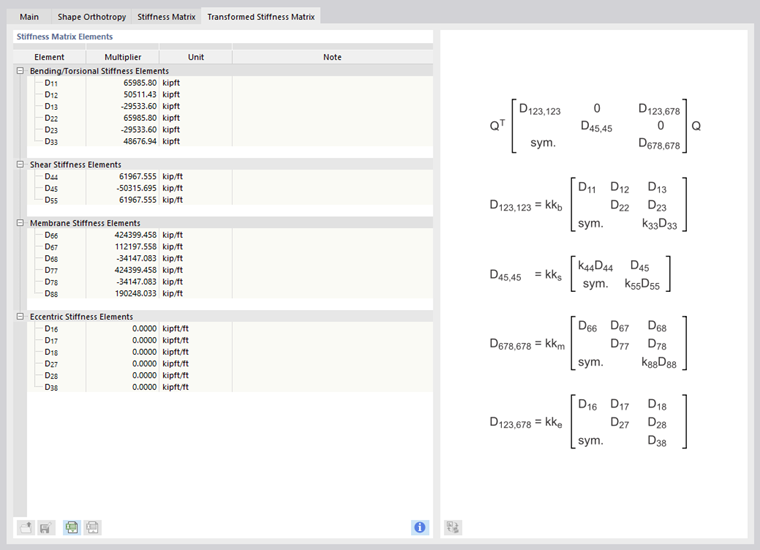
Stiffness Matrix

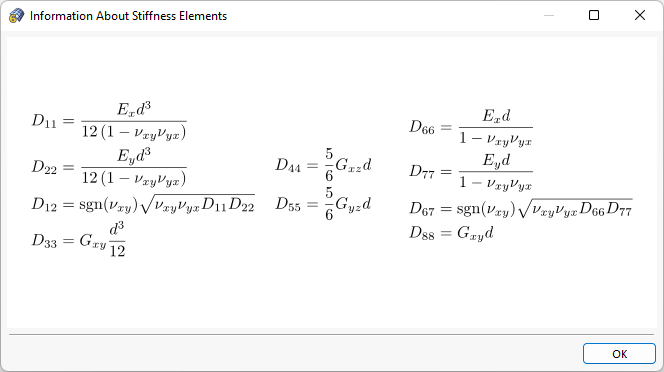
The Stiffness Matrix tab of the "New Thickness" dialog box shows the stiffness matrix elements (see the image Defining Stiffness Matrix ). The entries cannot be changed.

Transformed Stiffness Matrix

If the axes of the orthotropy are not consistent with the axes of the coordinate system of elements, you have to transform the matrices. The corresponding values are displayed in the Transformed Stiffness Matrix tab.

Transformed Stiffness Matrix Elements

Use the button to open a dialog box with information for determining the matrix elements.

Information About Stiffness Elements