Rejestr Podstawowe zarządza podstawowymi parametrami pręta. Jeśli zaznaczysz pole wyboru w sekcji 'Opcje', zazwyczaj do dialogu dodawana jest dodatkowa zakładka. Tam można określić szczegóły.
Typ pręta
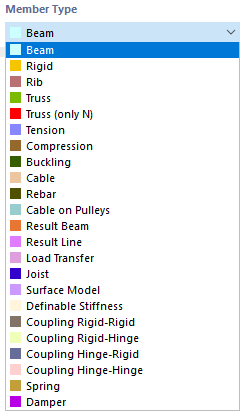
Typ pręta określa, w jaki sposób można przeprowadzać analizy sił wewnętrznych lub jakie właściwości są zakładane dla pręta. W menu wyboru dostępne są różne typy prętów.
Belka
Belka to pręt odporny na zginanie, który może przenosić wszystkie rodzaje sił wewnętrznych. Pręt belkowy nie ma przegubów na końcach. Ten typ pręta może być obciążony wszystkimi rodzajami obciążeń.
Pręt sztywny
Pręt sztywny łączy przemieszczenia dwóch węzłów za pomocą sztywnego połączenia. Dlatego odpowiada zasadniczo sprężynie. Umożliwia to zdefiniowanie prętów o bardzo wysokiej sztywności z uwzględnieniem przegubów, które mogą posiadać również stałe sprężyny i nieliniowości. Prymatycznie nie występują problemy numeryczne, ponieważ sztywność jest dopasowana do systemu.
Dla prętów sztywnych można uzyskać siły wewnętrzne, jeśli w Nawigatorze - Wyniki, w kategorii 'Pręty' aktywujesz opcję Wyniki dla połączeń.
Dla prętów sztywnych przyjmuje się następujące sztywności:
| Sztywność na ściskanie E · A | 1013 · ℓ [jednostki SI] z ℓ = długość pręta |
| Sztywność na skręcanie G · IT | 1013 · ℓ [jednostki SI] |
| Sztywność na zginanie E · I | 1013 · ℓ3 [jednostki SI] |
| Sztywność na ścinanie GAy / GAz (jeśli włączono) | 1016 · ℓ3 [jednostki SI] |
Pręt żeberkowy
Dzięki żebrom można modelować belki płytowe (podciągi). W tym typie pręta uwzględniane są w modelu MES ekscentryczności i współpracujące szerokości płyt.
Żebra najlepiej nadają się do prętów żelbetowych, ponieważ siły wewnętrzne i przekroje żeber wpływają na obliczenia żelbetowe. Blacha stalowa z przyspawanym „żebrem” powinna być modelowana jako powierzchnia z ekscentrycznie podłączonym prętem.
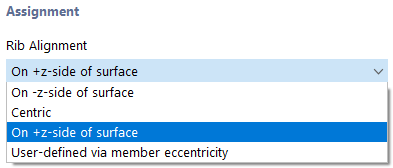
Lista 'Układ żeber' oferuje kilka opcji wyboru.
Żebro jest zwykle prętem umieszczonym ekscentrycznie. Ekscentryczność obliczana jest automatycznie jako połowa grubości powierzchni i połowa wysokości pręta. Można ją jednak również zdefiniować ręcznie. Przez ekscentryczność żebra zwiększa się sztywność modelu. Przy ustawieniu środkowym oś główna żebra leży w środku powierzchni.
Współpracujące szerokości żebra należy zdefiniować w sekcji 'Wymiary kołnierzy' dla strony lewej i prawej. Zazwyczaj można zachować opcję 'Znajdź automatycznie', dzięki której program określa obie powierzchnie. Jeśli na linii pręta żeberkowego spotyka się więcej niż dwie powierzchnie, należy ręcznie ustawić decydujące powierzchnie.
Istnieją różne możliwości wprowadzenia szerokości integracyjnych b-y,int i b+y,int (patrz obrazek Nowe żebro): szerokości można wprowadzić bezpośrednio lub automatycznie określić z długości pręta, korzystając z opcji Lref / 6 i Lref / 8. Można je również określić zgodnie z wytycznymi określonej normy, na przykład według 'EC2', sekcji 5.3.2.1.
Wartości by,int określają szerokość obszaru powierzchniowego lub obszaru wpływu, z którego należy zintegrować siły wewnętrzne. Wartości by,eff reprezentują szerokość przekroju kołnierza żebra od środka środka do krawędzi. Domyślnie wartości by,int i by,eff są równe. Można je jednak zdefiniować osobno po kliknięciu przycisku
![]() .
.
Jeśli zdefiniowano węzły typu 'Węzły na pręcie', żebro może być zdefiniowane sekcyjnie dla poszczególnych segmentów. Jeśli zdefiniowano wiele segmentów, kaskadowe szerokości wpływu mogą być liniowo połączone poprzez kolumnę tabeli 'Liniowe rozłożenie', aby uniknąć dużych skoków sztywności w pręcie żeberkowym.
W modelach 3D współpracujące szerokości nie wpływają na sztywność, ponieważ zwiększona sztywność jest uwzględniana przez ekscentryczny pręt. Jednakże współpracujące szerokości wpływają na rozkład sił wewnętrznych w pręcie i na powierzchni.
Kratownicowy
Pręt kratownicowy odpowiada prętowi belkowemu z przegubami momentowymi na obu końcach. Dodatkowo skręt wokół osi podłużnej na początku pręta jest zwolniony przez przegub φx. W przypadku tego typu pręta siły zginające i skręcające wynikające z obciążeń pręta są wyprowadzane.
Kratownicowy (tylko N)
Ten rodzaj pręta kratownicowego o sztywności E ⋅ A jest w stanie przenosić siły osiowe w postaci ściskania i rozciągania. Wprowadzane są jedynie siły wewnętrzne na końcowych węzłach. Pręt wykazuje liniowy przebieg sił wewnętrznych, o ile na pręcie nie działa obciążenie punktowe. Nie jest generowany przebieg momentu, który mógłby powstać wskutek ciężaru własnego lub obciążenia liniowego. Jednakże siły węzłowe są obliczane z obciążeń prętowych, co zapewnia prawidłowe przekazywanie obciążeń.
Pręt rozciągający
Pręt rozciągający może przenosić jedynie siły rozciągające. Typ pręta odpowiada 'Kratownicy (tylko N)', która ulega awarii przy obciążeniu ściskającym.
Obliczenia modelu prętowego z prętami rozciągającymi są przeprowadzane iteracyjnie: W pierwszym kroku określa się siły wewnętrzne wszystkich prętów. Jeśli pręty rozciągające otrzymują negatywne siły osiowe (ściskanie), rozpoczynany jest kolejny krok iteracyjny. Udział sztywności tych prętów nie jest już uwzględniany – są one uznane za wyczerpane. Proces ten jest kontynuowany aż do momentu, gdy żaden pręt rozciągający nie ulegnie awarii. System może stać się niestabilny w wyniku awarii prętów rozciągających.
Pręt ściskający
Pręt ściskający może przenosić jedynie siły ściskające. Typ pręta odpowiada 'Kratownicy (tylko N)', która ulega awarii przy obciążeniu rozciągającym. Pręty ściskające, które ulegają awarii, mogą prowadzić do niestabilności systemu.
Pręt wyboczeniowy
Pręt wyboczeniowy odpowiada 'Kratownicy (tylko N)', która nieograniczenie przenosi siły rozciągające, ale siły ściskające tylko do osiągnięcia krytycznej siły. Dla przypadku Eulera 2 krytyczna siła jest określana w następujący sposób:
Tym typem pręta można często unikać niestabilności, które powstają podczas nieliniowych obliczeń według drugiej lub trzeciej teorii porządku wskutek wyboczenia prętów kratownicowych. Zastępując je (realistycznie) prętami wyboczeniowymi, w wielu przypadkach zwiększa się krytyczne obciążenie.
Lina
Lina może przenosić jedynie siły rozciągające. Pozwala to na modelowanie łańcuchów linowych za pomocą obliczeń iteracyjnych według trzeciej teorii porządku z uwzględnieniem sił podłużnych i poprzecznych.
Liny są odpowiednie dla modeli, w których mogą występować duże odkształcenia wraz z odpowiednimi zmianami sił wewnętrznych. Dla prostych naprężeń, takich jak w przypadku zadaszenia, pręty rozciągające są w pełni wystarczające.
Pręt zbrojeniowy
Ten typ pręta pozwala na modelowanie bezprzeponowych stalowych wzmocnień w modelu MES elementu żelbetowego. Można badać na przykład obszary nieciągłości, oparte na analogii kratowej (cięcie i odchylenie przy konsolach, belki z otworami).
Pręt zbrojeniowy ma automatyczną funkcję połączenia z innymi elementami, takimi jak pręty lub powierzchnie, gdy znajduje się fizycznie w elemencie. Podobnie jak kratownica (tylko N), pręt zbrojeniowy ma jedynie sztywność styczną. Obecnie nieliniowe zachowanie materiału nie jest jeszcze możliwe.
W sekcji 'Ustawienia' ustawiony jest jako typ pręta słabe zbrojenie. Inne typy prętów zbrojeniowych są dostępne, gdy aktywowane jest rozszerzenie Spannglieder.
Przypisz pręty lub powierzchnie, w których znajduje się pręt zbrojeniowy, w sekcji 'Obiekty główne'. Użyj do tego przycisku
![]() . Następnie możesz automatycznie połączyć pręt zbrojeniowy z obiektem głównym za pomocą przycisku
. Następnie możesz automatycznie połączyć pręt zbrojeniowy z obiektem głównym za pomocą przycisku
![]() .
.
Lina na rolkach
Ten typ pręta linowego również przenosi tylko siły rozciągające i jest obliczany na podstawie teorii lin (trzecia teoria porządku). Pręt linowy na rolkach można jednak zdefiniować jedynie na polilinii o minimalnie trzech węzłach. Ten typ pręta jest odpowiedni dla elementów napiętych na zginanie, których siły podłużne są przekazywane przez punkty odchylenia w modelu. Przykładem zastosowania może być wielokrążek.
W przeciwieństwie do zwykłego liny, w wewnętrznych węzłach możliwe jest tylko przesunięcie w kierunku podłużnym (ux). Dlatego pręt nie może być obciążany siłami działającymi w lokalnym kierunku y lub z. Uwzględniane są jedynie przemieszczenia ux i siły osiowe N.
W wewnętrznych węzłach polilinii nie ma znaczenia, czy występuje złoże węzłowe, czy pręt jest połączony z inną konstrukcją: system całkowity pręta linowego jest analizowany na całej długości polilinii.
Pręt wynikowy
Pręt wynikowy nadaje się do integrowania wyników powierzchniowych, objętościowych lub prętowych w pręcie fikcyjnym. Umożliwia to na przykład odczytywanie wynikających sił poprzecznych powierzchni w celu sprawdzenia muru.
Linia pręta wynikowego może być dowolnie umieszczona w modelu. Pręt wynikowy nie wymaga ani podparcia, ani połączenia z modelem. Trzeba mu jednak przypisać przekrój, aby umożliwić obliczenia. Na pręcie wynikowym nie można umieszczać obciążeń.
Wybierz w sekcji 'Integruj napięcia i siły' typ pręta wynikowego, aby określić geometryczny kształt obszaru integracji. W sekcji 'Parametry' można następnie zdefiniować wymiary. Odnoszą się one do linii pręta w jego środku ciężkości.
W sekcji 'Uwzględnij obiekty' określ powierzchnie, komórki powierzchniowe, ciała objętościowe i pręty, których wyniki będą brane pod uwagę przy integracji. Alternatywnie wybierasz 'Wszystkie' obiekty i wyłączasz konkretne elementy w sekcji 'Wyłączone z uwzględnianych obiektów'.
Linia wynikowa
Linia wynikowa nadaje się do integrowania wyników powierzchni, objętości lub prętów w linii. Ta linia może być dowolnie umieszczona w modelu.
Zasada odpowiada Prętowi wynikowemu. Nie trzeba jednak przypisywać żadnego przekroju. W zakładce 'Przekrój' można odczytać długość linii i ewentualnie obrócić linię wynikową dla wyświetlania wyników; nie ma to żadnych innych funkcji.
Przeniesienie ładunku
Ten typ pręta pozwala na przenoszenie obciążeń na obiekty, które są połączone z prętem na jego końcach lub w węzłach pośrednich. Sam pręt nie ma sztywności. Kryteria przeniesienia ładunku można określić na nowej zakładce.
Przeniesienie ładunku odbywa się obecnie metodą pasków. Obciążenie pręta przenoszącego ładunek – obciążenie prętowe lub obciążenie węzłowe typu siła, moment lub masa – jest proporcjonalnie rozkładane na najbliższe wspólne obiekty strukturalne. Mogą to być na przykład podpory węzłowe, pręty, węzły powierzchniowe lub obiektu podparte linie.
Jeśli należy uwzględnić ciężar własny pręta, można w sekcji 'Parametry' wprowadzić wagę pręta.
W sekcji 'Obiekty obciążane' są podawane numery węzłów, w których obciążenie prętowe jest przenoszone na sąsiednie obiekty. Jeśli nie wszystkie te węzły są istotne, można wykluczyć określone węzły w sekcji 'Bez wpływu na'.
Wirtualny nośnik
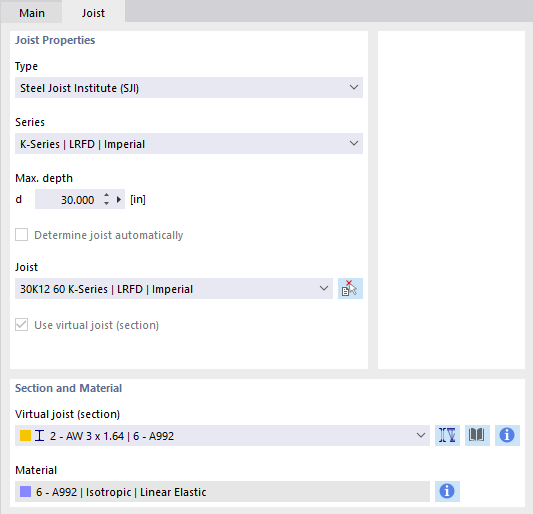
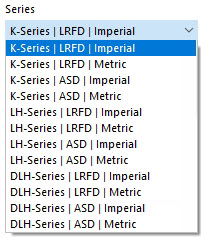
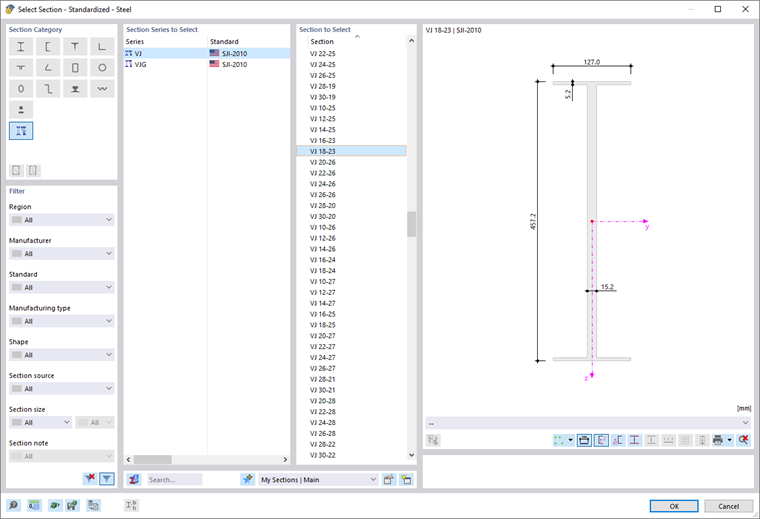
Ten typ pręta umożliwia przyjęcie właściwości przekroju dla Open Web Steel Joists, które są zamieszczone przez Steel Joist Institute w tak zwanych "Virtual Joist" tabelaach. Te profile Virtual Joist reprezentują równoważne belki z szerokim pasem, które bardzo dobrze odwzorowują powierzchnię pasów, efektywne momenty bezwładności i wagę nośnika. Belka jest zatem zastępowana przez pręt z wirtualnym przekrojem. Pozwala to na modelowanie w całym systemie złożonych jednostek nośnych, takich jak kratownice.
Wybierz w menu opcję 'Seria wirtualna'.
W menu 'Wirtualna belka' możesz określić dokładny typ.
Przycisk
![]() w sekcji 'Przekrój i materiał' umożliwia import wirtualnej belki z biblioteki przekrojów.
w sekcji 'Przekrój i materiał' umożliwia import wirtualnej belki z biblioteki przekrojów.
Model powierzchniowy
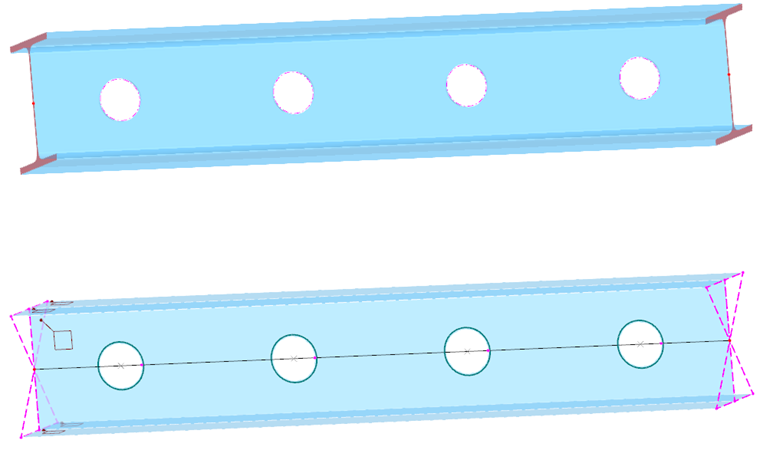
Ten typ pręta jest odpowiedni przede wszystkim do modelowania perforowanych i komórkowych nośników lub osłabień przekroju, takich jak otwory dla przewodów instalacyjnych w modelu prętowym. Pręt jest konwertowany na model powierzchniowy, w którym otwory prętowe są umieszczane zgodnie z danymi użytkownika. Pręt nadal istnieje. Muszą być spełnione następujące warunki:
- Przekrój to udokumentowany lub parametrystyczny profil cienkościenny z jednym środnikiem.
- Materiał przekroju oparty jest na izotropowym modelu materiału liniowo-sprężystym.
W przypadku typu pręta 'Model powierzchniowy' pręt występuje zarówno jako pręt, jak i obiekt powierzchniowy. Właściwości geometryczne są identyczne; oba modela mają wspólny środek ciężkości. Wyświetlanie jest kontrolowane w Nawigatorze - Wyświetlanie za pomocą wpisu Model → Obiekty podstawowe → Pręty → Model powierzchniowy lub za pomocą przycisku
![]() na pasku narzędzi.
na pasku narzędzi.
Siatka MES modelu powierzchniowego jest tworzona automatycznie, obecnie nie można jej zmienić. Do obliczeń statycznych stosowany jest model powierzchniowy. Następnie dostępne są zarówno wyniki prętów (jak w pręcie wynikowym, w którym napięcia części przekrojów prętów są integrowane w siły w pręcie), jak i wyniki powierzchniowe. Kontrolę można również wykonać poprzez Nawigator - Wyświetlanie lub przycisk
![]() .
.
Obliczenia prętów modelu powierzchniowego w rozszerzeniach są przeprowadzane z siłami w prętach i przekroju pręta.
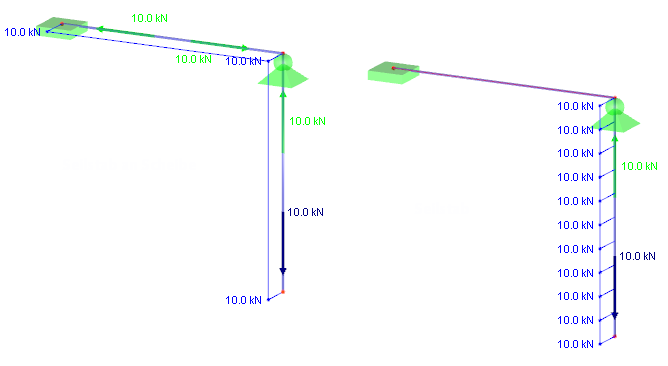
Jak widać na powyższym obrazku, na końcach pręta modelu powierzchniowego powstaje kilka sztywnych prętów. Łączą model powierzchniowy z węzłami końcowymi sąsiednich prętów. Umożliwia to prawidłowe przekazywanie sił wewnętrznych do obiektów 1D. Jeśli kilka prętów modelu powierzchniowego łączy się ze sobą, te pręty połączeniowe są generowane dla każdego pręta.
Zdefiniuj w tym przypadku dla obciążenia prętowego ekscentryczność siły na przekroju. Obciążenie będzie wtedy realistycznie przyłożone do krawędzi przekroju i pozostanie również w modelu powierzchniowym.
Sztywność
Ten typ pręta pozwala na użycie pręta o niestandardowych sztywnościach. Wartości sztywności są zdefiniowane w dialogu 'Nowa sztywność pręta' (patrz rozdział Sztywności prętów).
Sprzężenie
Pręt sprzęgający to wirtualny, bardzo sztywny pręt z końcówkami sztywnymi lub przegubowymi. Dostępne są cztery możliwości wyboru, aby połączyć stopnie swobody węzłów początkowych i końcowych 'Sztywne' lub przez 'Przegub'. Umożliwia to modelowanie specjalnych sytuacji dotyczących przekazywania sił i momentów. Siły podłużne i poprzeczne, a także momenty skręcające i zginające są bezpośrednio przenoszone z węzła do węzła.
Sprężyna
Pręt sprężynowy umożliwia modelowanie właściwości sprężystych, zarówno liniowych, jak i nieliniowych, z możliwością definiowania obszarów działania. Dla pręta sprężynowego ustawisz w sekcji 'Przekrój' tylko długość pręta Lz, brak przekroju: Sztywność pręta wynika z parametrów sprężyny, które zdefiniujesz w dialogu 'Nowa sprężyna prętowa' (patrz rozdział Sprężyny prętowe).
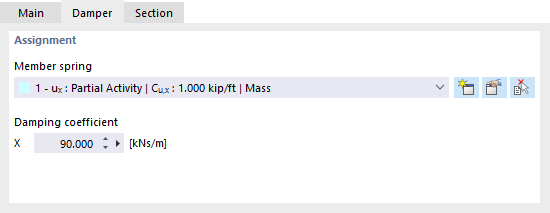
Tłumik
Tłumik zasadniczo odpowiada sprężynie prętowej z dodatkowymi właściwościami 'Współczynnik tłumienia'. Ten typ pręta rozszerza możliwości analizy dynamicznej według procedury czasowozmienna.
Jak w przypadku sprężyny prętowej, ustawisz w sekcji 'Przekrój' tylko długość pręta Lz, brak przekroju. Sztywność pręta wynika z parametrów sprężyny, które zdefiniujesz w dialogu 'Nowa sprężyna prętowa' (patrz rozdział Sprężyny prętowe). Możesz kontrolować właściwości tłumienia za pomocą współczynnika tłumienia X.
Opcje
W tej sekcji możesz określić dodatkowe właściwości prętów za pomocą pól wyboru.
Węzły na pręcie
Za pomocą jednego lub kilku węzłów na pręcie można podzielić pręt na segmenty, nie dzieląc go (patrz rozdział Węzły ).
Przeguby
Możesz dodać przeguby do pręta, aby sterować przekazywaniem sił wewnętrznych do węzłów końcowych (patrz rozdział Przeguby końców prętów). Dla niektórych typów prętów wprowadzanie przegubów jest zablokowane, ponieważ są już w istniejące przeguby wewnętrzne. Możesz przypisać przeguby oddzielnie dla 'Początku pręta i' i 'Końca pręta j'.
Ekscentryczności
Ekscentryczności oferują możliwość podłączenia pręta do węzłów końcowych w sposób ekscentryczny (patrz rozdział Ekscentryczności prętów). Możesz przypisać oddzielnie ekscentryczności do 'Początku pręta i' i 'Końca pręta j'.
Podparcia
Możesz przypisać podparcie do pręta, które działa na całej jego długości. Stopnie swobody i sztywności sprężyn są zdefiniowane w warunkach podparcia (patrz rozdział Podparcia prętowe).
Przewiązki
Przewiązki na pręcie wpływają na sztywność skrętną pręta. Mają one wpływ na obliczenia z użyciem skręcenia ze sztywnością krzyżową z uwzględnieniem siedmiu stopni swobody (patrz rozdział Przewiązki prętowe).
Otwory w prętach
Otwory w prętach wpływają na wartości przekroju i przebieg sił wewnętrznych. Są one istotne w przypadku typu pręta 'Model powierzchniowy'. W rozdziale Otwory prętowe opisano, jak zdefiniować typ i lokalizację otworów.
Nieliniowość
Możesz przypisać nieliniowość do pręta. Nieliniowe właściwości są definiowane jako nieliniowości prętowe (patrz rozdział Nieliniowości prętowe).
Punkty pośrednie
Punkty pośrednie umożliwiają kontrolowanie wyjścia wyników w tabeli wzdłuż pręta. Punkty podziału są zdefiniowane w dialogu 'Nowy punkt pośredni wyniku pręta' (patrz rozdział Punkty pośrednie wyniku pręta).
Modyfikacje końców
Modyfikacje końców pozwalają na graficzne dostosowanie geometrii pręta na jego końcach. Można przygotować przedłużenia, skrócenia lub ścięcia dla wizualizacji renderowanej.
'Przedłużenie': Można zdefiniować 'Przedłużenie' dla początku pręta i końca pręta. Negatywna wartość Δ będzie działała jako skrócenie.
'Nachylenie': Możesz ściąć każde zakończenie pręta z nachyleniem. Możliwe są kąty nachylenia wokół obu osi pręta y i z. Dodatni kąt powoduje obrót zgodnie z ruchem wskazówek zegara wokół odpowiedniej osi dodatniej.
Włącz transmisję obciążenia
Pole wyboru umożliwia podzielenie obciążenia pręta bez względu na jego sztywność po podziale obciążenia. W ten sposób pręt działa jako sztywność w modelu. Dystrybucja obciążenia na sąsiadujące obiekty jest kontrolowana przez parametry ustawione w zakładce Przeniesienie ładunku.
Dezaktywacja dla obliczeń
Gdy zaznaczysz to pole wyboru, pręt wraz z obciążeniem nie będzie uwzględniany w obliczeniach. Dzięki temu możesz badać, jak zachowanie konstrukcji zmienia się, gdy określone pręty nie działają. Pręty nie muszą być usuwane; obciążenia również pozostają bez zmian.