Powrót do Instrukcji online

12939x

002715

Dipl.-Ing. (FH) Robert Vogl

2023-12-15

Wybór ręczny

Przegląd

Graficzny interfejs użytkownika i jego ustawienia

Dlubal Center

Dane podstawowe modelu

Konstrukcja

Imperfekcje

Przypadki obciążeń i kombinacje

Asystenci obciążeń

Obciążenia

Obiekty wynikowe

Obliczenia

Wyniki

Obiekty pomocnicze

Funkcje programu

Wizualizacja wyników

Raport

Naprężenia

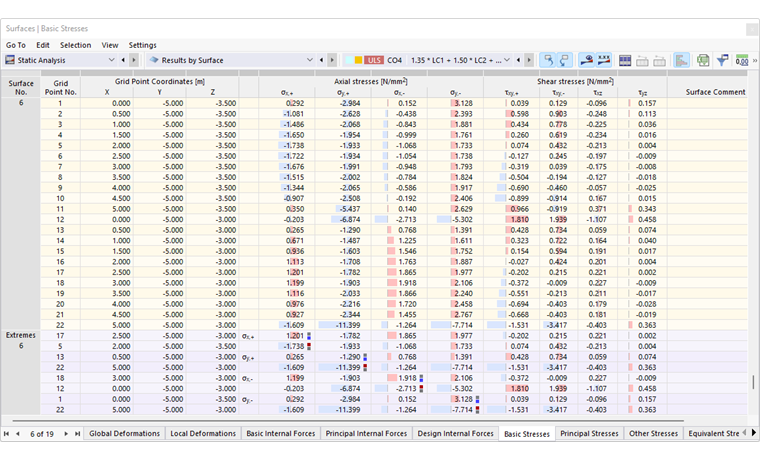
Określ w nawigatorze, które naprężenia mają być wyświetlane na powierzchniach. Tabela wymienia naprężenia każdej powierzchni według ustalonych w Menedżerze tabel wyników kryteriów.

Wybór naprężeń powierzchniowych w Nawigatorze

Naprężenia powierzchniowe w tabeli

Naprężenia powierzchniowe podzielone są na następujące kategorie:

Naprężenia podstawowe: naprężenia w kierunku osi powierzchni
Naprężenia główne: naprężenia w kierunku osi głównych
Składowe naprężeń sprężystych: naprężenia z momentów oraz z sił normalnych
Naprężenia równoważne: naprężenia według różnych hipotez naprężeń równoważnych

Naprężenia podstawowe

Naprężenia podstawowe odnoszą się do kierunków lokalnych osi powierzchni. W przypadku powierzchni zakrzywionych odnoszą się do lokalnych osi poszczególnych elementów skończonych (zobacz rysunek Wyświetlenie systemu osi FE ).

Naprężenia podstawowe są przedstawione na rysunku Siły wyboczeniowe i naprężenia powierzchniowe . Oznaczają one szczegółowo:

σ_{x, +} = \frac{n_{x}}{d} + \frac{6 m_{x}}{d^{2}}

d	Grubość powierzchni

Naprężenie σ_x,+ (w kierunku lokalnej osi x po dodatniej stronie powierzchni)

σ_{y, +} = \frac{n_{y}}{d} + \frac{6 m_{y}}{d^{2}}

Naprężenie σ_y,+ (w kierunku lokalnej osi y po stronie powierzchni dodatniej)

σ_{x, -} = \frac{n_{x}}{d} - \frac{6 m_{x}}{d^{2}}

Naprężenie σ_x,- (w kierunku osi x po stronie powierzchni ujemnej)

σ_{y, -} = \frac{n_{y}}{d} - \frac{6 m_{y}}{d^{2}}

Naprężenie σ_y,- (w kierunku osi y po stronie powierzchni ujemnej)

τ_{x y, +} = \frac{n_{x y}}{d} + \frac{6 m_{x y}}{d^{2}}

Naprężenie skręcające τ_xy,+ po stronie powierzchni dodatniej

τ_{x y, -} = \frac{n_{x y}}{d} - \frac{6 m_{x y}}{d^{2}}

Naprężenie skręcające τ_xy,- na powierzchni ujemnej

τ_{x z} = \frac{3 v_{x}}{2 d}

Naprężenie ścinające τ_xz prostopadłe do powierzchni w kierunku osi x

τ_{y z} = \frac{3 v_{y}}{2 d}

Naprężenie ścinające τ_yz prostopadłe do powierzchni roboczej w kierunku osi y

Naprężenia główne

Podczas gdy naprężenia podstawowe odnoszą się do układu współrzędnych xyz powierzchni, naprężenia główne stanowią wartości ekstremalne naprężeń w elemencie powierzchniowym. Osie główne 1 (maksymalna wartość) i 2 (minimalna wartość) są rozłożone ortogonalnie. Można wyświetlić kierunki osi głównych α graficznie jako trajektorie (porównaj rysunek Wyświetlenie trajektorii osi głównych ).

Naprężenia główne są określane z naprężeń podstawowych w następujący sposób:

σ_{1, +} = \frac{1}{2} [σ_{x, +} + σ_{y, +} + \sqrt{{(σ_{x, +} - σ_{y, +})}^{2} + 4 {τ_{x y, +}}^{2}}]

Naprężenie σ_1,+ w kierunku osi głównej 1 po stronie powierzchni dodatniej

σ_{2, +} = \frac{1}{2} [σ_{x, +} + σ_{y, +} - \sqrt{{(σ_{x, +} - σ_{y, +})}^{2} + 4 {τ_{x y, +}}^{2}}]

Naprężenie σ_2,+ w kierunku osi głównej 2 po stronie powierzchni dodatniej

α_{+} = \frac{1}{2} \arctan 2 (\frac{2 τ_{x y, +}}{σ_{x, +} - σ_{y, +}}) \in (- 90 °, 90 °]

Kąt α₊ pomiędzy lokalną osią x (lub y) a osią główną 1 (lub 2) dla naprężeń po stronie powierzchni dodatniej

σ_{1, -} = \frac{1}{2} [σ_{x, -} + σ_{y, -} + \sqrt{{(σ_{x, -} - σ_{y, -})}^{2} + 4 {τ_{x y, -}}^{2}}]

Naprężenie σ_1,- w kierunku osi głównej 1 na stronie powierzchni ujemnej

σ_{2, -} = \frac{1}{2} [σ_{x, -} + σ_{y, -} - \sqrt{{(σ_{x, -} - σ_{y, -})}^{2} + 4 {τ_{x y, -}}^{2}}]

Naprężenie σ_2,- w kierunku osi głównej 2 na powierzchni ujemnej

α_{-} = \frac{1}{2} \arctan 2 (\frac{2 τ_{x y, -}}{σ_{x, -} - σ_{y, -}}) \in (- 90 °, 90 °]

Kąt α_- pomiędzy lokalną osią x (lub y) a osią główną 1 (lub 2) dla naprężeń po stronie powierzchni ujemnej

σ_{1, m} = \frac{1}{2} [σ_{x, m} + σ_{y, m} + \sqrt{{(σ_{x, m} - σ_{y, m})}^{2} + 4 {τ_{x y, m}}^{2}}]

Naprężenie membranowe σ_1,m w kierunku osi głównej 1

σ_{2, m} = \frac{1}{2} [σ_{x, m} + σ_{y, m} - \sqrt{{(σ_{x, m} - σ_{y, m})}^{2} + 4 {τ_{x y, m}}^{2}}]

Naprężenie membranowe σ_2,m w kierunku osi głównej 2

α_{m} = \frac{1}{2} \arctan 2 (\frac{2 τ_{x y, m}}{σ_{x, m} - σ_{y, m}}) \in (- 90 °, 90 °]

Kąt α_m pomiędzy lokalną osią x a osią główną 1 dla naprężeń membranowych

τ_{\max} = \sqrt{{τ_{x z}}^{2} + {τ_{y z}}^{2}}

Maksymalne naprężenie ścinające τ_max prostopadle do powierzchni

Inne naprężenia / Składowe naprężeń sprężystych

Ta kategoria zawiera składowe naprężeń wynikające z momentów zginających i sił membrany. Odnoszą się one do kierunków lokalnych osi powierzchni. W przypadku powierzchni zakrzywionych odnoszą się do osi elementów skończonych.

Naprężenia zginające i membranowe oznaczają szczegółowo:

σ_{x, b} = \frac{6 m_{x}}{d^{2}}

d	grubość powierzchni

Naprężenie σ_x,b wywołane momentem zginającym m_x

σ_{y, b} = \frac{6 m_{y}}{d^{2}}

Naprężenie σ_y,b wywołane momentem zginającym m_y

τ_{x y, b} = \frac{6 m_{x y}}{d^{2}}

Naprężenie τ_xy,b wywołane momentem skręcającym m_xy

σ_{x, m} = \frac{n_{x}}{d}

Naprężenie membranowe σ_x,m wywołane siłą osiową n_x

σ_{y, m} = \frac{n_{y}}{d}

Naprężenie membranowe σ_y,m wywołane siłą osiową n_y

τ_{x y, m} = \frac{n_{x y}}{d}

Naprężenie τ_{xy, m} wywołane przepływem ścinania n_xy

Naprężenia równoważne

Naprężenia podstawowe są kombinuowane według czterech hipotez naprężeń równoważnych dla stanu naprężenia płaskiego.

Von Mises

Hipoteza według von Mises jest również nazywana "hipotezą energii kształtującej". Opiera się na założeniu, że materiał ulega awarii, gdy energia kształtująca przekracza pewną granicę. Energia kształtująca stanowi energię, która powoduje odkształcenie lub deformację ciała. To podejście jest najczęściej stosowaną hipotezą naprężeń równoważnych. Nadaje się do wszystkich materiałów, które nie są kruche. Ważnym obszarem zastosowań jest konstrukcja stalowa. Hipoteza von Mises nie nadaje się do stanów naprężenia hydrostatycznego z równymi naprężeniami głównymi we wszystkich kierunkach, ponieważ w tym przypadku naprężenie równoważne wynosi zero.

Naprężenia równoważne według von Mises dla stanu naprężenia płaskiego są następujące:

σ_{v, Mises, Max} = \max (σ_{v, Mises, +}; σ_{v, Mises, -})

Maksymalne naprężenie równoważne σ_v,Mises,max na powierzchni dodatniej lub ujemnej

σ_{v, Mises, +} = \sqrt{{σ_{x, +}}^{2} + {σ_{y, +}}^{2} - σ_{x, +} σ_{y, +} + 3 {τ_{x y, +}}^{2}}

Naprężenie równoważne σ_v,Mises,+ po stronie powierzchni dodatniej

σ_{v, Mises, -} = \sqrt{{σ_{x, -}}^{2} + {σ_{y, -}}^{2} - σ_{x, -} σ_{y, -} + 3 {τ_{x y, -}}^{2}}

Naprężenie równoważne σ_v,Mises,- na powierzchni ujemnej

σ_{v, Mises, m} = \sqrt{{σ_{x, m}}^{2} + {σ_{y, m}}^{2} - σ_{x, m} σ_{y, m} + 3 {τ_{x y, m}}^{2}}

Ekwiwalentne naprężenie membranowe σ_v,Mises,m

Tresca

Hipoteza według Tresca jest również znana jako "hipoteza naprężeń ścinających". Zakłada się, że awaria jest spowodowana maksymalnym naprężeniem ścinającym. Ponieważ ta hipoteza jest odpowiednia dla materiałów kruchych, jest często stosowana w inżynierii mechanicznej.

Naprężenia równoważne według Tresca są określane w następujący sposób:

σ_{v, Tresca, Max} = \max (σ_{v, Tresca, +}; σ_{v, Tresca, -})

Maksymalne naprężenie równoważne σ_v,Tresca,max na powierzchni dodatniej lub ujemnej

σ_{v, Tresca, +} = \max (|σ_{1, +} - σ_{2, +}|; |σ_{2, +}|; |σ_{1, +}|) bzw .

σ_{v, Tresca, +} = \max (\sqrt{{(σ_{x, +} - σ_{y, +})}^{2} + 4 {τ_{xy, +}}^{2}}; |σ_{2, +}|; |σ_{1, +}|)

Naprężenie równoważne σ_{v, Tresca, +} po stronie powierzchni dodatniej

σ_{v, Tresca, -} = \max (|σ_{1, -} - σ_{2, -}|; |σ_{2, -}|; |σ_{1, -}|) bzw .

σ_{v, Tresca, -} = \max (\sqrt{{(σ_{x, -} - σ_{y, -})}^{2} + 4 {τ_{xy, -}}^{2}}; |σ_{2, -}|; |σ_{1, -}|)

Naprężenie równoważne σ_v,Tresca,- na powierzchni ujemnej

σ_{v, Tresca, m} = \max (|σ_{1, m} - σ_{2, m}|; |σ_{2, m}|; |σ_{1, m}|) bzw .

σ_{v, Tresca, m} = \max (\sqrt{{(σ_{x, m} - σ_{y, m})}^{2} + 4 {τ_{xy, m}}^{2}}; |σ_{2, m}|; |σ_{1, m}|)

Ekwiwalentne naprężenie membranowe σ_v,Tresca,m

Rankine

Hipoteza naprężenia równoważnego według Rankine jest również znana jako "hipoteza naprężenia normalnego". Zakłada się, że największe naprężenie główne prowadzi do awarii.

Naprężenia równoważne według Rankine są określane w następujący sposób:

σ_{v, Rankine, Max} = \max (σ_{v, Rankine, +}; σ_{v, Rankine, -})

Maksymalne naprężenie równoważne σ_{v, Rankine'a, max} na powierzchni dodatniej lub ujemnej

σ_{v, Rankine, +} = \frac{1}{2} |σ_{x, +} + σ_{y, +}| + \frac{1}{2} \sqrt{{(σ_{x, +} - σ_{y, +})}^{2} + 4 {τ_{xy, +}}^{2}}

Naprężenie równoważne σ_v,Rankine,+ po stronie powierzchni dodatniej

σ_{v, Rankine, -} = \frac{1}{2} |σ_{x, -} + σ_{y, -}| + \frac{1}{2} \sqrt{{(σ_{x, -} - σ_{y, -})}^{2} + 4 {τ_{xy, -}}^{2}}

Naprężenie równoważne σ_v,Rankine'a na ujemnej stronie powierzchni

σ_{v, Rankine, m} = \frac{1}{2} |σ_{x, m} + σ_{y, m}| + \frac{1}{2} \sqrt{{(σ_{x, m} - σ_{y, m})}^{2} + 4 {τ_{xy, m}}^{2}}

Naprężenie równoważne σ_{v, Rankine, m}

Bach

Hipoteza naprężenia równoważnego według Bach jest również znana jako "hipoteza głównego odkształcenia". Zakłada się, że awaria występuje w kierunku największego odkształcenia. To podejście jest podobne do określania naprężenia według Rankine. Zamiast głównego naprężenia używane jest jednak główne odkształcenie.

Naprężenia równoważne według Bach są określane w następujący sposób:

σ_{v, Bach, Max} = \max (σ_{v, Bach, +}; σ_{v, Bach, -})

Maksymalne naprężenie równoważne σ_v,Bach,max na dodatniej lub ujemnej stronie powierzchni

σ_{v, Bach, +} = \max (\frac{1 - ν}{2} |σ_{x, +} + σ_{y, +}| + \frac{1 + ν}{2} \sqrt{{(σ_{x, +} - σ_{y, +})}^{2} + 4 {τ_{xy, +}}^{2}}; ν |σ_{x, +} + σ_{y, +}|)

ν	Querdehnzahl

Naprężenie równoważne σ_v,Bach,+ po stronie powierzchni dodatniej

σ_{v, Bach, -} = \max (\frac{1 - ν}{2} |σ_{x, -} + σ_{y, -}| + \frac{1 + ν}{2} \sqrt{{(σ_{x, -} - σ_{y, -})}^{2} + 4 {τ_{xy, -}}^{2}}; ν |σ_{x, -} + σ_{y, -}|)

Naprężenie równoważne σ_v,Bach,- na powierzchni ujemnej

σ_{v, Bach, m} = \max (\frac{1 - ν}{2} |σ_{x, m} + σ_{y, m}| + \frac{1 + ν}{2} \sqrt{{(σ_{x, m} - σ_{y, m})}^{2} + 4 {τ_{xy, m}}^{2}}; ν |σ_{x, m} + σ_{y, m}|)

Ekwiwalentne naprężenie membranowe σ_v,Bach,m

Rozdział nadrzędny

Wyniki według powierzchni