Obciążenia prętowe to siły, momenty, masy, oddziaływania temperaturowe lub przemieszczenia wymuszone działające na pręty.
Wybierz w liście 'Przypadek obciążenia', do którego ma być przypisane obciążenie.
Podstawowe ustawienia
Karta Podstawowe zarządza podstawowymi parametrami obciążenia.
Kategorie
W liście 'Typ obciążenia' dostępne są następujące opcje:
| Typ obciążenia | Opis |
|---|---|
| Siła | Pojedyncze obciążenie, równomierne lub zmienne obciążenie liniowe |
| Moment | Pojedynczy moment, równomierny lub zmienny moment liniowy |
| Masa | Równomiernie rozłożona masa na długości pręta, istotna dla Analiz dynamicznych |
| Temperatura | Równomierne (Tt = Tb) lub nierównomierne (Tt ≠ Tb) obciążenie temperaturowe rozłożone po przekroju pręta |
| Zmiana temperatury | Różnica temperatur między górną a dolną stroną pręta, ewentualnie z uwzględnieniem stałej zmiany temperatury (dodatnia wartość obciążenia: górna strona pręta podgrzewa się) |
| Zmiana długości | Odkształcenie lub ściskanie ε pręta (dodatnia wartość obciążenia: pręt jest rozciągany) |
| Przesunięcie wzdłużne | Odkształcenie lub ściskanie Δl pręta |
| Podwyższenie | Krzywizna wymuszona pręta |
| Wstępne naprężenie | Siła wstępnego naprężenia działająca na pręt przed obliczeniem (dodatnia wartość obciążenia: pręt jest rozciągany) |
| Przesunięcie | Wymuszone przesunięcie o wartość Δ dla określenia linii wpływu |
| Obrót | Wymuszone obrócenie o kąt φ w odniesieniu do linii wpływu |
| Zawartość rury - pełna | Obciążenie liniowe wynikające z pełnego wypełnienia rury |
| Zawartość rury - częściowa | Obciążenie liniowe wynikające z częściowego wypełnienia rury |
| Ciśnienie wewnętrzne rury | Równomierne ciśnienie wewnętrzne w rurze |
| Ruch obrotowy | Siła odśrodkowa wynikająca z masy i prędkości kątowej ω na pręcie |
| Naprężenie końcowe | Siła wstępnego naprężenia, która po obliczeniach ma być obecna w pręcie przy użyciu iteracyjnego określenia (dodatnia wartość obciążenia: pręt w stanie naprężenia) |
| Otulina - kontur | Siła wynikająca z ciężaru materiału o określonej grubości na zarys przekroju (lód, farba) |
| Otulina - wielokąt | Siła wynikająca z ciężaru materiału otaczającego przekrój w swobodnie definiowalnym obszarze (obudowa przeciwpożarowa) |
| Wyszukiwanie kształtu (tylko dla dodatku Znajdowanie kształtu) | Jednorodna siła lub specyfikacja geometryczna dla obciążenia wyszukiwania kształtu (zobacz rozdział Obciążenia wyszukiwania kształtu podręcznika wyszukiwania kształtu) |
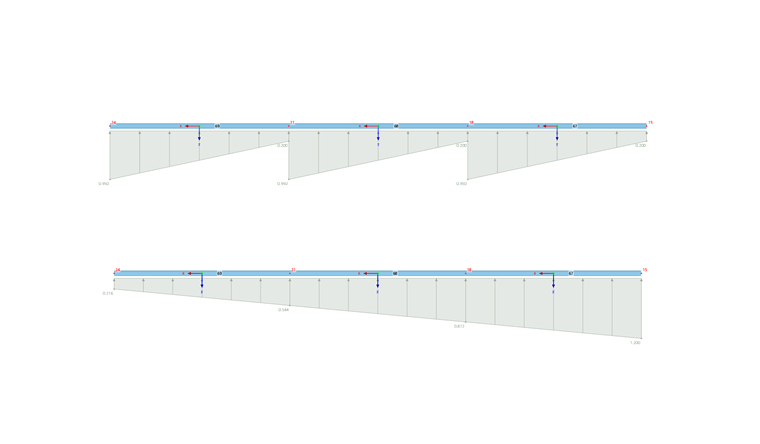
Typ obciążenia i działanie znaków wyjaśniono na górnym rysunku dialogu.
W liście 'Rozkład obciążenia' dostępne są różne możliwości wyboru, aby odwzorować rozkład obciążenia.
Schemat rozkładu obciążenia jest zobrazowany na górnym rysunku dialogu. W sekcji 'Parametry' można następnie określić wartości, odstępy i inne cechy charakterystyczne obciążenia.
Wybierz w liście 'Układ współrzędnych', czy obciążenie działa w kierunku lokalnych osi pręta xyz, lokalnych osi głównych xuv, czy globalnych osi XYZ. Alternatywnie, możesz wybrać lub utworzyć nowy niestandardowy układ współrzędnych.
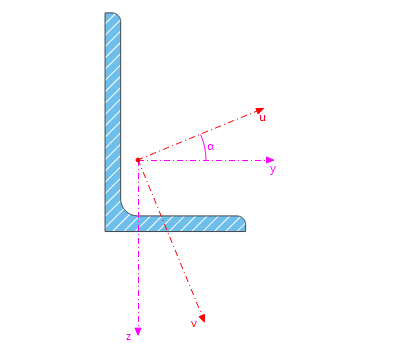
Lokalna oś x reprezentuje oś wzdłużną pręta. Dla profilów symetrycznych, oś y to oś "silna" przekroju pręta, oś z to oś "słaba". W przypadku profili niesymetrycznych są to odpowiednio osie u i v.
Wybierz w liście 'Kierunek obciążenia', aby określić działanie obciążenia. W zależności od układu współrzędnych, do wyboru są lokalne osie pręta x, y, z, główne osie x, u, v, globalne osie X, Y, Z lub osie niestandardowe U, V, W.
Obciążenie prętowe może być odniesione do rzeczywistej długości (jak obciążenie ciężarem) lub do długości projecjonalnej (jak obciążenie śniegiem). Kierunek obciążenia jest zobrazowany na szkicu dialogowym.
Parametry
Wprowadź wartość obciążenia dla siły, momentu lub masy. Dla obciążeń punktowych lub zmiennych dostępne jest kilka pól wprowadzania, w których można opisać obciążenie prętowe. Znaczenie parametrów jest zobrazowane na szkicu obciążenia.
Dodatni moment działa prawoskrętnie wokół odpowiedniej osi dodatniej. Globalny układ osi w oknie roboczym pomoże Ci w ustaleniu znaku. Dla lokalnie zdefiniowanych obciążeń, możesz zobrazować osie pręta przyciskiem
(zobacz obraz Zmienne obciążenie prętowe).
Jeśli definiujesz obciążenia punktowe lub trapezowe, możesz przyciskiem
przełączać się między względnym a absolutnym wprowadzeniem odległości.
Dla obciążeń zmiennych wyświetlana jest tabela, w której możesz określić miejsca obciążenia x z odpowiadającymi im wartościami obciążeń.
Opcje
Zazwyczaj obciążenie działa niezależnie na każdy z prętów, które określisz w sekcji 'Przypisane do prętów'. Jeżeli zaznaczysz pole wyboru 'Odniesienie do listy prętów', obciążenie prętowe będzie działało na całkowitą długość prętów: dla obciążeń trapezowych RFEM nie przypisuje parametrów do każdego pręta, ale jako całość do wszystkich prętów na liście.
Pole wyboru 'Odniesienie odstępów do końców prętów' jest dostępne tylko dla obciążeń, które nie działają na całkowitą długość linii. Po jego zaznaczeniu możesz określić odległości w sekcji 'Parametry' w odniesieniu do końca pręta.
Pole wyboru 'Obciążenie na całkowitej długości pręta' umożliwia kontrolę, czy zmienne liniowe obciążenie trapezowe jest umieszczane przez cały czas, od początku do końca pręta.
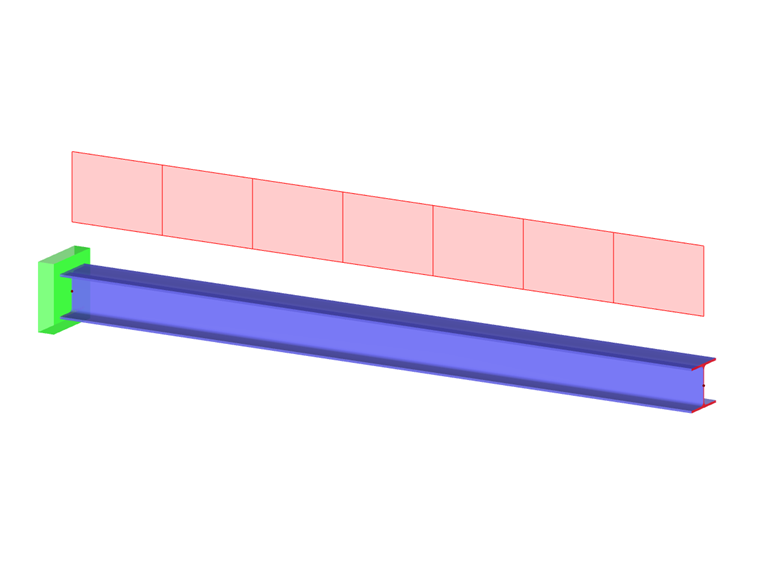
Pole wyboru 'Ekscentryczność' jest dostępne dla typu obciążenia 'Siła'. Po jego zaznaczeniu możesz w karcie Ekscentryczność siły zdefiniować ekscentryczne działanie obciążenia prętowego.
Pole wyboru 'Przejęcie reakcji podpór' umożliwia importowanie sił podporowych z innego modelu. Możesz następnie wprowadzić informacje w dodatkowej karcie (zobacz obraz Model, Obciążenie i linia do określenia dla importu reakcji podpory).
Opcja 'Wyświetlanie po stronie przeciwnej' pozwala kontrolować wyświetlanie wektorów obciążenia.
Ekscentryczność siły
Jeśli siła nie działa w środku sprężystości przekroju, możesz określić miejsce przyłożenia obciążenia w zakładce Ekscentryczność siły.
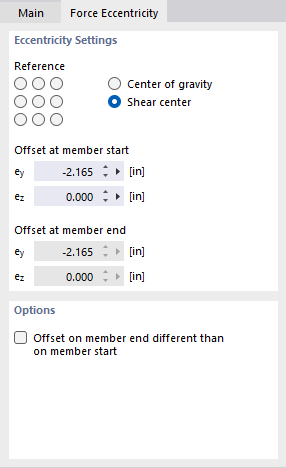
Ustawienia ekscentryczności
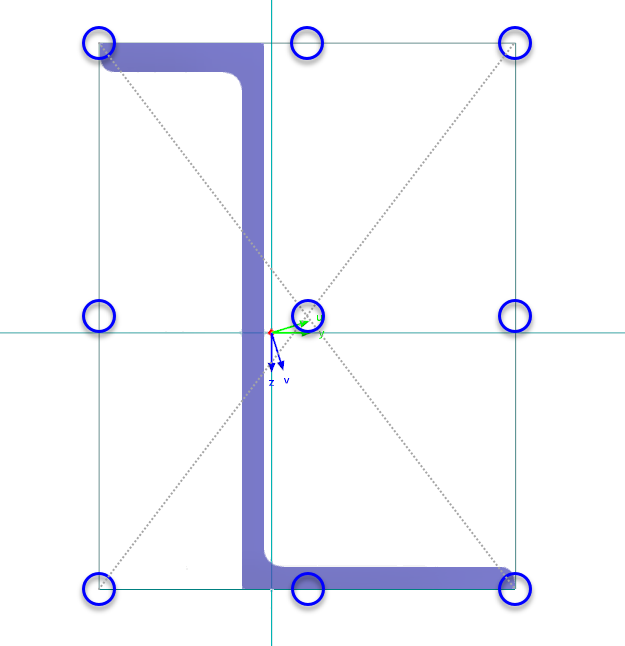
Dziewięć pól wyboru 'Odniesienie' symbolizuje charakterystyczne punkty na przekroju: punkt środkowy reprezentuje geometryczny środek prostokąta otaczającego przekrój. Osiem punktów brzegowych wynika z przecięcia równoległych osi pręta y i z przez ten środek z liniami brzegowymi prostokąta. Po aktywowaniu jednego z pól, RFEM przypisuje obciążenie prętowe w odpowiedniej odległości od środka ciężkości.
Alternatywnie, można przyłożyć obciążenie w 'Środku ciężkości' lub 'Środku ścinania' i ręcznie zdefiniować przesunięcie na początku pręta w polach wpisu poniżej. Odległości odnoszą się do lokalnych osi pręta y i z.
Opcje
Jeżeli nie występuje równomierna ekscentryczność wzdłuż pręta, zaznacz pole 'Przesunięcie na końcu pręta inne niż na początku pręta'. Możesz wtedy określić przesunięcie na końcu pręta w sekcji powyżej. W ten sposób można opisać liniowy przebieg ekscentryczności od początku do końca pręta.
