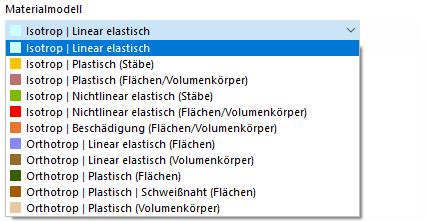
Modele materiałowe
Jeśli w Parametry podstawowe modelu aktywowano rozszerzenie obliczeń Nieliniowe zachowanie materiału (wymagana licencja), oprócz modeli materiałowych 'Izotropowy | Liniowo sprężysty' i 'Ortotropowy | Liniowo sprężysty' dostępne są inne opcje.
Procedury obliczeniowe
Jeśli zastosowano nieliniowy model materiałowy, zawsze przeprowadzane jest obliczenie iteracyjne. W zależności od modelu materiałowego definiowany jest różny związek między naprężeniami a odkształceniami.
Sztywność elementów skończonych jest dostosowywana w trakcie iteracji, aż do spełnienia zależności naprężenie-odkształcenie. Dostosowanie odbywa się zawsze dla całego elementu powierzchniowego lub wolumetrycznego. Dlatego przy ocenie naprężeń zawsze powinna być stosowana metoda wygładzania Stała w elementach siatki.
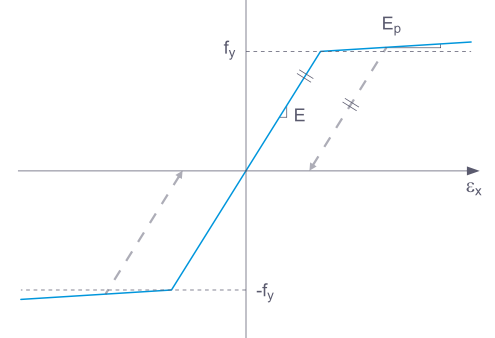
Niektóre modele materiałowe w RFEM są oznaczone jako 'plastyczne', inne jako 'nieliniowo sprężyste'. Jeśli element z materiałem nieliniowo sprężystym jest odciążany, odkształcenie powraca tą samą drogą. Przy pełnym odciążeniu nie pozostaje żadne odkształcenie.
Przy odciążaniu elementu z modelem materiałowym plastycznym po pełnym odciążeniu pozostaje pewne odkształcenie.
Załadunek i odciążenie można symulować za pomocą rozszerzenia Analiza etapów budowy.
Informacje na temat nieliniowych modeli materiałowych można znaleźć w artykule technicznym Modele plastyczne w modelu materiału Izotropowy nieliniowo sprężysty.
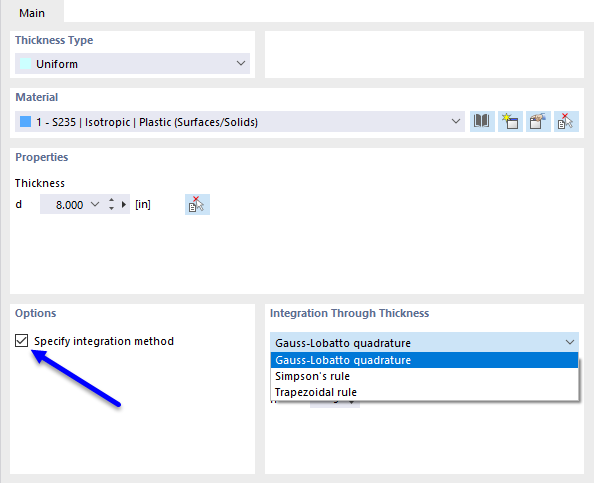
Siły we wnętrzu płyt z nieliniowym materiałem wynikają z numerycznej integracji naprężeń przez grubość płyty. Aby ustawić metodę integracji na grubość, w dialogu 'Edycja grubości' zaznacz opcję Określ metodę integracji. Dostępne są następujące metody integracji:
- Kwadratura Gaussa-Lobatto
- Reguła Simpsona
- Reguła trapezów
Dodatkowo można określić 'Liczbę punktów integracji' przez grubość płyty od 3 do 99.
Izotropowy plastyczny (Pręty)
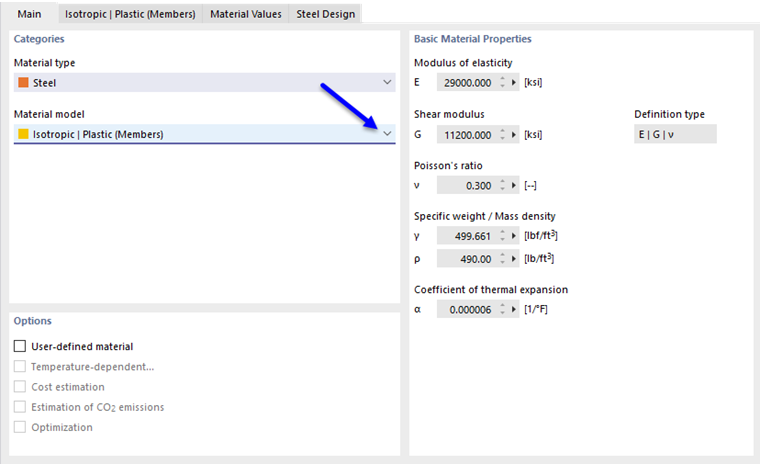
Jeśli w rozwijanej liście 'Model materiału' wybrać wartość Izotropowy | Plastyczny (Pręty), aktywna staje się karta do wprowadzania nieliniowych parametrów materiałowych.
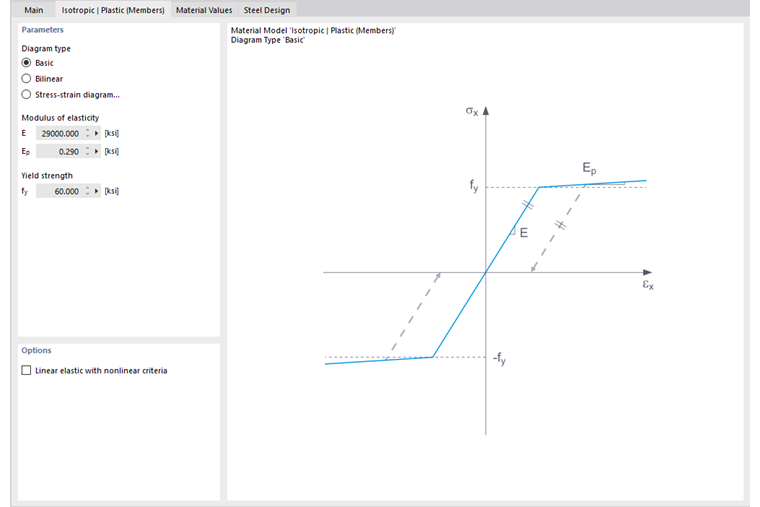
W tej karcie definiujesz diagram naprężenie-odkształcenie. Dostępne są następujące opcje:
- Standard
- Dwuliniowy
- Diagram
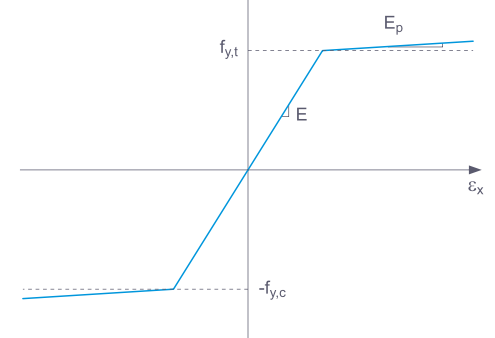
Jeśli wybrano Standard, RFEM używa dwuliniowego modelu materiałowego. Wartości modułu Younga E i granicy plastyczności fy są pobierane z bazy danych materiałów. Ze względów numerycznych gałąź nie przebiega dokładnie poziomo, ale ma mały wzrost Ep.
Jeśli chcesz zmienić wartości granicy plastyczności i modułu Younga, aktywuj pole wyboru Niestandardowy materiał w karcie 'Podstawowe'.
W definicji dwuliniowej można również wprowadzić wartość Ep.
Bardziej złożone relacje między naprężeniem a odkształceniem można zdefiniować za pomocą Diagramu naprężenie-odkształcenie. Gdy wybierzesz tę opcję, wyświetlana jest karta 'Diagram naprężenie-odkształcenie'.
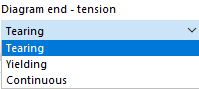
W każdej linii zdefiniuj punkt dla relacji naprężenie-odkształcenie. Jak diagram powinien kontynuować się po ostatnim punkcie definicji, można wybrać w liście 'Koniec diagramu' poniżej diagramu:
W przypadku 'Pęknięcia' naprężenie spada do zera po ostatnim punkcie definicji. 'Cieknie' oznacza, że naprężenie pozostaje stałe przy rosnącym odkształceniu. 'Ciągły' oznacza, że krzywa kontynuuje się z nachyleniem ostatniego odcinka.
Izotropowy plastyczny (Powierzchnie/Woluminy)
Jeśli w rozwijanej liście 'Model materiału' wybrany zostanie wpis Izotropowy | Plastyczny (Powierzchnie/Woluminy), aktywna staje się karta do wprowadzania nieliniowych parametrów materiałowych.
Najpierw wybierz 'Hipotezę wytrzymałościową'. Hipotezy do wyboru:
- von Mises (hipoteza energii odkształcenia kształtu)
- Tresca (hipoteza naprężenia ścinającego)
- Drucker-Prager
- Mohr-Coulomb
Jeśli wybierzesz von Mises, w diagramie naprężenie-odkształcenie używane są następujące naprężenia:
- Powierzchnie
- Woluminy
Według hipotezy Tresca stosowane są te naprężenia:
- Powierzchnie
- Woluminy
Według hipotezy Drucker-Prager to naprężenie jest stosowane dla powierzchni i woluminów:
|
σc |
Naprężenie graniczne w ściskaniu |
|
σt |
Naprężenie graniczne dla rozciąganie |
Według hipotezy Mohr-Coulomb stosowane jest to naprężenie dla powierzchni i woluminów:
Izotropowy nieliniowo sprężysty (Pręty)
Zasada działania jest zbliżona do modelu materiału Izotropowy plastyczny (Pręty). W przeciwieństwie do tego nie pozostaje jednak po odciążeniu żadne odkształcenie plastyczne.
Izotropowy nieliniowo sprężysty (Powierzchnie/Woluminy)
Zasada działania jest bliska modelowi materiału Izotropowy plastyczny (Powierzchnie/Woluminy). W odróżnieniu od tego nie pozostaje jednak po odciążeniu żadne odkształcenie plastyczne.
Izotropowy uszkodzenie (Powierzchnie/Woluminy)
W przeciwieństwie do innych modeli materiałowych diagram naprężenie-odkształcenie dla tego modelu materiałowego nie jest symetryczny względem początku układu współrzędnych. Dzięki temu można za pomocą tego modelu materiałowego odwzorować zachowanie betonu włóknistego. Szczegółowe informacje na temat modelowania betonu włóknistego można znaleźć w artykule technicznym Właściwości materiałowe betonu włóknistego.
Izotropowa sztywność jest zmniejszana za pomocą skalarnie określonego parametru uszkodzenia. Ten parametr uszkodzenia wynika z przebiegu naprężenia określonego w diagramie. Nie jest rozpatrywany kierunek głównych naprężeń, lecz uszkodzenie będzie w kierunku uśrednionego odkształcenia, które uwzględnia także trzecią orientację prostopadłą do płaszczyzny. Obszar rozciągania i ściskania tensora naprężenia jest traktowany osobno, co oznacza, że stosowane są różne parametry uszkodzenia.
'Rozmiar elementu odniesienia' określa, jak odkształcenie jest skalowane na długość elementu w obszarze pęknięć. Przy domyślnej wartości zero nie ma skalowania. Dzięki temu realnie odwzorowane jest zachowanie betonu włóknistego.
Teoretyczne tło modelu materiałowego 'Izotropowe uszkodzenie' można znaleźć w artykule technicznym Nieliniowy model materiałowy Uszkodzenie.
Ortotropowy plastyczny (Powierzchnie) / Ortotropowy plastyczny (Woluminy)
Model materiału według Tsai-Wu łączy właściwości plastyczne i ortotropowe. Dzięki temu możliwe jest specjalne modelowanie materiałów o anizotropowej charakterystyce, takich jak kompozyty włókniste lub drewno.
Podczas plastycznej deformacji materiału naprężenia pozostają stałe. Następuje ich redystrybucja zależna od sztywności, które są dostępne w poszczególnych kierunkach.
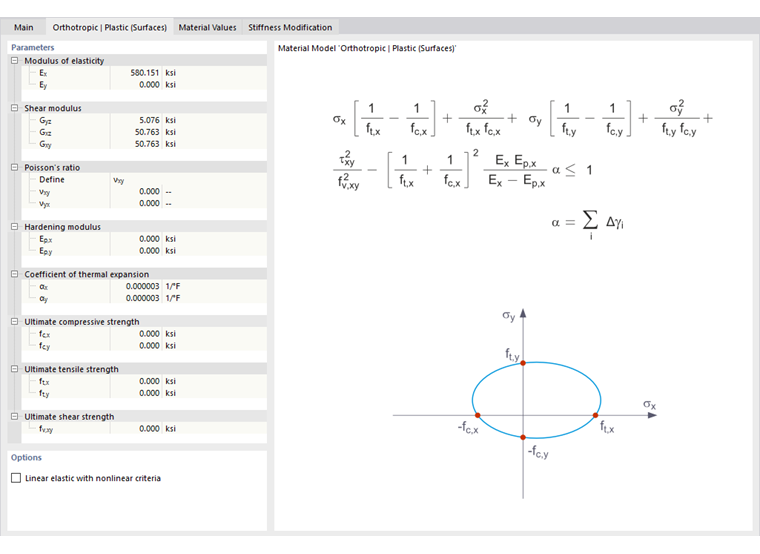
Obszar sprężysty odpowiada modelowi materiałowemu Ortotropowy liniowo sprężysty (Woluminy). Dla obszaru plastycznego obowiązuje następujące równanie plastyczności wg Tsai-Wu:
- Powierzchnie
- Woluminy
Wszelkie wytrzymałości należy określić jako wartości dodatnie.
Równanie plastyczności można sobie wyobrazić jako eliptyczną powierzchnię w sześciowymiarowej przestrzeni naprężeń. Jeśli jedna z trzech składowych naprężenia jest stałą wartością, powierzchnię można rzutować na trójwymiarową przestrzeń naprężeń.
Jeśli wartość dla fy(σ) według równania Tsai-Wu, stan naprężenia w płaszczyźnie jest mniejsza niż 1, naprężenia znajdują się w obszarze sprężystym. Obszar plastyczny jest osiągany, gdy fy(σ) = 1. Wartości większe niż 1 są niedopuszczalne. Model zachowuje się idealnie plastycznie, to znaczy nie występuje utwardzenie.
Ortotropowy plastyczny spoiny (Powierzchnie)
Ten model materiałowy jest używany w analizach z rozszerzeniem Złącza stalowe, aby prawidłowo odwzorować zachowanie spoin zgodnie z normami. Na powierzchni zastępczej powstają naprężenia jedynie odpowiednie do naprężeniowych składowych σ⊥, τ⊥ i τ|| spoiny. W pozostałych kierunkach naprężeń sztywność powierzchni zastępczej dąży do zera.
W zakładce 'Ortotropowy | Plastyczny | Spoiny (Powierzchnie)' można określić parametry uwzględnienia plastycznej progresji materiałowej w spoinach, na przykład granice fekv i fx do sprawdzenia naprężeń według 'metody kierunkowej' zgodnie z EN 1993-1-8 [1] dla spoin, zmodyfikowane o plastyczną część (zobacz także artykuł techniczny Sprawdzanie spoin pachwinowych).
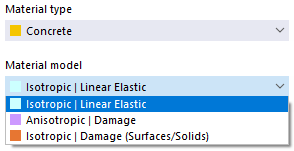
Beton
Dla typu materiału 'Beton' dostępne są nieliniowe modele materiałowe 'Anizotropowy | Uszkodzenie' oraz 'Izotropowy | Uszkodzenie (Powierzchnie/Woluminy)'.
Te modele materiałowe są opisane w rozdziale Anizotropowy | Uszkodzenie podręcznika betonowego oraz powyżej w sekcji Izotropowy Uszkodzenie.
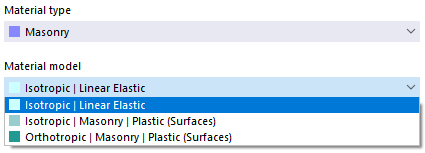
Cegła
Jeśli w Parametry podstawowe modelu aktywowano rozszerzenie projektowe Projektowanie murów (wymagana licencja), dla typu materiału 'Cegła' dostępne są nieliniowe modele materiałowe 'Izotropowy | Cegła | Plastyczny (Powierzchnie)' oraz 'Ortotropowy | Cegła | Plastyczny (Powierzchnie)'.
Oba modele materiałowe są opisane w rozdziale Materiały podręcznika projektowania murów.